部分截图来自原课程视频《2023李宏毅最新生成式AI教程》，B站自行搜索

这节课主要是复习，但是里面有些结论可以加深对ML和DL的理解。

机器学习的本质

让机器自动寻找 计算出一个函数，这个函数能完成我们既定的目标。例如：
ChatGPT是找一个函数能够完成下一个字/词的预测。

Midjourney是找一个函数根据文字内容生成对应图片。（PS：中间有一节课是用ChatGPT+Midjourney玩虚拟冒险游戏，演示为主）

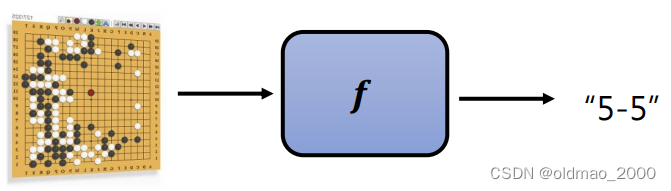
AlphaGo是找一个函数根据当前棋局预测下一步落子位置。

机器学习的类型

Regression/回归

函数输出为一个数值。典型的任务有NG的房价预测、这个前导课中的PM2.5预测等。

Classification/分类

函数输出为一个类别。典型任务有，垃圾邮件识别、银行贷款审批、手写数字识别等。

Structured Learning/结构化学习

函数的输出是有结构的物件（影像、图片、文字、声音等）
这个类别不属于上面两类传统机器学习的分类，这个类别更加复杂。Structured Learning发展到今天也有了更潮的称呼：Generative Learning生成式学习。Structured Learning在早期李宏毅的机器学习课程中是单独的一个部分。

对于ChatGPT而言，在微观上，每一次预测下一个字/词，相当于在做分类任务，只不过类别就是我们的词库中所有的字/词；在宏观上，当我们使用ChatGPT的时候，他一次会输出一段文字，又可以看成是生成式的学习。

结论：ChatGPT是把生成式学习拆解成多个分类问题来解决。

ML的三板斧

看到这里又梦回20年刷到机器学习课程的时候，可惜一直没有玩过宝可梦游戏，不然理解会更加深刻。
不过这次回顾讲解更加精简明的描述了机器学习找到梦中情function的过程。

前提
开始之前要决定找什么样的函数。这是一个与技术无关的问题，就是根据需要定下来函数是属于上面三种类型的哪一类，下面以回归为例，吃图片预测其战斗力数值。

设定范围

设定范围就是选定Model（候选函数的集合）。
DL中的各种模型结构（CNN，RNN，Transformer等）或者各种决策树、感知机等都是各种不同的候选函数的集合。例如我们选定某个结构后，使用四种不同的参数，对于相同的输入，就可以得到不同的结果：

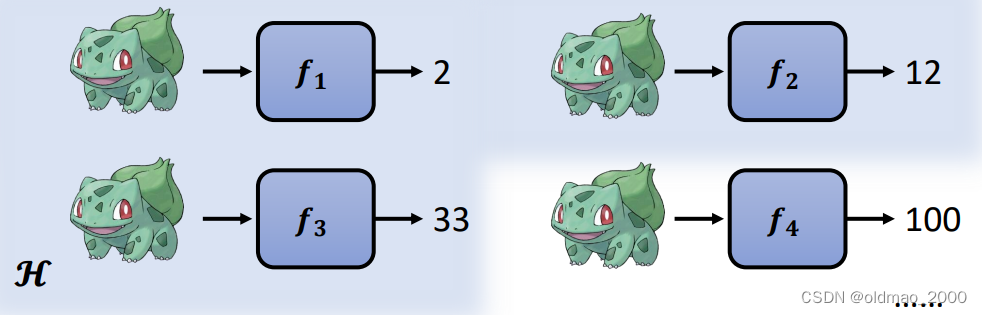
当然参数有无数种可能，我们把某个DL模型的不同参数所形成的函数集合记为：$\mathcal{H}$
这里涉及到函数空间等原理，需要了解的可以看之前的课程。

设定标准

设定Loss（评价函数好坏的标准），以宝可梦战斗力预测任务来举例。现假设有一个函数$f_1$，对三只宝可梦进行预测结果如下：

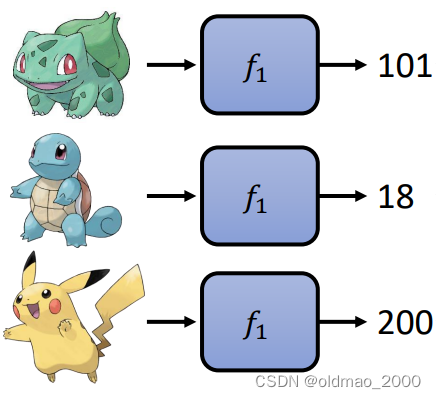
然后根据数据标记方式不同，又分两种情况进行讨论：

监督学习

此时有专业人员对宝可梦实际战斗力进行标注：

此时我们可以对函数$f_1$计算结果的正确程度进行计算Loss：
$$L(f_1)=|103-101|+|17-18|+|212-200|=2+1+12=15$$
PS：$L$称为损失函数，上面宝可梦的战斗力称为训练数据。这里为了简单就直接算，实操会更加复杂，要根据具体训练数据来拟定损失函数，例如是否要加正则项、是否对差值进行平方等。

半监督学习

此时只有部分宝可梦的战斗力得到标注，例如下面只有一只有标注，其他没有：

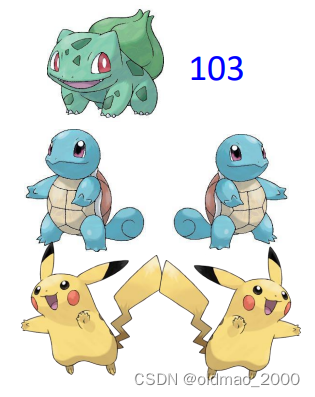
对于有标注的数据，可以按监督学习的方法进行计算Loss，对于其他可以自己制定相应规则，例如：规定外形相似的宝可梦战斗力应该一致。
但是$f_1$函数对于两个皮卡丘的输出如下：

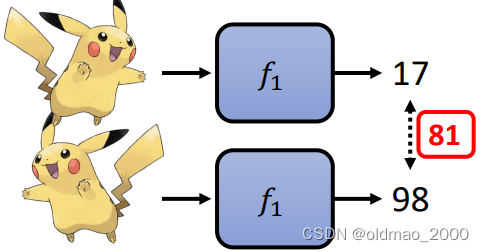
二者差异为81，因此可以得到$f_1$函数的Loss为：
$$L(f_1)=|103-101|+98-17=83$$
当然规则是人定的，也可以定相同颜色的宝可梦战斗力一样。。。
如何定规则？当然也是要根据训练数据来。

其他

当然还有其他中训练方式，例如：强化学习，无监督学习

达成目标

找到最优的函数（Optimization），自觉上，当然是Loss最小的那个函数就是最优：
$$f^{\ast }=arg\underset{f\in \mathcal{H}}{\min }L(f)$$
例如：

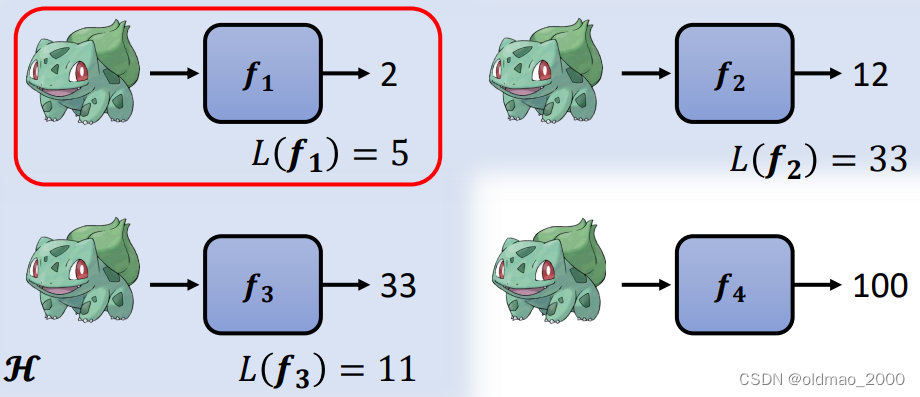
当然具体实作中找最优函数可以看做求Loss最小值的过程，由于Loss函数通常是多项式，那么找到多项式最小值常用的方法就是GD，而对于DL而言，BP就是正解。当然还有类似遗传算法等其他方法可以找到最优函数。

小结

步骤	含义	方法
设定范围	选定候选函数的集合	DL(CNN, RNN, Transformer), Decision Tree, Perceptron, etc.
设定标准	选定评价函数好坏的标准	Supervised Learning, Semi-supervised Learning, Unsupervised Learning, RL, etc.
达成目标	找到最优的函数	Gradient Descent(Adam, AdamW…), Back Propagation, Genetic Algorithm, etc.

好好看上面的表格可以更加深入理解很多概念，例如：RL会取代DL，这个说法是不正确的，两个方法属于不同的步骤，谈不上谁取代谁。
还可以在写论文的时候从不同的出发点来寻找创新idea。
这里有把三个步骤从后往前重新分析了一遍。

达成目标

可以把大大的长方形看做是一个函数，这个函数吃候选函数集合$\mathcal{H}$和评定函数$L$得到一个函数$f^{\ast }$，该函数属于$\mathcal{H}$，并且可以使得$L$的值越小越好（这里不是最小，因为可能是局部最小值）
当然，这个长方形函数比较复杂，需要我们预先设定一些超参数（Hyperparameter）：Learning Rate、Batch Size、How to Init。当然我们也希望长方形函数的鲁棒性很强，对这些超参数不这么敏感。

设定标准

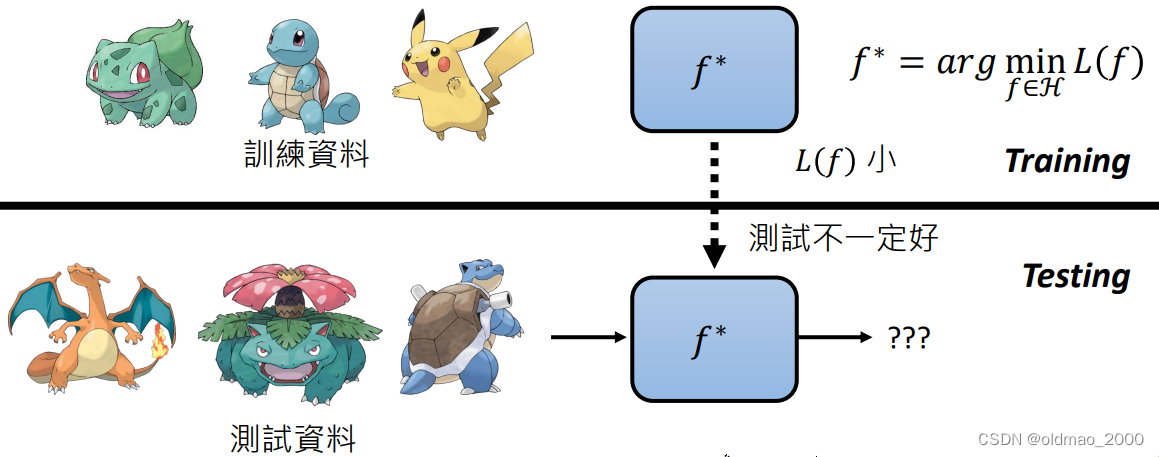
从训练数据中根据评定函数$L$找出$f^{\ast }$，当然在训练数据上表现比较好的$f^{\ast }$在测试数据上表现不一定好，这可能是因为训练数据与测试数据不是相同分布的。
我们可以在训练阶段在评定函数$L$中加入额外考量：正则化。（就好比平时练习使用难度较高的卷子，考试题目虽然没有见过也大概率拿高分）

设定范围

为什么要设定候选函数的范围，而不把覆盖所有向量空间的函数作为我们的范围呢？因为有些函数训练结果好但测试效果差（过拟合）。

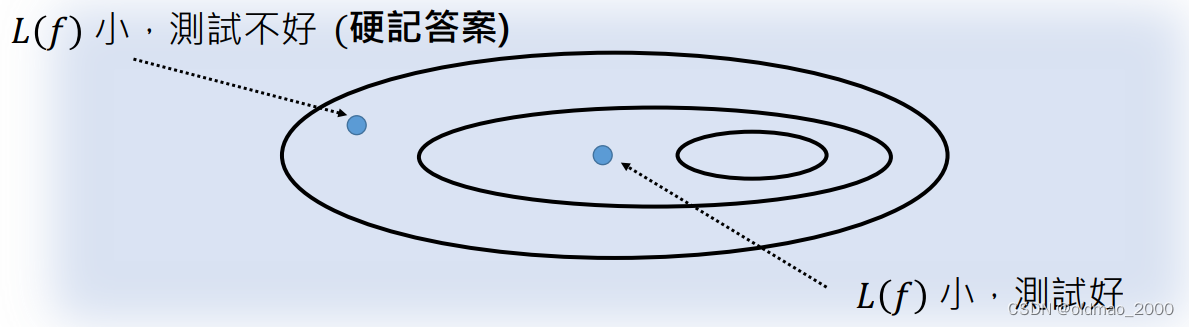
因此我们要划定范围将那些容易过拟合的函数排除在外。当我们设定范围太大就会将过拟合的函数包含进来（最大椭圆），如果设定范围太小，又会将正好拟合的函数排除在外（最小椭圆）。
主要还是根据数据量来看，数据量大，范围可以大一些，例如在图像上的研究趋势看，早期数据量小，因此采用CNN结构，后来数据量变大后，就开始引入Transformer结构，Transformer结构的范围正是要比CNN结构的范围大。

还有一些特殊的方法，例如下图中残差网络，虽然这个结构包含的范围可能不咋地，但是这个结构很容易找出$f^{\ast }$

同理，在损失函数上，使用交叉熵比使用平方差的方式要更容易达成目标。