快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中
的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右
子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
if(right - left <= 1)
return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分
int div = partion(array, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
// 递归排[left, div)
QuickSort(array, left, div);
// 递归排[div+1, right)
QuickSort(array, div+1, right);
}
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉
树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有:
1. hoare版本

看懂了动图那么我们的代码实现如下
// Hoare
int PartSort1(int* a, int left, int right)
{
//int midi = GetMidi(a, left, right);
//Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right)
{
// 找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// 找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
// 三数取中
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
// left mid right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
2.挖坑法

代码实现如下
// 挖坑法
int PartSort2(int* a, int left, int right)
{
int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);
int key = a[left];
// 保存key值以后,左边形成第一个坑
int hole = left;
while (left < right)
{
// 右边先走,找小,填到左边的坑,右边形成新的坑位
while (left < right && a[right] >= key)
{
--right;
}
a[hole] = a[right];
hole = right;
// 左边再走,找大,填到右边的坑,左边形成新的坑位
while (left < right && a[left] <= key)
{
++left;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
// 三数取中
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
// left mid right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
3.前后指针版本

代码实现如下
// 前后指针
int PartSort3(int* a, int left, int right)
{
int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
// 三数取中
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
// left mid right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
2.3.2 快速排序优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序

快速排序的特性总结: - 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
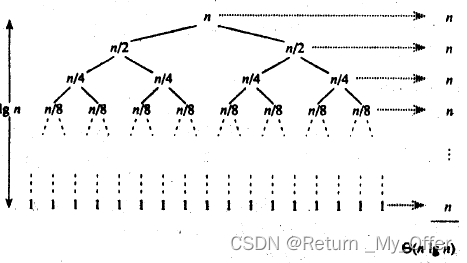
- 空间复杂度:O(logN)
- 稳定性:不稳定

三路划分与三数随机取中的思想实现快速排序的再优化
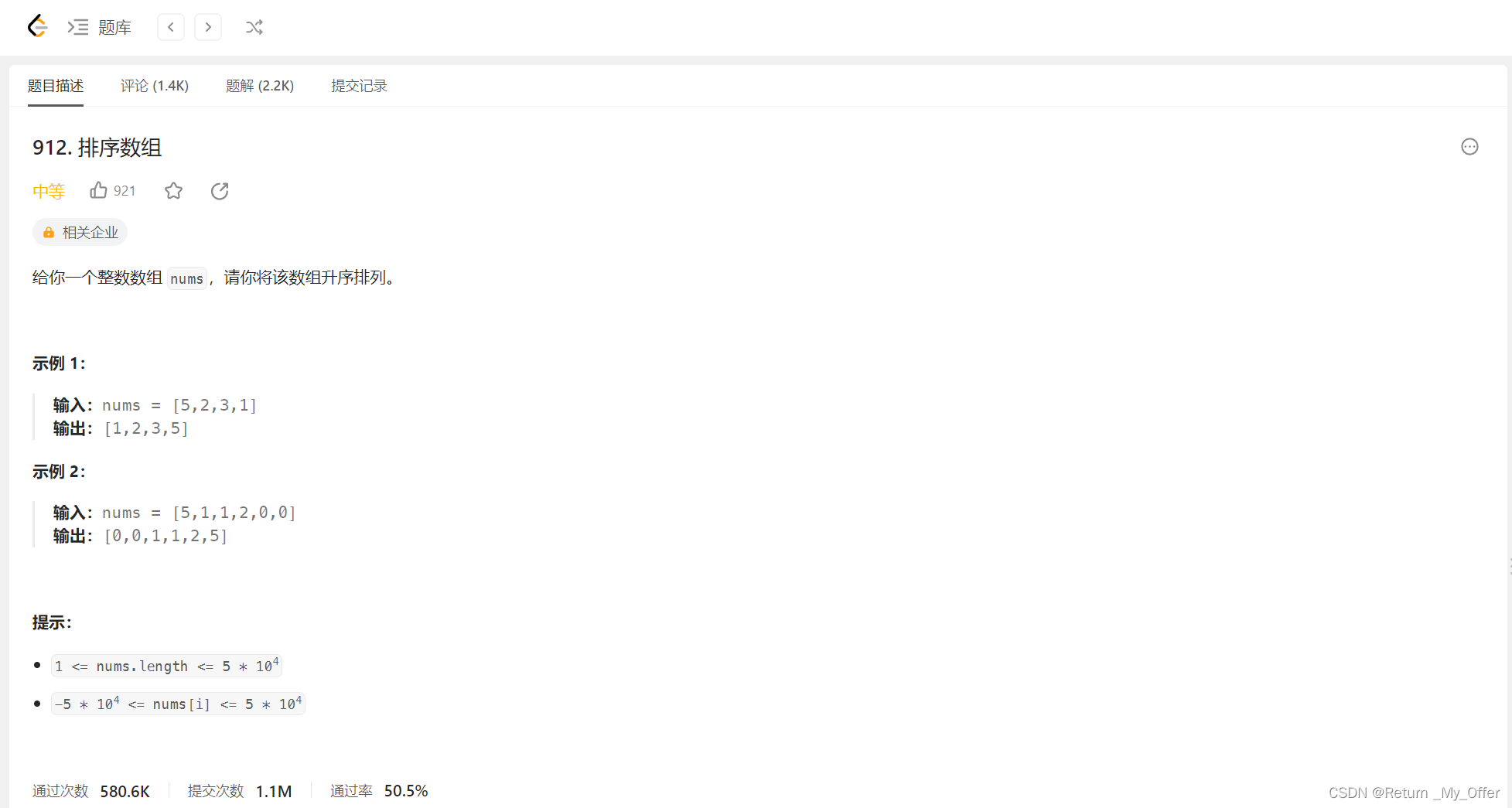
这是题目 我们按照上面所讲的(这里我们使用快速排序的方法来实现 所以代码可以拷贝粘贴 所以我们就不再继续赘述)

看一下这个图片 我们定义一个变量将key保存起来以便后续比较不会丢失key的数据
定义一个cur表示当前数据 然后根据我的蓝色字体部分思考一下 ++L,–R的各自的含义
最后就会形成一个左边为小于key的数 中间为等于key的数 右边为大于key的数 这样做的好处是如果避免大量的重复数据带来的不利影响 希望大家能够理解
这样以来 我们中间的和key相等的数据就不用再次递归了 只用递归左和右的两组数据了 是不是很方便
但是这里还有一个问题就是三数取中我们还要再次优化一下避免Leetcode判题太严格导致我们所有测试用例通过了 但是超时了
下面给大家看一下详细代码和报错示例
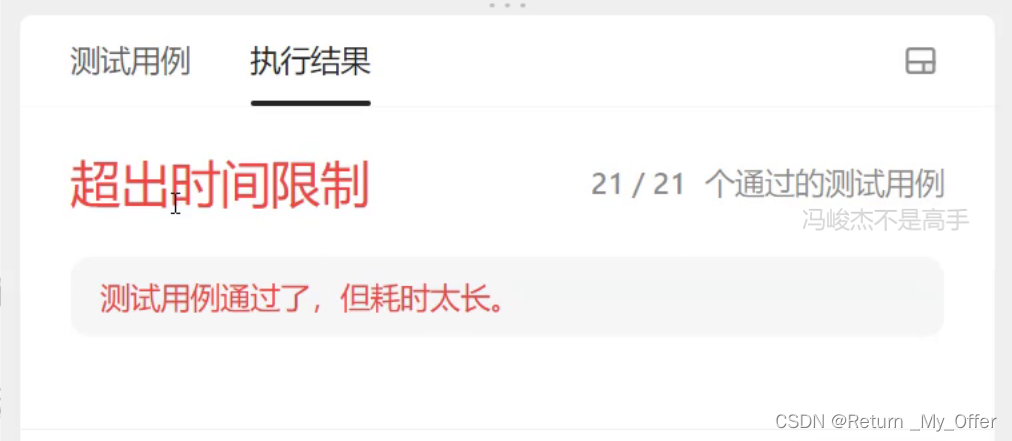

希望我的讲解能够最大限度的帮助到你 希望你今天收获满满 我们下一篇文章再见!


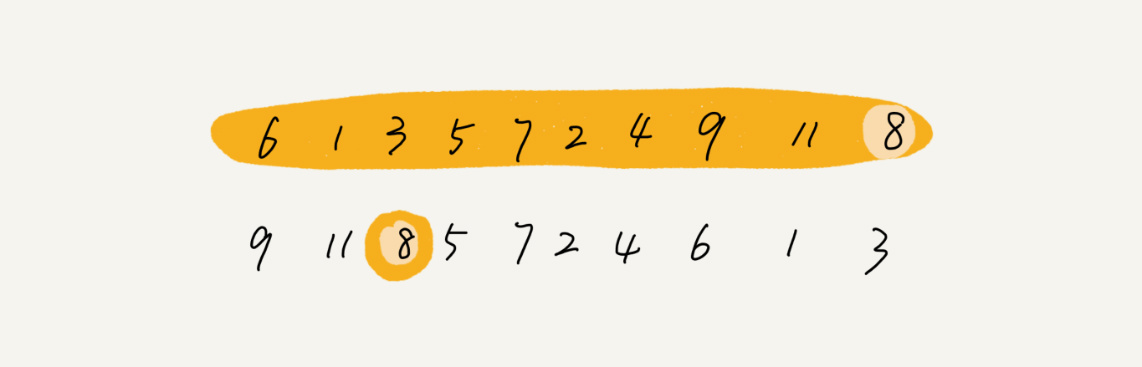


![[产品体验] GPT4识图功能](https://img-blog.csdnimg.cn/14742de352864a6db67deef077f8a0ea.png)