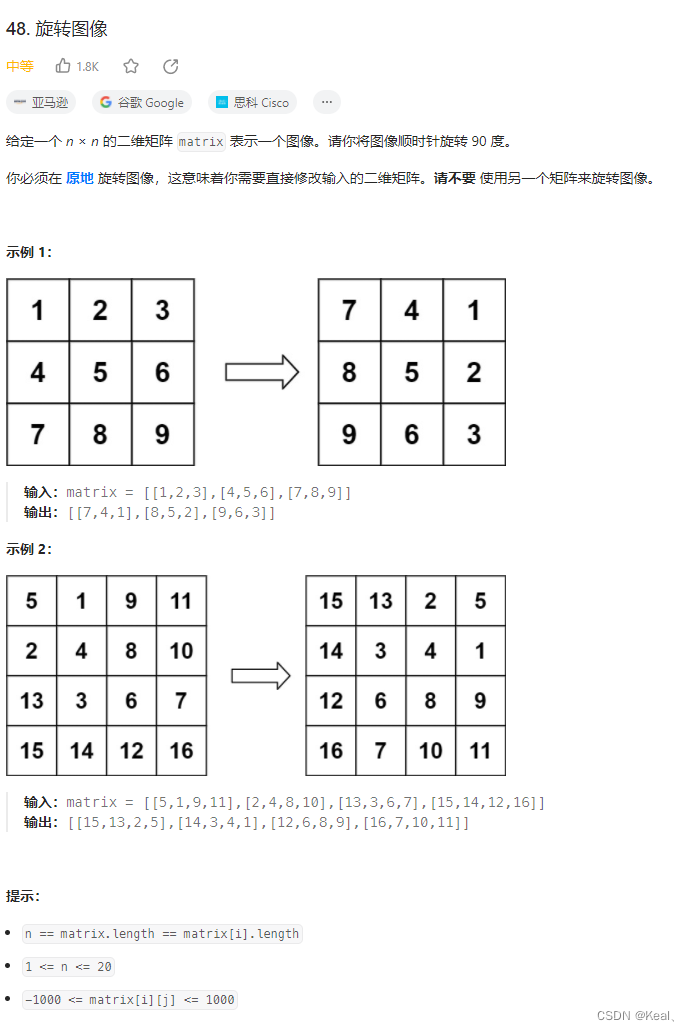
题目：

思路：
第一种思路：使用额外二维矩阵，变化后的直接存入额外的矩阵，不符合题意
以示例2中，第3行，第1列的13为例，旋转后，变为了第1行，第2列
旋转90 后行的位置，变为：原列序号
旋转90 后列的位置，变为：n-原行的位置+1

第二种思路：使用翻转代替旋转

注：掌握技巧后，代码不易出错

代码：

public void rotate(int[][] matrix) {

    int rows = matrix.length;
    int columns = matrix[0].length;

    // 先翻转行
    for (int i = 0; i < rows / 2; i++) {
        for (int j = 0; j < columns; j++) {
            int temp = matrix[rows - i - 1][j];
            matrix[rows - i - 1][j] = matrix[i][j];
            matrix[i][j] = temp;
        }
    }

    // 沿主对角线翻转
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < i; j++) {  // 这里要注意，如果每个元素都翻转，最后又转回来了，沿主对角线，一行一列，两行两列，三行三列，column <= rows 对角线不用换，column < row
            int temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }

}