基于正交对立学习的改进麻雀搜索算法

摘要：针对麻雀搜索算法种群多样性少，局部搜索能力弱的问题，本文提出了基于正交对立学习的改进型麻雀搜索算法（OOLSSA）。首先，在算法中引入正态变异算子，丰富算法种群多样性；其次，利用对立学习策略，增强算法跳出局部最优的能力；然后，在加入者更新之后引入正交对立学习机制，加快算法的收敛速度；

1.麻雀优化算法

基础麻雀算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/108830958

2. 改进麻雀算法

2.1 正态变异扰动

在其原始加人者的位置更新公式中, 直接让非饥饿的 个体一开始从发现者最优位置附近进行更新, 这样会导致 种群的多样性单一, 增加种群陷人局部最优的可能性。因 此, 这里引人正态变异算子对式 (2) 中的最优位置进行扰 动, 让非饥俄的加人者向发现者最优位置的变异解学习, 这 样能够增大种群多样性与跳出局部最优的能力。其中, 正 态变异公式为: ${\mathbf{X}}^t={\mathbf{X}}^t+\alpha \cdot {\mathbf{X}}^t$ 。为了避免仅加值的方法

影响算法性能, 在扰动公式中引入方向因子 $F$, 改进公式如 式 (4) (5) 所示。
$$\begin{array}{rl}& F=\{\begin{array}{c}-1,r<0.5\\ 1,\text{ 其他 }\end{array}(4)\\ & {\mathbf{X}}_{Rb\text{ estj }}^t={\mathbf{X}}_{\text{bestj }}^t+F\cdot \alpha \cdot {\mathbf{X}}_{\text{bextj }}^t(5)\end{array}$$
式 (4) (5) 中: $r$ 是取值范围在 $[0,1]$ 的随机数, $\alpha$ 是服从 $N(0,1)$ 的随机数。加人者更新公式改进如式 (6) 所示。
$${\mathbf{X}}_{i,j}^{t+1}=\{\begin{array}{ll}Q\cdot \exp \left(\frac{{\mathbf{X}}_{\text{uosstj }}^t-{\mathbf{X}}_{i,j}^t}{i^2}\right),& i>\frac{n}{2}\\ {\mathbf{X}}_{\text{Rbeetj }}^{t+1}+\left|{\mathbf{X}}_{i,j}^t-{\mathbf{X}}_{Rbeexj}^{t+1}\right|\cdot {\mathbf{A}}^{+}\cdot \mathbf{L},& \text{ 其他 }\end{array}\text{\hspace{1em}(6)}$$
式 (6)中: ${\mathbf{X}}_{R\text{ Recesj }}^t$ 是当前最优发现者的正态变异扰动解。

2.2 对立学习

对立学习是一种常用的跳出局部最优解位置的策略。 在原始麻雀搜索算法的侦查时, 最优位置的麻雀往最差解 靠拢,其他位置麻﨎往最优值靠拢。虽然往最差解位置搜 索, 一定程度上能够避免陷人局部最优, 但这样并不利于种 群的收敛。而对立学习不仅能帮助个体快速逃离当前位 置, 而且对立位置相比于当前最差位置, 其适应度值更有可 能比于当前位置更优, 因此,在侦查部分的位置更新公式引 人对立学习策略, 其改进公式如式 (7):
$${\mathbf{X}}_{i,j}^{t+1}=\{\begin{array}{l}{\mathbf{X}}_{bestj}^t+\beta \cdot \left|{\mathbf{X}}_{i,j}^t-{\mathbf{X}}_{bestj}^t\right|,{\mathbf{f}}_i>{\mathbf{f}}_{\mathrm{g}}\\ lb+ub-\beta \cdot {\mathbf{X}}_{i,j}^t,\text{ 其他 }\end{array}\text{\hspace{1em}(7)}$$
式 (7) 中: $\beta$ 是服从 $N(0,1)$ 的随机数, $lb$ 与 $ub$ 分别为搜索 空间的下界和上界。

2.3 正交对立学习

正交对立学习策略是利用当前解与对立解, 通过正交 实验设计, 以较少的实验次数找到不同因素的水平最佳组 合的一种方法。目前相关研究方面, 閤大海等 ${}^{[14]}$ 提出了基 于正交设计的反向学习策略, 并应用在差分进化算法上, 提 高了算法的鲁棒性; 周凌云等 ${}^{[15]}$ 基于萤火虫算法, 引人了 正交重心反向学习策略, 增强了算法求解复杂问题的能力; 基于此, 本文融合对立学习与正交学习, 提出正交对立学习 策略, 对麻雀搜索算法进行改进。该策略的基本思想是: 利 用当前位置与其对立位置, 根据正交表构建正交候选解, 接 着对各候选解进行评估, 最终取出其中最佳的正交组合。 通过这种方式, 充分利用个体和对立个体中各维度的信息 并找到最佳组合, 其流程如图 1
$${\mathbf{L}}_4\left(2^3\right)=\left[\begin{array}{lll}1& 1& 1\\ 1& 2& 2\\ 2& 1& 2\\ 2& 2& 1\end{array}\right]\text{\hspace{1em}(8)}$$
在正交表中,同一列的 1 和 2 分别代表第一个水平和第 二个水平的在该列的维度信息。矩阵中的第一行是当前个体 本身, 其他行是两个水平不同维度之间的正交组合, 式 (8)中只 需要进行 4 次评估, 即可找到当前解与对立解的最佳正交组 合。而针对本文的正交对立学习策略, 则需要构建 $D$ 因素二 水平的正交表, 其中 $D$ 为种群维度。随着维数的增多, 试验评 估的次数也会增加,但算法的收敛性能也会更好。

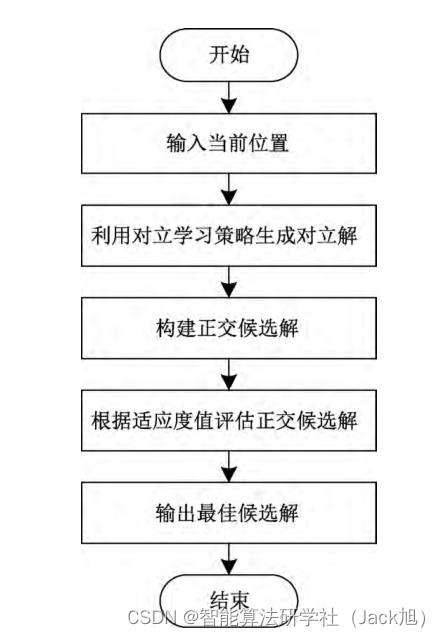
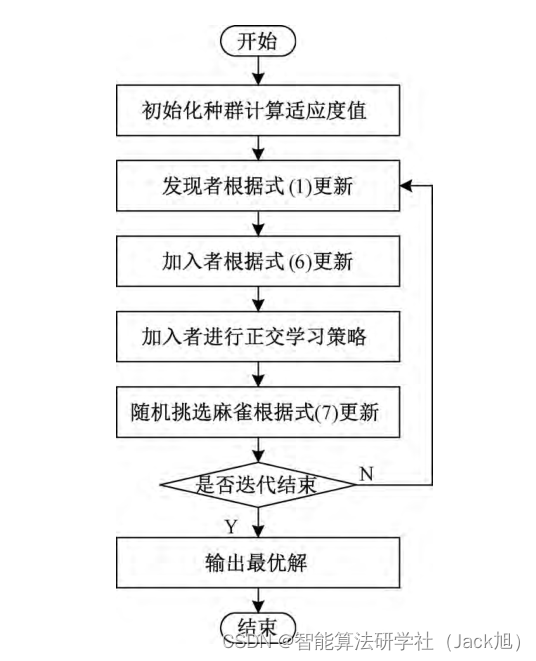
由于正交表包括个体本身位置, 每一个候选解均有相 同的概率成为最佳正交解, 存在经过 $M$ 次的评估后, 仍然 存在输出最优解为个体本身的可能性。假设种群中每一个 个体都进行正交学习, 这样固然能够更好的加快算法收敛 速度, 但这样同时也会大大增加实验评估的次数, 并不适用 于解决实际问题。因此, 本文正交对立学习策略仅应用在 加人者位置更新部分。在加人者按照式 (6) 更新后, 再利用 式 (7) 中的对立公式得到其对立解, 将以上两个位置按照 $D$ 因素二水平的正交表构建正交候选解, 经过计算适应度值 评估后, 将最佳正交解候选解作为当前加人者的最终更新 位置。通过这种方法, 能够提高算法收敛速度与精度的同 时避免算法陷人局部最优的问题。

3.实验结果

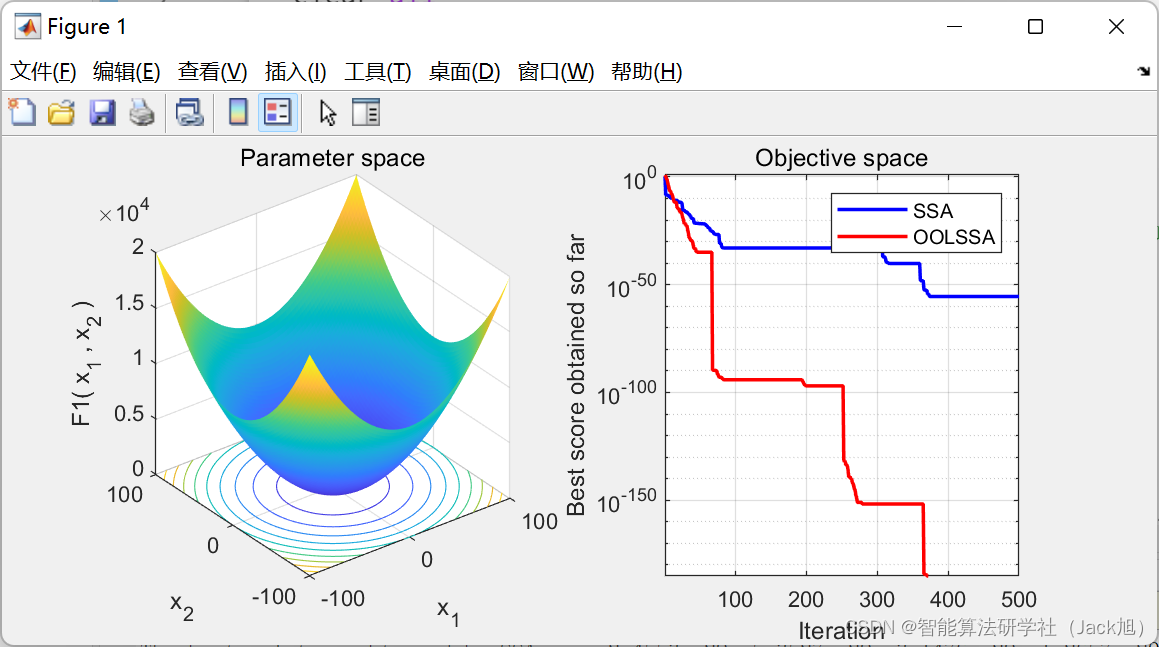
4.参考文献

[1]王天雷,张绮媚,李俊辉,周京,刘人菊,谭南林.基于正交对立学习的改进麻雀搜索算法[J].电子测量技术,2022,45(10):57-66.DOI:10.19651/j.cnki.emt.2209151.

5.Matlab代码

6.Python代码