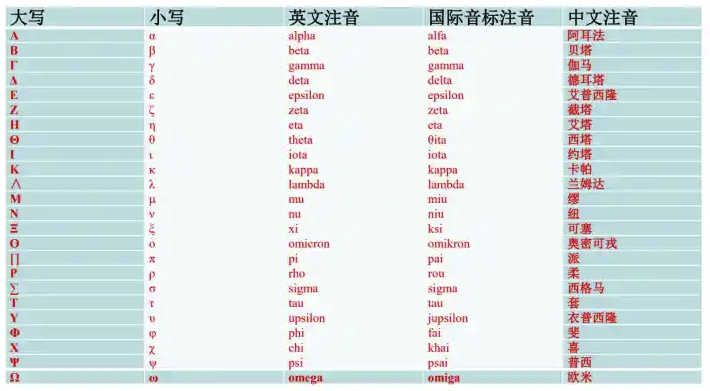
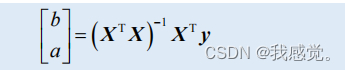先来一组对应关系:

一、使用 拟合。
拟合。
1.1代数计算
拟合后误差为,要找到一个a,使得
的和最小,计算
,用 f(a) 表示:
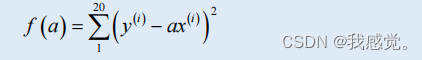
带入数据即可得到

易得f(a)最小时的a值。
1.2解超定方程组
用向量表示x和y:
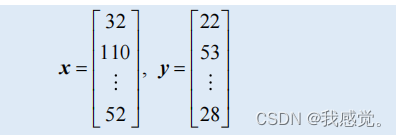
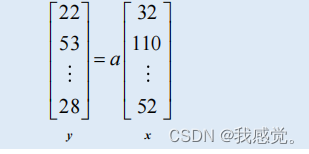
则解得:
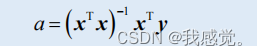
1.3几何意义
a为常数,故向量 与向量 x 维数相同且共线。既然找到了一个最合适得a,那么就一定有误差向量
与向量
垂直,即
,解得:
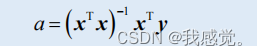
二、使用  拟合
拟合
2.1代数计算
拟合后误差为,要找到一个a,b,使得
的和最小,计算
,表示为:
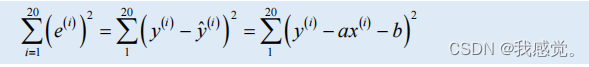
带入数据即可得到
![]()
求偏导易得f(a,b)最小时的a,b值。
2.2 解超定方程组
用向量表示x和y:

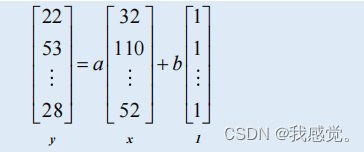
则可得:
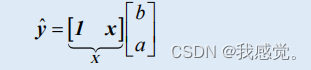
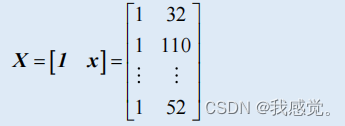
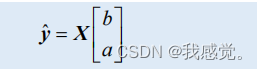
解超定方程组得
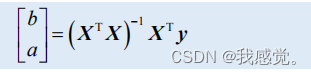
2.3几何意义
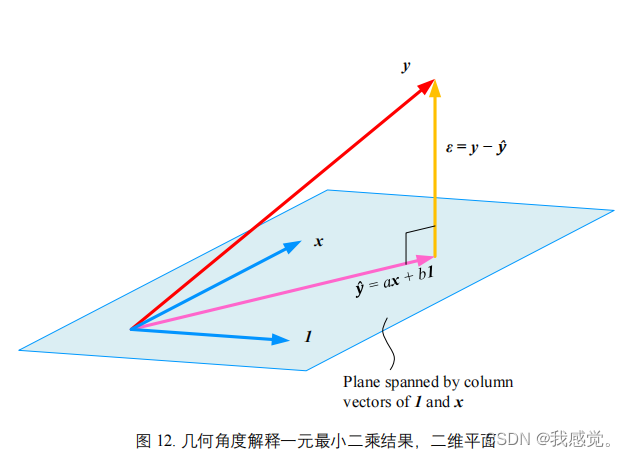
要想有最合适的a和b,就一定有误差向量 模值最小,则一定会有
在[1]向量和x向量的平面上的投影为
,即:

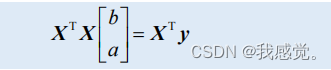
则可解得: