文章目录
- 1.1连续信号与离散信号
- 1.1.2信号能量与功率
- 能量
- 讨论无穷区间内功率和能量:
- 无限区间内的平均功率:
- 利用上述定义区分三种重要信号
- 1.2自变量的变换
- 1.2.1举例基本变换
- 1.2.2周期信号
- 1.2.3偶信号与奇信号
- 1.3指数信号与正弦信号
- 1.3.1连续时间复指数信号与正弦信号
- 1.3.2离散时间复指数信号与正弦信号
- 1.3.3离散时间复指数序列得周期性质
- 1.4单位冲激与单位阶跃函数
- 1.4.1单位脉冲和单位阶跃序列
- 1.4.2连续时间单位阶跃和冲激函数
- 1.5连续时间和离散时间系统
- 1.5.2 系统的互联
- 1.6基本系统性质
- 1.6.1
- 1.6.2 可逆性与可逆系统
- 1.6.3 因果性
- 1.6.4 稳定性
- 1.6.5 时不变性
- 1.6.6 线性
1.1连续信号与离散信号
信号:表示为一个或多个变量得函数
自变量:时间等
因变量:温度、波长、频率
区分:
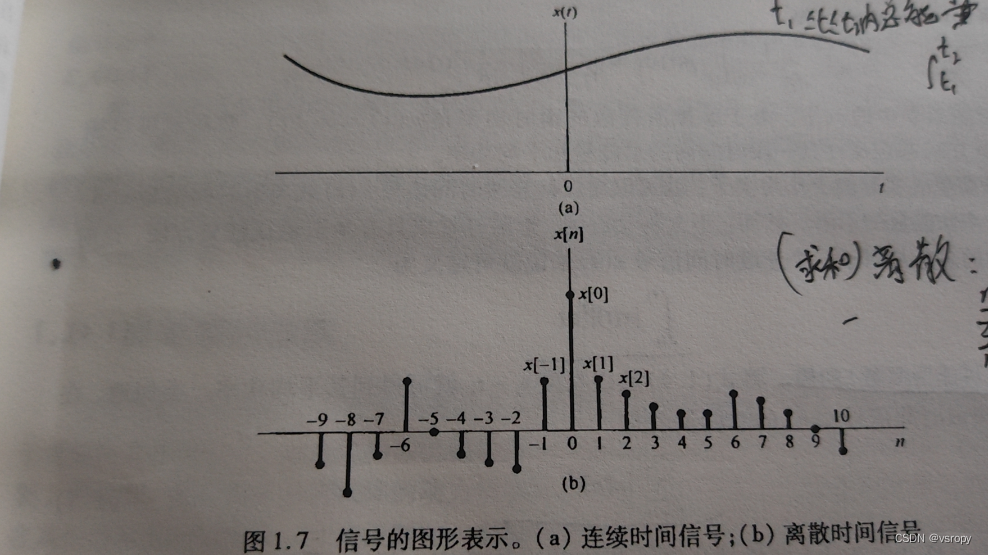
t :表示连续时间变量,用x(t)表示
n : 表示离散时间变量,用x[n]表示,仅仅在整数值上有定义。
1.1.2信号能量与功率
平均功率:1/ ( t 2 − t 1 ) (t_2-t_1) (t2−t1) ∫ t 1 t 2 p ( t ) d t \int^{t_2}_{t_1}p(t)dt ∫t1t2p(t)dt
能量
在
t
1
t_1
t1<=t<=
t
2
t_2
t2内总能量对于连续时间信号:
∫
t
1
t
2
∣
x
(
t
)
2
∣
d
t
\int^{t_2}_{t_1}|x(t)^2|dt
∫t1t2∣x(t)2∣dt,其中|x|记为x的模,除以
t
2
−
t
1
t_2-t_1
t2−t1得到平均功率。
在
n
1
<
=
n
<
=
n
2
n_1<=n<=n_2
n1<=n<=n2内离散时间信号x[n]的总能量为:
∑
n
=
n
1
n
2
∣
x
[
n
]
∣
2
\sum_{n=n_1}^{n_2}|x[n]|^2
n=n1∑n2∣x[n]∣2,除以区间内点数
n
2
−
n
1
+
1
n_2-n_1+1
n2−n1+1得到该区间的平均功率。
讨论无穷区间内功率和能量:
连续情况:
E
∞
E_\infty
E∞=
lim
T
→
∞
∫
−
T
T
∣
x
(
t
)
∣
2
d
t
\lim_{T \to \infty}\int^{T}_{-T}|x(t)|^2dt
limT→∞∫−TT∣x(t)∣2dt =
∫
−
∞
∞
∣
x
(
t
)
∣
2
d
t
\int^{\infty}_{-\infty}|x(t)|^2dt
∫−∞∞∣x(t)∣2dt
离散情况:
E
∞
=
lim
N
→
∞
∑
n
=
−
N
+
N
∣
x
[
n
]
∣
2
=
∑
n
=
−
∞
+
∞
∣
x
[
n
]
∣
2
E_\infty=\lim_{N\to \infty}\sum_{n=-N}^{+N}|x[n]|^2=\sum_{n=-\infty}^{+\infty}|x[n]|^2
E∞=N→∞limn=−N∑+N∣x[n]∣2=n=−∞∑+∞∣x[n]∣2
无限区间内的平均功率:
连续情况:
p
∞
=
lim
T
→
∞
1
2
T
∫
−
T
T
∣
x
(
t
)
∣
2
d
t
p_\infty=\lim_{T \to \infty}\frac{1}{2T}\int^{T}_{-T}|x(t)|^2dt
p∞=limT→∞2T1∫−TT∣x(t)∣2dt
离散情况:
p
∞
=
lim
N
→
∞
1
2
N
+
1
∑
n
=
−
N
+
N
∣
x
[
n
]
∣
2
p_\infty=\lim_{N \to \infty}\frac{1}{2N+1}\sum_{n=-N}^{+N}|x[n]|^2
p∞=N→∞lim2N+11n=−N∑+N∣x[n]∣2
利用上述定义区分三种重要信号
p
∞
=
lim
T
→
∞
E
∞
2
T
p_\infty=\lim_{T \to \infty}\frac{E_\infty}{2T}
p∞=limT→∞2TE∞
一、信号具有有限总能量,
E
∞
<
∞
E_\infty<\infty
E∞<∞,平均功率
p
∞
p_\infty
p∞为0
二、平均功率
p
∞
p_\infty
p∞有限信号,如
p
∞
p_\infty
p∞>0,那么
E
∞
=
∞
E_\infty=\infty
E∞=∞,如x[n]=4,
p
∞
p_\infty
p∞=16
三、
p
∞
p_\infty
p∞和
E
∞
E_\infty
E∞都不是有限的,如x(t)=t
1.2自变量的变换
1.2.1举例基本变换
1、时移
左加右减
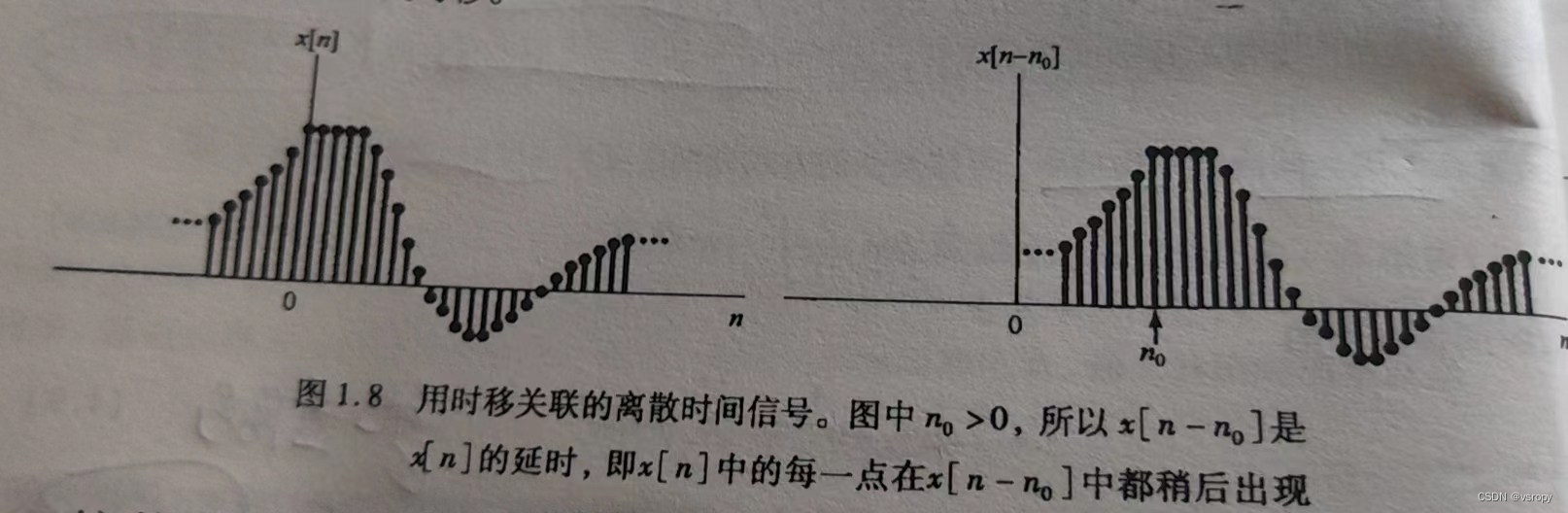
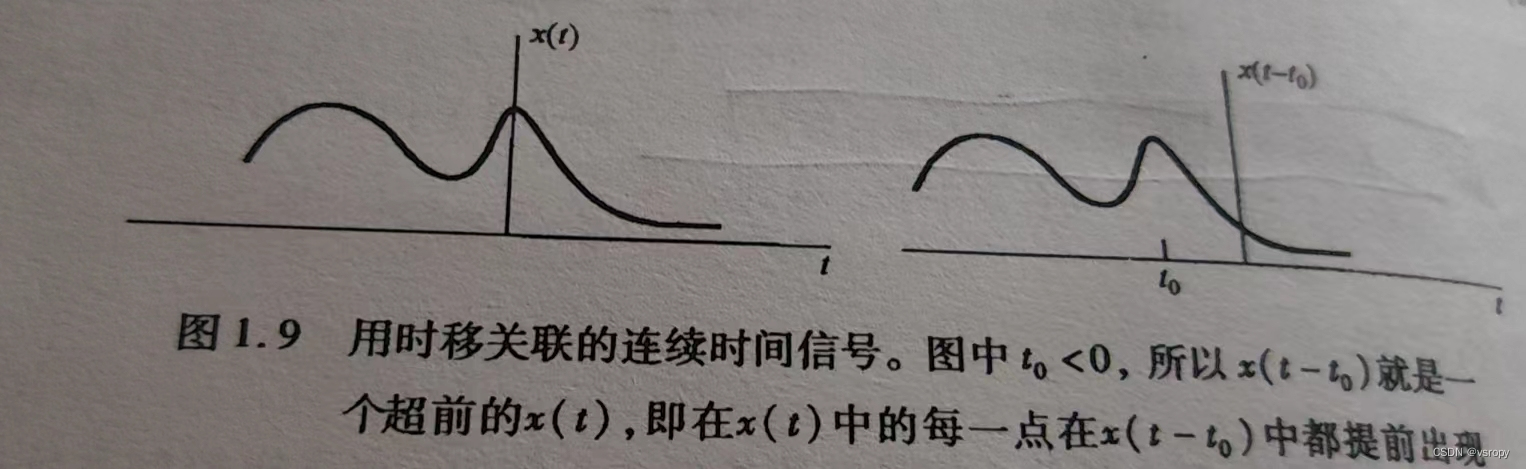
2、时间反转
以n=0和x=0为轴反转(即从末尾开始倒放)
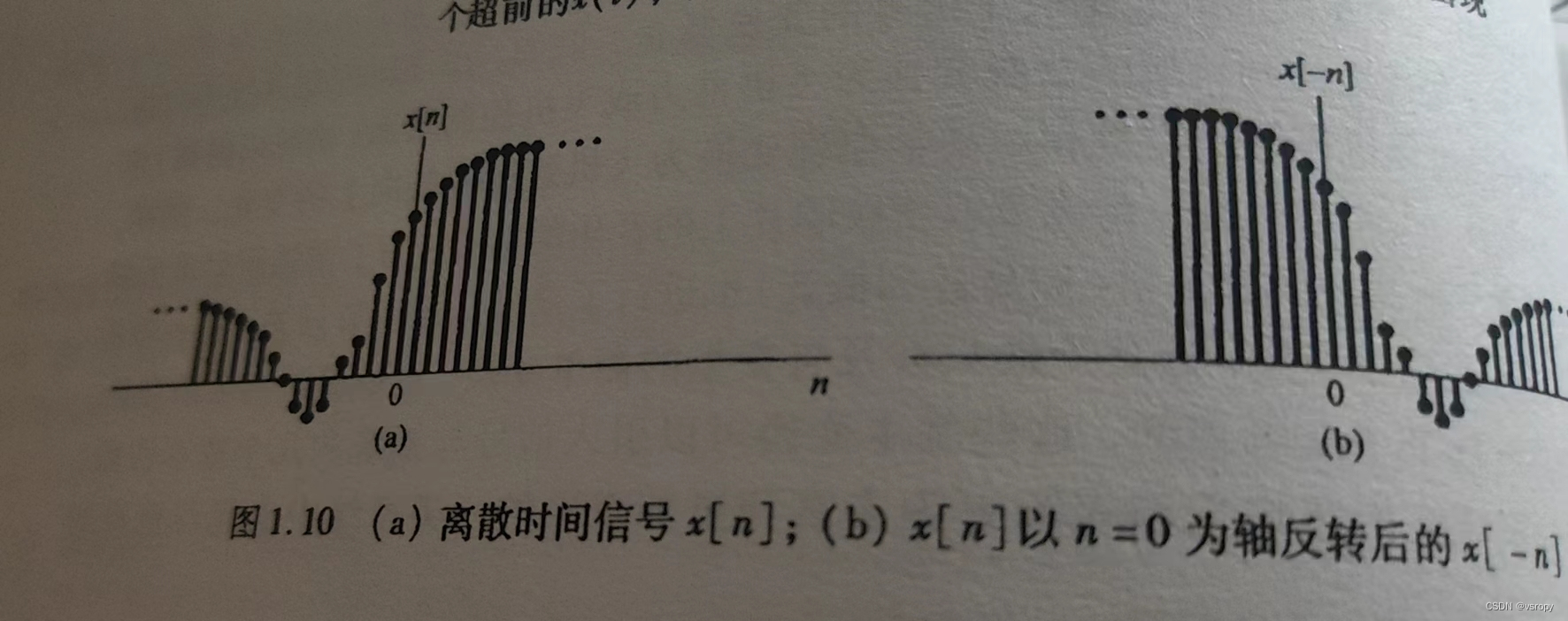
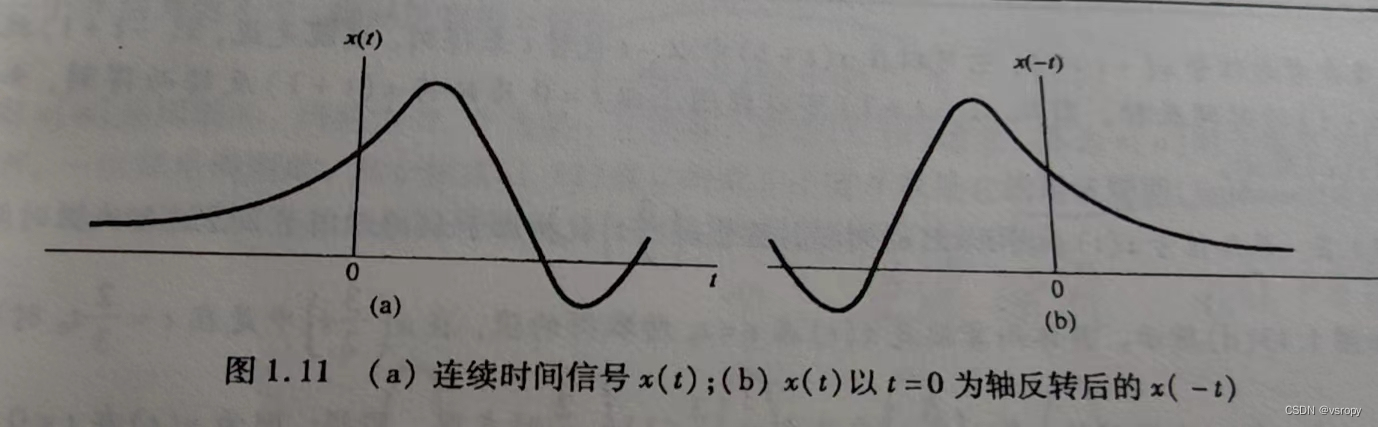
3、时间尺度变换
x(t)———>x(
α
\alpha
αt+
β
\beta
β)
x(t)—>x(at)
a
t
,
t^,
t,=t
t
,
t^,
t,=1/a *t
若
∣
α
∣
|\alpha|
∣α∣<1图像扩展,若
∣
α
∣
|\alpha|
∣α∣>1图像压缩,如t缩小成t/2,原本t=2的值,现在要t=4才行,图像延长了
1.2.2周期信号
当一个周期信号时移T后其值不变,这时就说x(t)是一个周期信号,周期为T
x(t)=x(t+T)
同理:x[n]=x[x+N] (1.12)
使式(1.12)成立的最小正值就是它的基波周期
1.2.3偶信号与奇信号
偶信号:
x(-t)=x(t)
x[-n]=x[n]
奇信号:
在t=0或n=0时必须为0
x(-t)=-x(t)
x[-n]=-x[n]
任何信号都能分解为两个信号之和,其中之一为偶信号,另一个为奇信号
1.3指数信号与正弦信号
1.3.1连续时间复指数信号与正弦信号
x(t)=C
e
a
t
e^{at}
eat
一、实指数信号
若C和a都是实数,x(t)为实指数信号
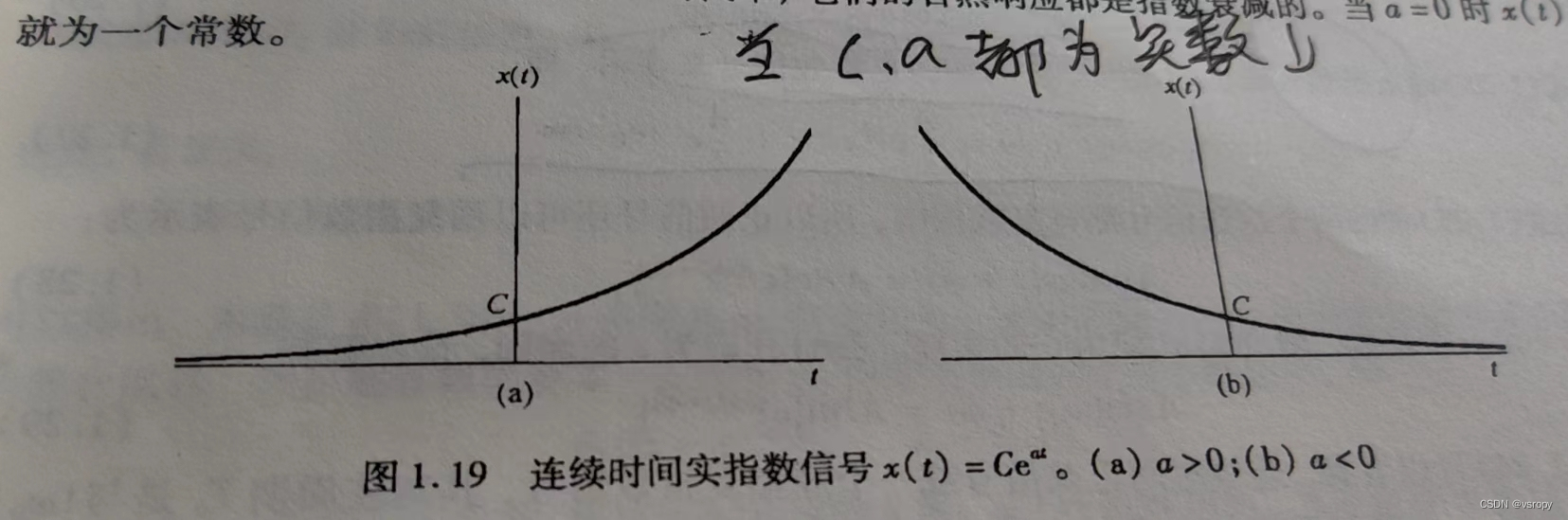
二、周期复指数
复指数信号将a限制为纯虚数:x(t)=
e
j
w
0
t
e^{jw_0t}
ejw0t
证明是周期信号:
e
j
w
0
(
t
+
T
)
=
e
j
w
0
t
e^{jw_0(t+T)}=e^{jw_0t}
ejw0(t+T)=ejw0t
由于
e
j
w
0
(
t
+
T
)
=
e
j
w
0
t
e
j
w
0
T
e^{jw_0(t+T)}=e^{jw_0t}e^{jw_0T}
ejw0(t+T)=ejw0tejw0T
所以
e
j
w
0
T
=
1
e^{jw_0T}=1
ejw0T=1
若
w
0
=
0
w_0=0
w0=0,则x(t)=1,这时对任何T值x(t)都是周期的,若
w
0
w_0
w0不等0,那么使
e
j
w
0
T
=
1
e^{jw_0T}=1
ejw0T=1成立的最小T值,即基波周期
T
0
T_0
T0应为
T
0
=
2
Π
∣
w
0
∣
T_0=\frac{2Π}{|w_0|}
T0=∣w0∣2Π
与周期复指数信号相关的信号——正弦信号:
x
(
t
)
=
A
c
o
s
(
w
0
t
+
ϕ
)
x(t)=Acos(w_0t+\phi)
x(t)=Acos(w0t+ϕ)
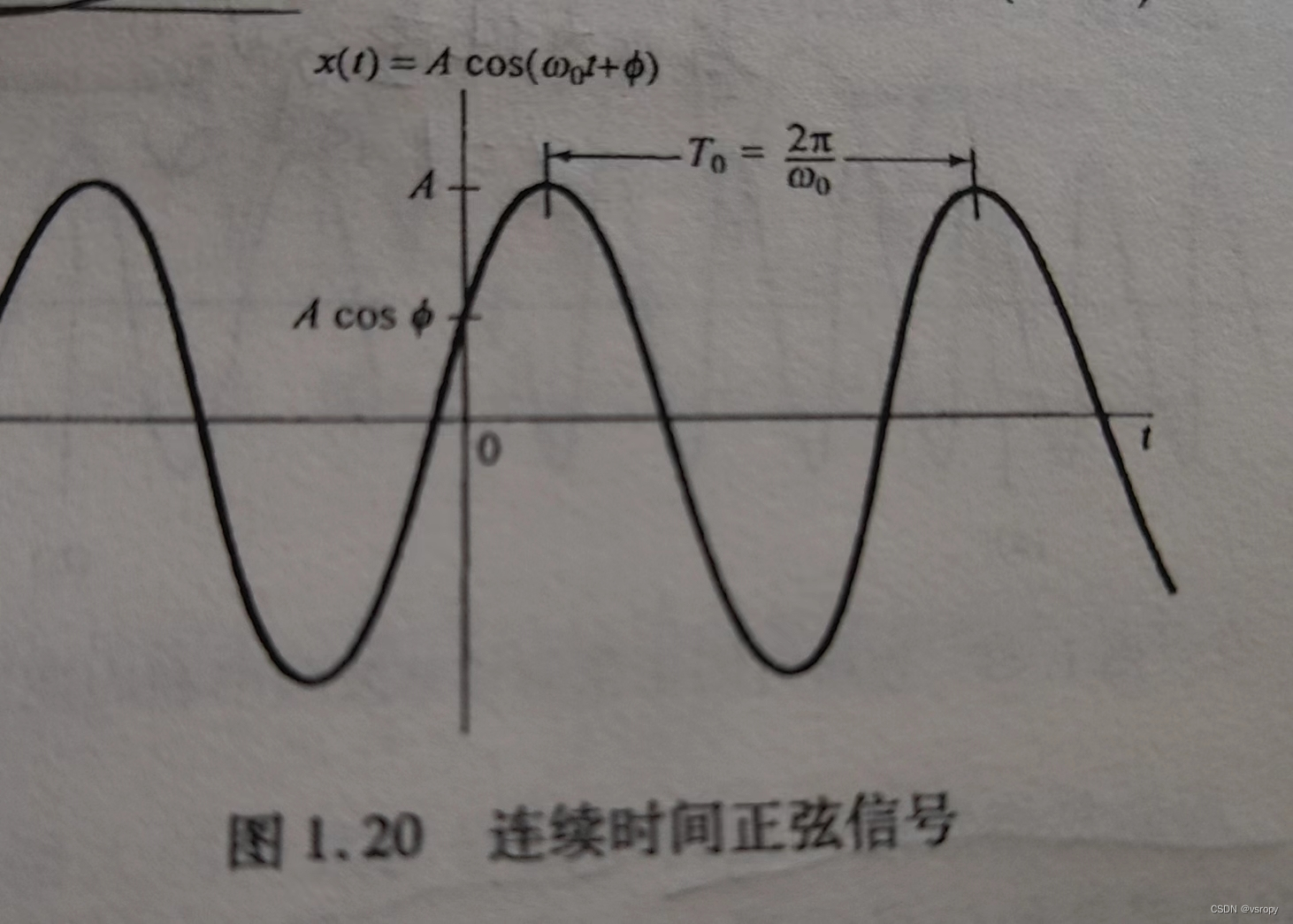
其基波周期也是
T
0
=
2
Π
∣
w
0
∣
T_0=\frac{2Π}{|w_0|}
T0=∣w0∣2Π
w
0
减小,
x
(
t
)
振荡速率减慢
w_0减小,x(t)振荡速率减慢
w0减小,x(t)振荡速率减慢
利用欧拉关系复指数信号可以用与其相同的基波周期的正弦信号来表示:
复指数——>正弦
e
j
w
0
t
=
c
o
s
w
0
t
+
j
s
i
n
w
0
t
e^{jw_0t}=cosw_0t+jsinw_0t
ejw0t=cosw0t+jsinw0t
正弦——>复指数
A
c
o
s
(
w
0
t
+
ϕ
)
=
A
2
e
j
ϕ
e
j
w
0
t
+
A
2
e
−
j
ϕ
e
−
j
w
0
t
Acos(w_0t+\phi)=\frac{A}{2}e^{j\phi}e^{jw_0t}+\frac{A}{2}e^{-j\phi}e^{-jw_0t}
Acos(w0t+ϕ)=2Aejϕejw0t+2Ae−jϕe−jw0t
周期复指数信号是重要的信号基本构造单元
对于一个复指数信号
e
j
w
t
e^{jwt}
ejwt,要成为周期信号的必要条件
e
j
w
0
t
0
=
1
e^{jw_0t_0}=1
ejw0t0=1,那么
w
T
0
是
2
Π
的倍数,即:
w
T
0
=
2
Π
k
,
w
0
=
2
Π
T
0
wT_0是2Π的倍数,即: wT_0=2Πk,w_0=\frac{2Π}{T_0}
wT0是2Π的倍数,即:wT0=2Πk,w0=T02Π
一个成谐波关系的复指数信号的集合就是一组其基波频率是某一正频率
w
0
w_0
w0的整数倍的周期复指数信号,即
ϕ
k
(
t
)
=
e
j
w
0
t
,
k
=
0
,
1
,
2
,
3...
基波频率
∣
k
∣
w
0
\phi_k(t)=e^{jw_0t},k=0,1,2,3... 基波频率|k|w_0
ϕk(t)=ejw0t,k=0,1,2,3...基波频率∣k∣w0
三、一般复指数信号
考虑某一复指数
C
e
a
t
Ce^{at}
Ceat
将C用极坐标,a用笛卡尔坐标表示:
C
=
∣
C
∣
e
j
θ
C=|C|e^{j\theta}
C=∣C∣ejθ
a
=
r
+
j
w
0
a=r+jw_0
a=r+jw0
C
e
a
t
=
∣
C
e
j
θ
∣
e
(
r
+
j
w
0
)
t
=
∣
C
∣
e
r
t
e
j
(
w
0
t
+
θ
)
Ce^{at}=|Ce^{j\theta}|e^{(r+jw_0)t}=|C|e^{rt}e^{j(w_0t+\theta)}
Ceat=∣Cejθ∣e(r+jw0)t=∣C∣ertej(w0t+θ)
利用欧拉公式:
C
e
a
t
=
∣
C
∣
e
r
t
c
o
s
(
w
0
t
+
θ
)
+
j
∣
C
∣
e
r
t
s
i
n
(
w
0
t
+
θ
)
Ce^{at}=|C|e^{rt}cos(w_0t+\theta)+j|C|e^{rt}sin(w_0t+\theta)
Ceat=∣C∣ertcos(w0t+θ)+j∣C∣ertsin(w0t+θ)
若r=0,实部和虚部都是正弦,若r>0,实部和虚部是一个呈指数增长的正弦信号,若r<0则衰减。
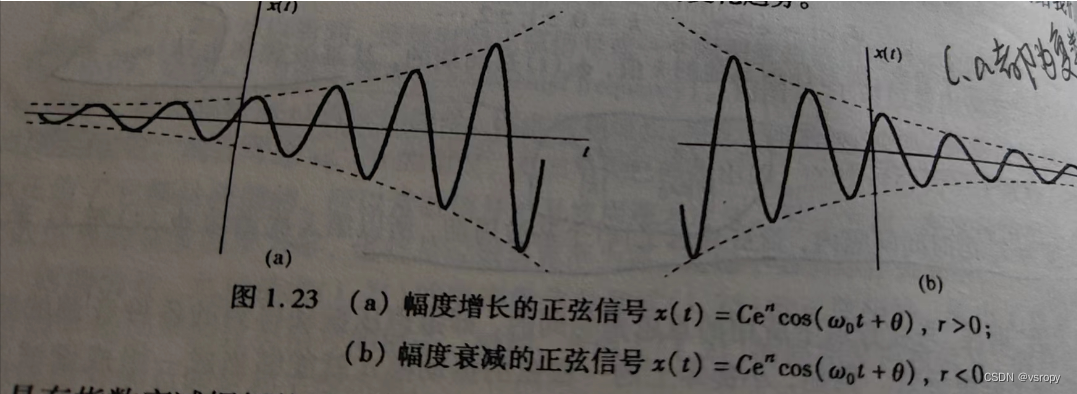
1.3.2离散时间复指数信号与正弦信号
x
[
n
]
=
C
α
n
x[n]=C\alpha^n
x[n]=Cαn
若令
α
=
e
β
,则有另一种表现形式
x
[
n
]
=
C
e
n
β
\alpha=e^\beta,则有另一种表现形式x[n]=Ce^{n\beta}
α=eβ,则有另一种表现形式x[n]=Cenβ
实指数信号
C和
α
都是实数
\alpha都是实数
α都是实数
正弦信号
若
β
局限为纯虚数,即
∣
α
∣
=
1
得:
x
[
n
]
=
e
j
w
0
n
,
同样可化为正弦
x
[
n
]
=
A
c
o
s
(
w
0
n
+
ϕ
)
若\beta局限为纯虚数,即|\alpha|=1得:x[n]=e^{jw_0n},同样可化为正弦x[n]=Acos(w_0n+\phi)
若β局限为纯虚数,即∣α∣=1得:x[n]=ejw0n,同样可化为正弦x[n]=Acos(w0n+ϕ)
上述两式子就是离散时间信号中具有无限能量和有限平均功率得例子,因为
∣
e
j
w
0
n
∣
=
1
|e^{jw_0n}|=1
∣ejw0n∣=1
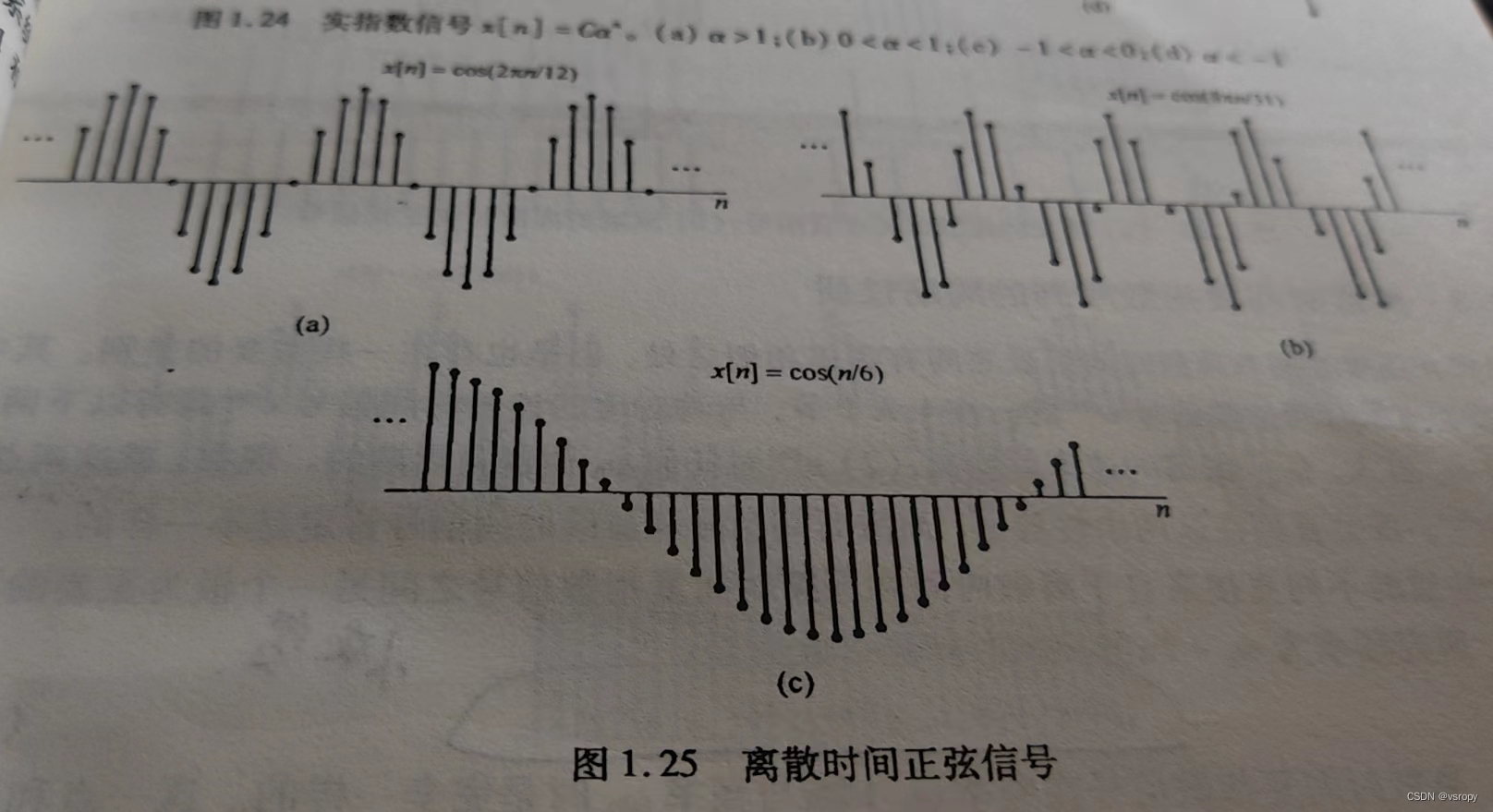
欧拉公式:
e
j
w
0
n
=
c
o
s
w
0
n
+
j
s
i
n
w
0
n
e^{jw_0n}=cosw_0n+jsinw_0n
ejw0n=cosw0n+jsinw0n
A
c
o
s
(
w
0
n
+
ϕ
)
=
A
2
e
j
ϕ
e
j
w
0
n
+
A
2
e
−
j
ϕ
e
−
j
w
0
n
Acos(w_0n+\phi)=\frac{A}{2}e^{j\phi}e^{jw_0n}+\frac{A}{2}e^{-j\phi}e^{-jw_0n}
Acos(w0n+ϕ)=2Aejϕejw0n+2Ae−jϕe−jw0n
一般复指数信号
以极坐标形式
C
=
∣
C
∣
e
j
θ
C=|C|e^{j\theta}
C=∣C∣ejθ
α
=
∣
α
∣
e
j
w
0
\alpha=|\alpha|e^{jw_0}
α=∣α∣ejw0
则有
C
α
=
∣
C
∣
∣
α
∣
n
c
o
s
(
w
0
n
+
θ
)
+
j
∣
C
∣
∣
α
∣
n
s
i
n
(
w
0
n
+
θ
)
则有C\alpha=|C||\alpha|^ncos(w_0n+\theta)+j|C||\alpha|^nsin(w_0n+\theta)
则有Cα=∣C∣∣α∣ncos(w0n+θ)+j∣C∣∣α∣nsin(w0n+θ)
对于
α
=
1
,
实部和虚部都是正弦,对
∣
α
∣
<
1
,
其实部和虚部为正弦序列乘以一个成衰减的序列,对
∣
α
∣
>
1
则增长
\alpha=1,实部和虚部都是正弦,对|\alpha|<1,其实部和虚部为正弦序列乘以一个成衰减的序列,对|\alpha|>1则增长
α=1,实部和虚部都是正弦,对∣α∣<1,其实部和虚部为正弦序列乘以一个成衰减的序列,对∣α∣>1则增长
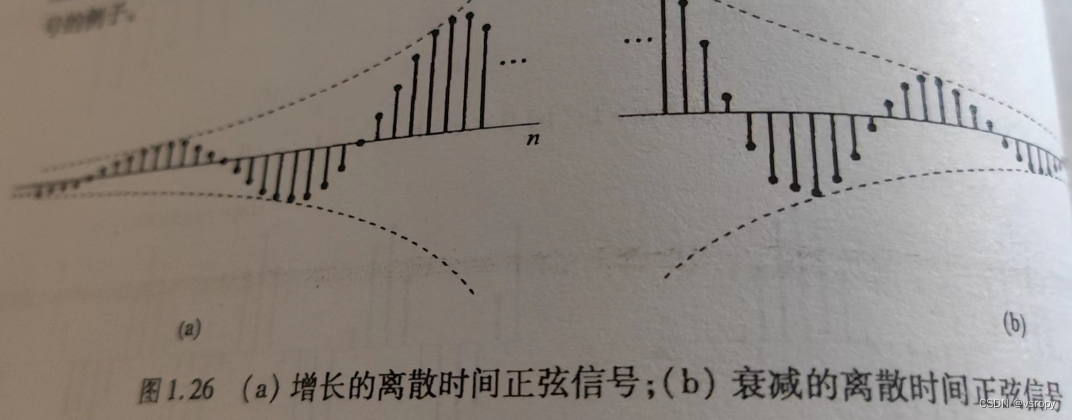
1.3.3离散时间复指数序列得周期性质
第一个性质
对于连续时间信号
e
j
w
0
n
,
w
0
越大,信号振荡频率越高
e^{jw_0n},w_0越大,信号振荡频率越高
ejw0n,w0越大,信号振荡频率越高
而离散时间信号没有这个性质
离散的性质是恢复
研究频率为
w
0
+
2
Π
的离散时间复指数信号:
e
j
(
w
0
+
2
Π
)
n
=
e
j
2
Π
n
e
j
w
0
n
=
e
j
w
0
n
研究频率为w_0+2Π的离散时间复指数信号: e^{j(w_0+2Π)n}=e^{j2Πn}e^{jw_0n}=e^{jw_0n}
研究频率为w0+2Π的离散时间复指数信号:ej(w0+2Π)n=ej2Πnejw0n=ejw0n
低频部分
w
)
位于
Π
偶数倍时,高频位于
Π
的奇数倍时,
e
j
Π
n
=
(
e
j
Π
)
n
=
(
−
1
)
n
低频部分w_)位于Π偶数倍时,高频位于Π的奇数倍时,e^{jΠn}=(e^{jΠ})^n=(-1)^n
低频部分w)位于Π偶数倍时,高频位于Π的奇数倍时,ejΠn=(ejΠ)n=(−1)n
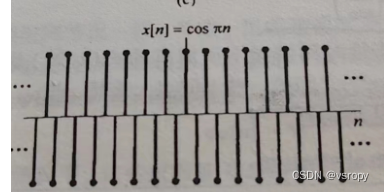
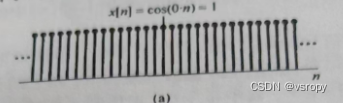
第二个性质——周期性
为了
e
j
w
0
n
周期为
N
>
0
,
那么必须
e
j
w
0
(
n
+
N
)
=
e
j
w
0
n
,
即要求
e
j
w
0
N
=
1
,
w
0
N
必须为
2
Π
的整数倍也就是说必须有一个整数
m
满足
,
w
0
N
=
2
Π
m
,
或者
w
0
2
Π
=
m
N
为了e^{jw_0n}周期为N>0,那么必须e^{jw_0(n+N)}=e^{jw_0n},即要求e^{jw_0N}=1,w_0N必须为2Π的整数倍也就是说必须有一个整数m满足,w_0N=2Πm,或者\frac{w_0}{2Π}=\frac{m}{N}
为了ejw0n周期为N>0,那么必须ejw0(n+N)=ejw0n,即要求ejw0N=1,w0N必须为2Π的整数倍也就是说必须有一个整数m满足,w0N=2Πm,或者2Πw0=Nm
若
w
0
/
2
Π
为有理数,
e
j
w
0
n
就是周期的,基波频率
2
Π
N
=
w
0
m
,
周期为
N
若w_0/2Π为有理数,e^{jw_0n}就是周期的,基波频率\frac{2Π}{N}=\frac{w_0}{m},周期为N
若w0/2Π为有理数,ejw0n就是周期的,基波频率N2Π=mw0,周期为N

1.4单位冲激与单位阶跃函数
1.4.1单位脉冲和单位阶跃序列
最简单的离散信号之一:单位脉冲或单位样本
δ
[
n
]
=
{
0
,
n
≠
0
1
,
n
=
0
\delta[n]=\left\{\begin{aligned}0,n≠0\\1,n=0\end{aligned}\right.
δ[n]={0,n=01,n=0
第二个基本离散信号:单位阶跃
u
[
n
]
=
{
0
,
n
<
0
1
,
n
>
0
u[n]=\left\{\begin{aligned}0,n<0\\1,n>0\end{aligned}\right.
u[n]={0,n<01,n>0

离散时间单位脉冲是离散时间单位阶跃的一次差分:
δ
[
n
]
=
u
[
n
]
−
u
[
n
−
1
]
\delta[n]=u[n]-u[n-1]
δ[n]=u[n]−u[n−1]
离散时间阶跃是单位样本的求和函数,即
u
[
n
]
=
∑
m
=
−
∞
n
δ
[
m
]
u[n]=\sum_{m=-\infty}^{n}\delta[m]
u[n]=m=−∞∑nδ[m]
当n<0时为0,在n>=0时为1,另外求和变量m改为k=n-m
u
[
n
]
=
∑
k
=
0
n
δ
[
n
−
k
]
u[n]=\sum_{k=0}^{n}\delta[n-k]
u[n]=k=0∑nδ[n−k]
单位脉冲序列的采样功能:
n=0时采样
x
[
n
]
δ
[
n
]
=
x
[
0
]
δ
[
n
]
x[n]\delta[n]=x[0]\delta[n]
x[n]δ[n]=x[0]δ[n]
n=
n
0
n_0
n0时采样
x
[
n
]
δ
[
n
−
n
0
]
=
x
[
n
0
]
δ
[
n
−
n
0
]
x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0]
x[n]δ[n−n0]=x[n0]δ[n−n0]
1.4.2连续时间单位阶跃和冲激函数
连续时间阶跃函数:
u
(
t
)
=
{
0
,
t
<
0
1
,
t
>
0
u(t)=\left\{\begin{aligned}0,t<0\\1,t>0\end{aligned}\right.
u(t)={0,t<01,t>0
在t=0是不连续的
连续时间单位阶跃是单位冲激的积分函数:
u
(
t
)
=
∫
−
∞
t
δ
(
r
)
d
r
u(t)=\int^t_{-\infty}\delta(r)dr
u(t)=∫−∞tδ(r)dr
反过来,单位冲激是单位阶跃的微分:
δ
(
t
)
=
d
u
(
t
)
d
t
\delta(t)=\frac{du(t)}{dt}
δ(t)=dtdu(t)
但在t=0处不连续,不可微,所以要考虑极限:
u(t)是当
△
—
>
0
时,
u
△
(
t
)
的极限
\triangle—>0时,u_{\triangle(t)}的极限
△—>0时,u△(t)的极限
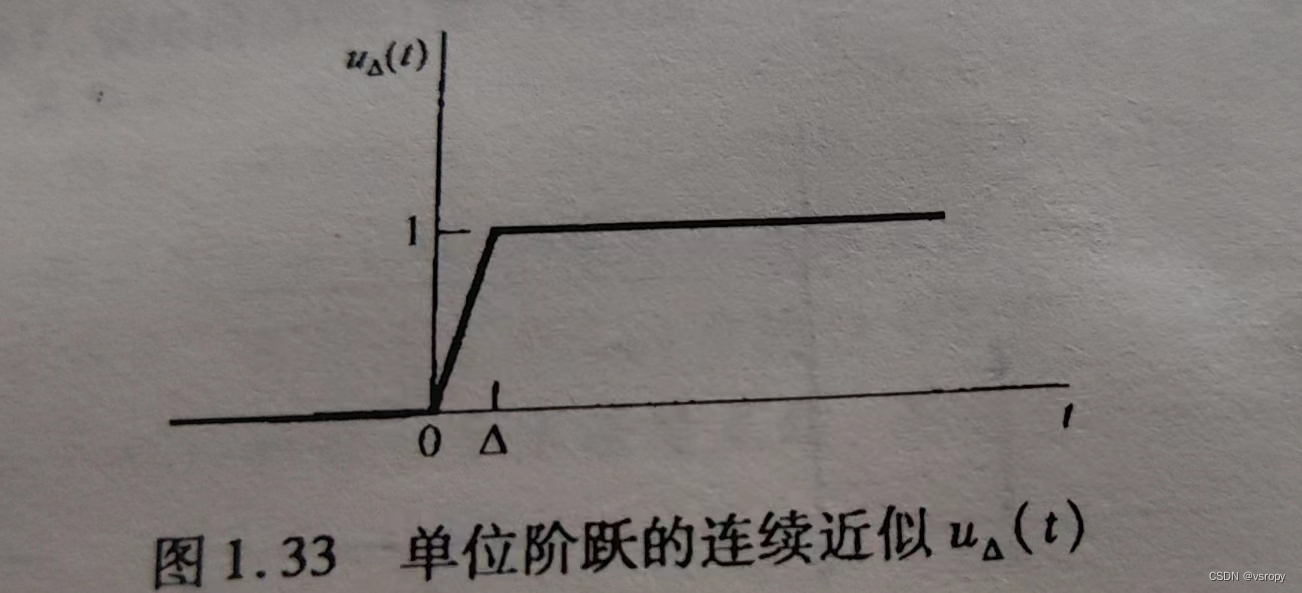
δ
△
(
t
)
面积始终保持单位面积,其极限形式
\delta_\triangle(t)面积始终保持单位面积,其极限形式
δ△(t)面积始终保持单位面积,其极限形式
δ
(
t
)
=
lim
△
→
0
δ
△
(
t
)
\delta(t)=\lim_{\triangle \to 0}\delta_\triangle(t)
δ(t)=lim△→0δ△(t)
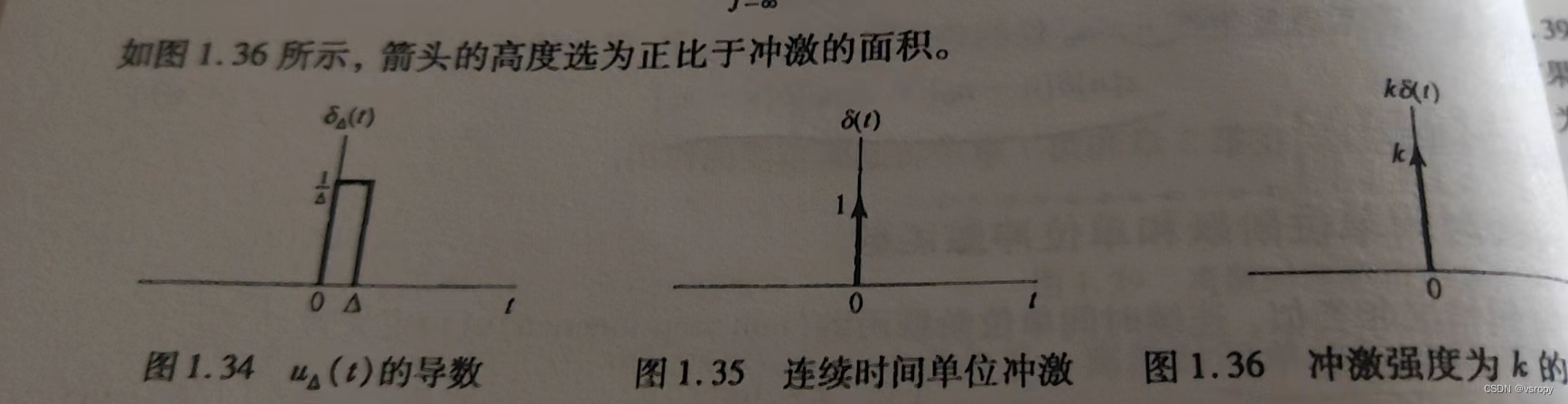
同样的采样函数:
x
(
t
)
δ
△
(
t
)
≈
x
(
0
)
δ
△
(
t
)
x(t)\delta_{\triangle(t)}≈x(0)\delta_{\triangle}(t)
x(t)δ△(t)≈x(0)δ△(t)
因为
δ
(
t
)
是
△
→
0
时
δ
△
(
t
)
的极限,所以
x
(
t
)
δ
(
t
)
=
x
(
0
)
δ
(
t
)
\delta(t)是\triangle \to 0时\delta_{\triangle(t)}的极限,所以 x(t)\delta(t)=x(0)\delta(t)
δ(t)是△→0时δ△(t)的极限,所以x(t)δ(t)=x(0)δ(t)
1.5连续时间和离散时间系统
x
(
t
)
→
y
(
t
)
x(t) \to y(t)
x(t)→y(t)
x
[
n
]
→
y
[
n
]
x[n] \to y[n]
x[n]→y[n]
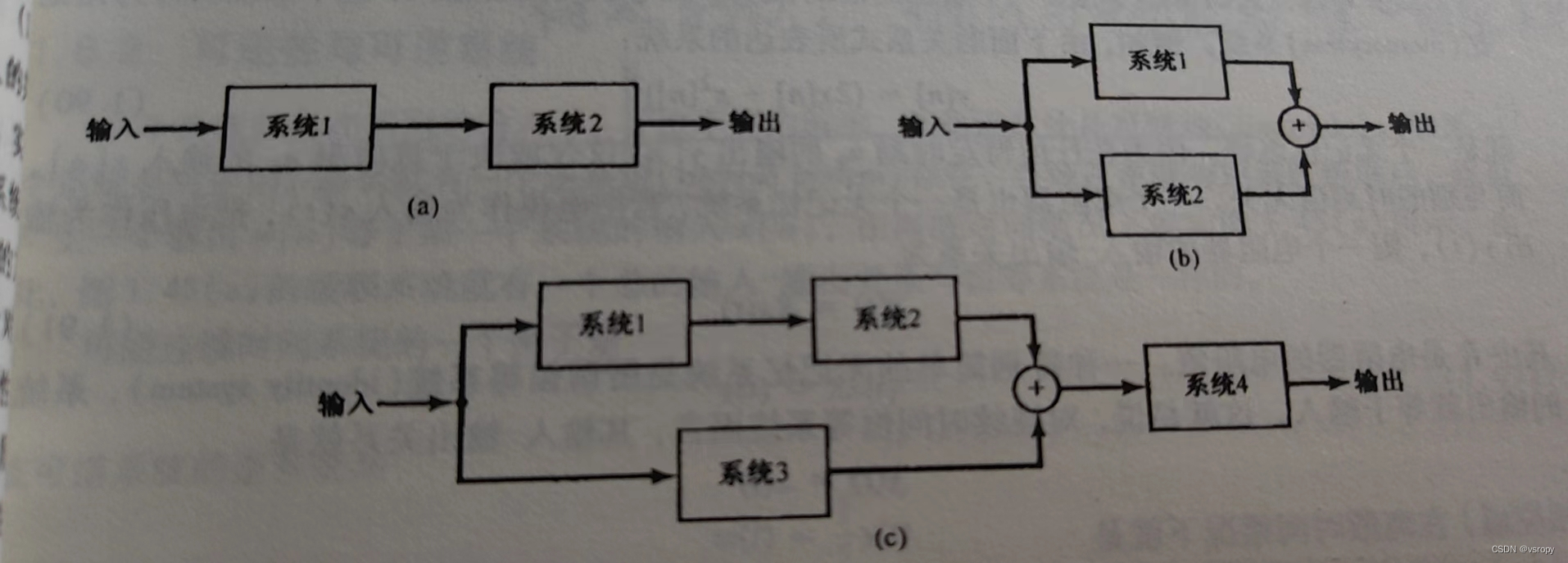
1.5.2 系统的互联
两个系统的串联或称级联,并联,反馈互联如下图
1.6基本系统性质
1.6.1
1.6.2 可逆性与可逆系统
一个系统在不同输入下,有不同的输出,这个系统就是可逆的
输出与输入无唯一对应关系,这个系统就是不可逆的
1.6.3 因果性
一个系统任意时刻的输出只取决于现在的输入及过去的输入
1.6.4 稳定性
一个稳定系统,若输入是有界的(即输入不是无界增长的),则系统的输出也必须有界,因此不可能发散
1.6.5 时不变性
若系统的特性和行为不随时间而变,该系统就是时不变的
当输入为
x
(
t
−
t
0
)
,
输出为
y
(
t
−
t
0
)
当输入为x(t-t_0),输出为y(t-t_0)
当输入为x(t−t0),输出为y(t−t0)
1.6.6 线性
y
1
(
t
)
+
y
2
(
t
)
是对
x
1
(
t
)
+
x
2
(
t
)
的响应
y_1(t)+y_2(t)是对x_1(t)+x_2(t)的响应
y1(t)+y2(t)是对x1(t)+x2(t)的响应
a
,
y
1
(
t
)
是对
a
x
1
(
t
)
的响应,
a
为常数
a^,y_1(t)是对ax_1(t)的响应,a为常数
a,y1(t)是对ax1(t)的响应,a为常数
第一个为可加性,第二个为比例性