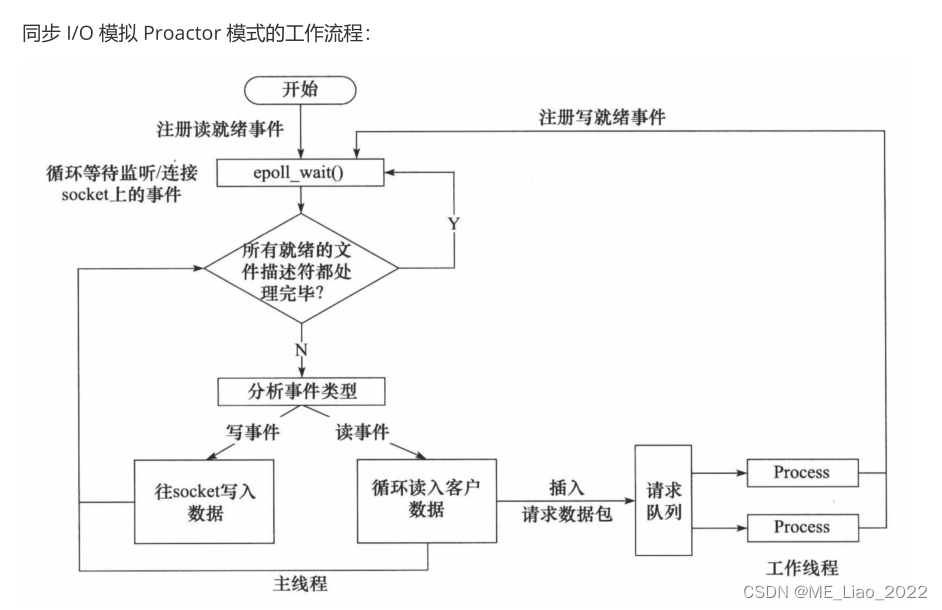
题目描述：
给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。

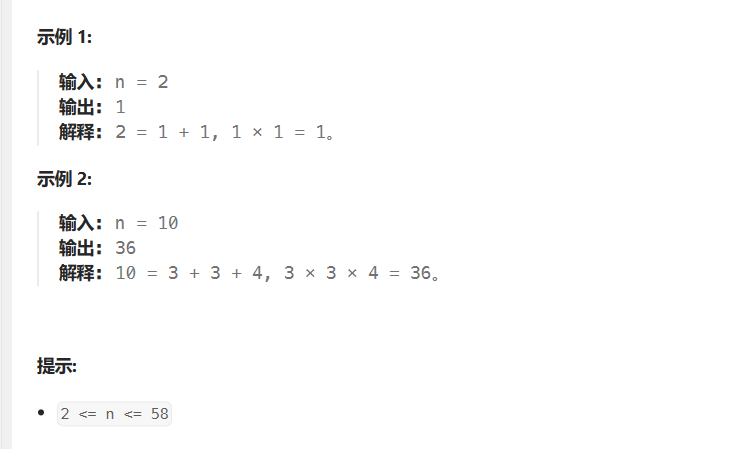
题目链接： LeetCode-343-整数拆分

解题思路：
还是根据动规五部曲，列出思路。

1. dp[i]：对 i 进行拆分，得到最大的乘积为dp[i]
2. 递归公式：j * dp[i-j]，j*(i-j)
3. 初始化：dp[2]=1 dp[1]=0 dp[0]=0（后面两个初始化其实也没有什么意义）
4. 遍历顺序：i=3开始遍历

代码实现：

class Solution {
    // 尽量拆成近似相等的数是得到的结果是最大的
    public int integerBreak(int n) {
        // 1. dp[i]：对 i 进行拆分，得到最大的乘积为dp[i]
        // 2. 递归公式：j * dp[i-j]
        // 3. 初始化：dp[2]=1 dp[1]=0 dp[0]=0
        // 4. 遍历顺序：i=3开始遍历

        int[] dp=new int[n+1];// 这里是 n+1，因为最后返回 n，否则会下标越界
        dp[0]=0;
        dp[1]=0;
        dp[2]=1;
        for (int i=3;i<=n;i++){
            // j<i/2;其实是进行了优化
            for (int j=1;j<=i/2;j++){
                // 放进来 dp[i]是因为每次都要比较 dp[i]的最大值
                dp[i]=Math.max(dp[i], Math.max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }
}