本文于 2007 年投稿于 ACM-SIGPLAN 会议¹。

概述

指针在代码编写过程中可能出现以下两种问题：

1. 存在一条执行路径，指针未成功释放（内存泄漏），如下面代码中注释部分所表明的：

   int foo()
   {
       int *p = malloc(4 * sizeof(int));
       if (p == NULL)
           return -1;
       int *q = malloc(4 * sizeof(int));
       if (q == NULL)
           return -1; // 注意这里，q为NULL时p一定不为NULL，但是函数直接返回，导致p所指向的区域未释放
       // some code to execute
       free(p);
       free(q);
       return 0;
   }
   

2. 存在一条执行路径，指针被重复释放（未定义行为），如 free 一个空指针。

   	int *p = (int *)malloc(4 * sizeof(int));
   	int *q = p;
   	free(q);
   	q = p;
   	free(q);
   

最笨拙的方法是枚举每一条可能的路径，依次判断。但是这显然是不切实际的。因而本文的主要工作是提出一个能够发现未释放指针或重复释放指针的高效算法，并进行了代码实现，提示编写者具体可能的错误原因。即给定一个程序，找到其中可能存在的这种问题。

首先进行控制流图（Condition-Flow Graph，CFG）的约定：

1. 赋值（运算节点）：$e=e^{\prime }$。
2. 函数调用：$e=f(p_1,p_2,\cdots ,p_m)$。
3. 返回：$\text{return}e$。
4. 分支节点：${\text{switch}}_e(c_1,n_1;c_2,n_2;\cdots ;c_k,n_k;n_t)$。即一个节点根据表达式 $e$ 的值不同可以有 $k+1$ 个分支跳转地址，分别记作 I n = { n 1 , n 2 , ⋯   , n k , n t } I_n=\{n_1,n_2,\cdots,n_k,n_t\} In​={n1​,n2​,⋯,nk​,nt​}，最后一个为默认跳转地址。

此外，本文将问题进行了规约：定义 $\mathrm{source}-\mathrm{sink}[n,m]$ 问题为从 $\mathrm{src}$ 会流入到 $[n,m]$ 个 $\mathrm{sink}$ 的条件可满足性问题。对于未释放，则是 $\mathrm{source}-\mathrm{sink}[0,0]$ 问题，而多次释放则是 $\mathrm{source}-\mathrm{sink}[2,\infty ]$ 问题，而合法性判断是 $\mathrm{source}-\mathrm{sink}[1,1]$ 问题。

算法流程

整体算法流程图如下所示：

1. 利用编译器前端搭建 CFG。
2. 到达定值点分析
3. 值流图构建
4. 无条件可达性分析，即不考虑具体控制流图上条件进行的分析
5. 条件可达性分析，即考虑控制流图上条件进行的分析。

在实现该算法的同时还需要调用：

1. 指针区域分析，即分析流图中每个指针所指向的内存区域。
2. 条件分析。
3. SAT（可满足性问题）解决器，即给定一组条件约束，返回一组可满足所有条件的初始值或报告无解。下文会将本论文中提出的问题规约到可满足性问题。

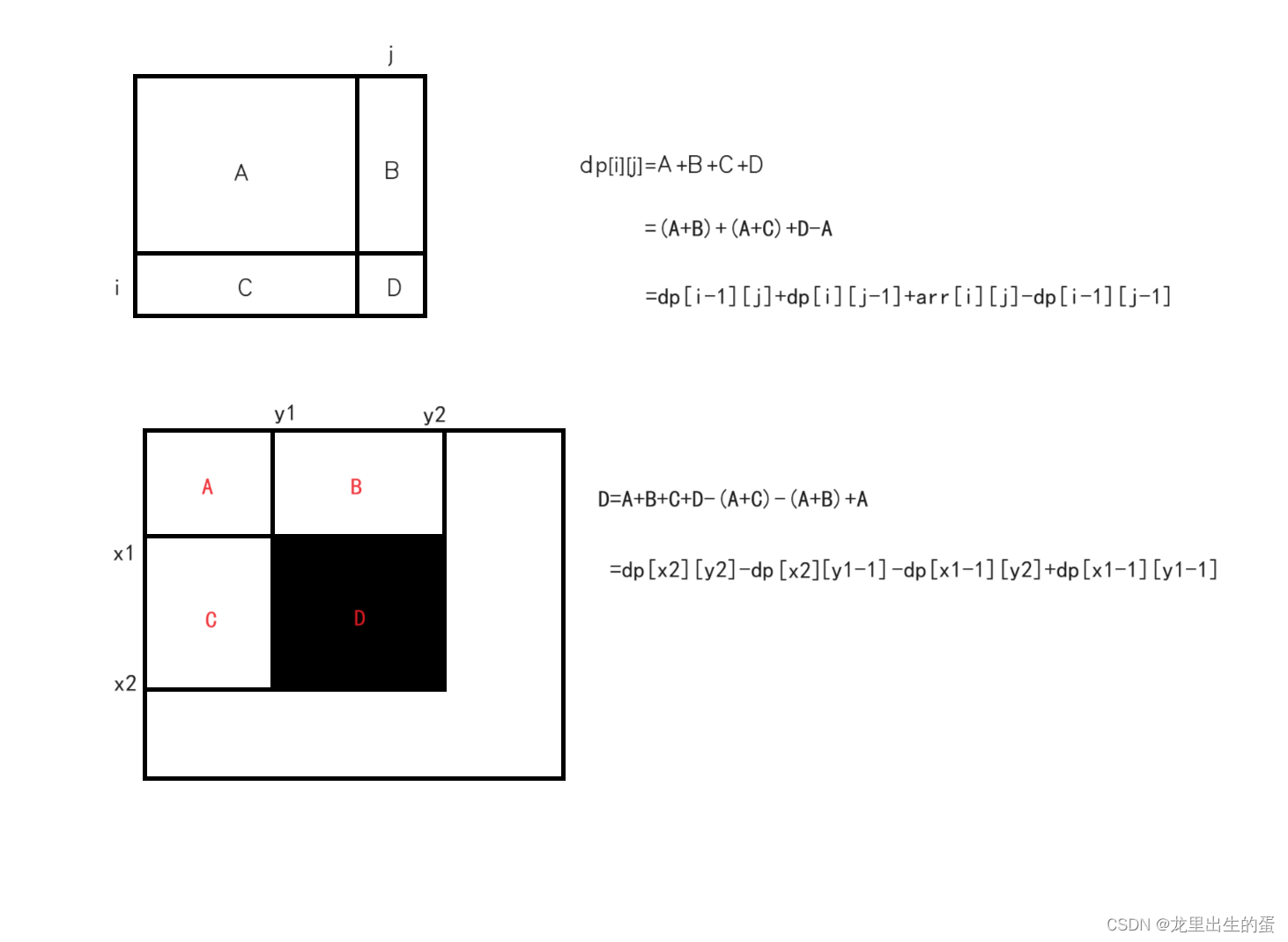
到达-定值分析（Reaching-Definition Analysis）

编译原理中经典的数据流分析方法。下文中用 $pdom(x,n,m)$ 来描述变量 $x$ 能不能从 CFG 上流图节点 $n$ 值不发生改变的到节点 $m$。论文中的 $S$ 仅为一个记忆化的集合，不做具体参数使用。$pdom$ 的计算使用逆向数据流分析方法：
$$pdom(x,n,m)=\{\begin{array}{l}true,m=n\\ false,\text{n 没有出边（返回节点）}\\ {\bigwedge }_{i\in I_n}pdom(x,i,m){\wedge }^{\neg }define(x,i),\text{其他情况}\end{array}$$
其中 $define(x,i)$ 表示 $i$ 节点没有进行对变量 $x$ 的赋值操作。

构建值流图（Value-Flow Graph）

在构建值流图之前首先需要介绍 free 函数的工作原理或特性：

1. 它释放传入参数给定的指针所指向的区域，也就是说它是针对内存区域而非指针的。例如下面的两个例子：

   1. 下面代码中 p1 和 p2 指针所指向的区域都被释放了。

   下面代码中 p 指针指向区域并未完全释放——p 指针所指向的区域仍有一个 int 大小的空间未释放。

   	int *p = malloc(4 * sizeof(int));
   	int *q = p + 1;
   	free(q);
   

基于以上两个特性，构建如下的节点：

1. 赋值（运算）节点。针对 CFG 上每个形如 $x=y$ 形式的赋值语句都对应一个 VFG 的节点。

2. 内存区域节点。由于 free 是针对区域而非指针型变量，因而需要用一个单独的节点描述它是否有被释放的途径。该部分节点用 $n_r$ 表示，可以使用这篇论文²中的方法快速描述代码中每个指针可能对应的内存区域集合。

   这里还需要注意的是，由于指针存在加减法操作，因而这里需要额外使用一个偏移量来去衡量该内存地址的具体使用情况。

3. 释放节点。每个 free 函数调用的节点都对应一个 VFG 上的汇（sink）点。

4. 函数调用实参节点。由于进行函数调用，可以视为进行一次变量的值使用，记为 $x_{@}n$。

5. 函数调用形参节点。在被调用函数（callee）中该函数作为新变量使用，同时它对应于调用函数（caller）的一个变量。为避免函数多次调用导致边关系混乱，因而新建一个形参节点以解决图过于混乱的问题，记为 $[p]$。

6. 函数返回节点。函数的返回值可能在 caller 中作为一个新变量继续存在，并涉及后续赋值和计算。

遍历 CFG，按如下规则建图（假设当前节点为 $n$）：

1. 赋值语句 $y=x$、释放节点 $free(x)$、返回节点 $return(x)$：将所有 $x$ 的定值点集合 $n_x$ 建立一条边连到 $n$ 节点。
2. $y=f(x_1,x_2,\cdots ,x_m)$：对于每个函数实参 $x_i$，首先将 $x_i$ 的定值点集合连接一条边到对应的实参节点（$n_{x_i}\to {x_i}_{@}n$），然后每个实参节点连接到形参节点 ${x_i}_{@}n\to p_i$，最后将 callee 函数的返回节点 $n_{\mathrm{ret}}^f$ 连接到当前函数调用节点（该语句可以视为一种特殊类型的赋值语句）$n_{\mathrm{ret}}^f\to n$。
3. 对于赋值变量中 $x$ 或 $y$ 不是一个有效节点的（如 malloc 函数返回的堆区域指针），调用内存区域查询函数返回对应的内存区域节点。

无条件可达性分析（Unguarded Reachability Detection）

该步骤中忽略了程序流图中的条件，即认为所有的边都是可走到的，在这种情况下先简单分析是否每个 malloc 函数都有至少一个 free 与之对应。

1. 枚举一个起始点 $src$，首先找到 VFG 顺向流图中可到达节点集合 $F_{src}$
2. 找到 $F_{src}$ 中所有的 free 语句对应节点，记为 $K$。
3. 分类讨论：
   1. 如果 $K$ 为空，则该 malloc 语句无对应 free 语句，直接报告内存泄漏。
   2. 如果从该 $src$ 节点可以到达一个内存区域节点，则说明该代码片段中存在全局变量，暂时不继续分析该代码的内存泄漏问题，直接退出。
   3. 找到能从 $src$ 到并且能到达 $K$ 的集合 $R$，并将 $R$ 集合传递到下一步继续分析。

条件可达性分析（Guarded Reachability Detection）

预处理

首先在 CFG 上进行条件分析。考虑每个分支节点 $n$ 需要满足其分支出口唯一，即对于分支节点 $n$：${\text{switch}}_e(c_1,n_1;c_2,n_2;c_k,n_k;n_t)$，需要满足：
$$C_n=\left[\underset{i}{\bigvee }(e=c_i{)}_n\right]\wedge \left[\underset{i\ne j}{\bigwedge }\overline{(e=c_i{)}_n\wedge (e=c_j{)}_n}\right]$$
即存在一条出路，且不存在一个条件同时满足两条出路。

定义函数 $cg(x,n,m)$（下简写成 $cguard(n\to m)$，其中程序点 $n$ 为形如 $x=e$ 的赋值语句）表示变量 $x$ 从程序点 $n$ 到 $m$ 需要满足的输入条件集合，有如下递推：
$$cg(x,n,m,E)=\{\begin{array}{l}true,\text{如果满足支配关系即 pdom(x,n,m)}\\ cg(x,n_1,m,E),\text{n 处无分支，n1 为 n 语句的唯一后续语句}\\ {\bigvee }_{i\in I_{n,x,E}}cond(n,n_i,E)\wedge cg(x,n_i,m,E\cup \{⟨n,n_i⟩\}),\text{其他情况}\end{array}$$
其中$I_{n,x,E}$ 表示满足后续节点不是形如 $define(n_i,x)$ 且 $⟨n,n_i⟩$ 不在 $E$ 中的后续节点集合 { n i } \{n_i\} {ni​}。$cond(n,n_i,E)$ 函数表示从 $n$ 节点走到 $n_i$ 节点所需要满足的条件，并且要求 $n$ 节点后续不能有 $E$ 中的边：
$$cond(n,n_i,E)=\{\begin{array}{l}(e=c_i{)}_n,\text{n 是一个分支节点，且 n 的后续集合不在 E 集合中}\\ true,\text{其他情况}\end{array}$$
这里 $(e=c_i{)}_n$ 表示在程序分支判断点 $n$ 处进行条件判断 $e=c_i$。

这里加入 $E$ 集合（已遍历的边集合）作为参数是方便代码实现上的，由于流图中可能有环存在，因而不能重复遍历同一条边，通过在状态中多维护一个 $E$ 集合可以有效防止重复遍历到同一条边。在 $cond$ 中，显然要进入循环然后退出该循环需要同时满足在循环的出口判断中 $e=c_i$ 和 $e\ne c_i$，这显然是永假的。因而这里加入了边的限制条件以防止上述情况的出现。当然这里会存在一个小漏洞就是仅判断了循环入口点的条件，未判断出口点的。这里会对未释放问题的判定产生一定的影响，但是对多重释放不会。

接下来就是考虑利用这些条件在 VFG 上进行条件判断。同样定义 $vguard(n,m)=vg(n,m)$ 函数表示从 VFG 图上 $n$ 节点走到 $m$ 的约束条件集合，有：
v g ( n , m , E ) = { t r u e , n = m ⋁ n → n ′ ∈ E c g u a r d ( n → n ′ ) ∪ v g ( n ′ , m , E ∪ { n → n ′ } ) , 其他情况 vg(n,m,E)= \begin{cases} true,n=m\\ \bigvee_{n \to n' \in E} cguard(n \to n') \cup vg(n',m,E \cup \{n \to n'\}),\texttt{其他情况} \end{cases} vg(n,m,E)={true,n=m⋁n→n′∈E​cguard(n→n′)∪vg(n′,m,E∪{n→n′}),其他情况​
和在 CFG 上的情况类似，这里只需要在 VFG 图上再加入 CFG 上的信息即可。

分析过程

考虑对于一个确定的 $src$ 节点和所有该指针的释放操作汇点 $K$，在 2.3 节中阐述的 $R$ 集合上进行分析。定义 $G_k=vguard(src,k)$，$C$ 为 $R$ 上所有的分支节点需要满足的 $C_n$ 的与集合。此时就满足了一个 SAT 问题的框架：

1. 如果此处存在一组初值指派满足 $\overline{{\vee }_{k\in K}{G}_k}\wedge C$，则表明存在某种初值指派，使得从该 $src$ 语句无法走到任何一个汇点，即发生了内存泄漏。
2. 如果存在一组初值指派，满足 $\exists i\ne j,G_i\wedge G_j\wedge C$，则表明某组初值指派可以到达两个不同的 free 语句，进行多次释放操作，因而发生未定义行为（Undefined Behavior）。

可以注意到上述的操作时间复杂度是比较高的，特别是对于有大量 malloc 语句存在的时候。因而本文中仅对操作数不超过阈值 $30$ 的代码进行分析。

本文同时实现了代码，将所有的错误种类分成以下几类：

1. 从未释放。又分为：a）指针作为局部变量在 main 函数或其他函数未释放；b）指针作为全局变量或存在于数组等结构中未释放。
2. 释放。又分为：a）一切条件下都能释放；b）某些情况下能释放，有些情况未释放。
3. 不能判定，认为释放了。这种情况通常因为分析语句过多导致超过阈值停止分析。

---

1. Cherem S, Princehouse L, Rugina R. Practical memory leak detection using guarded value-flow analysis[C]//Proceedings of the 28th ACM SIGPLAN Conference on Programming Language Design and Implementation. 2007: 480-491. ↩︎

2. Bjarne Steensgaard. Points-to analysis in almost linear time. In Proceedings of the ACM Symposium on the Principles of Programming Languages, St. Petersburg Beach, FL, January 1996. ↩︎