题目
113. 路径总和 II
中等
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
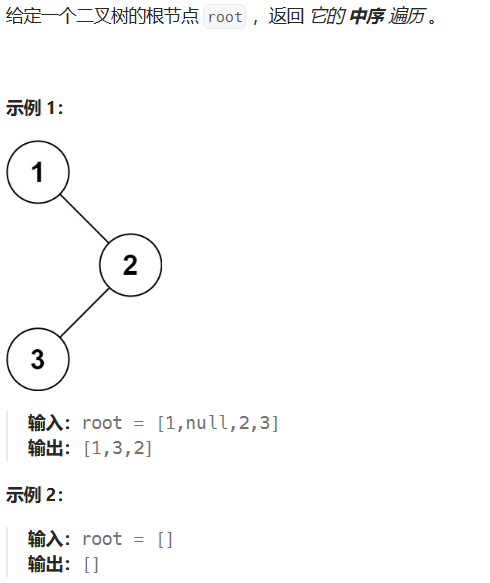
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
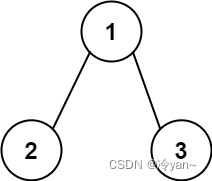
输入:root = [1,2,3], targetSum = 5 输出:[]
示例 3:
输入:root = [1,2], targetSum = 0 输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
思路和解题方法
首先判断当前节点
cur是否为叶子节点,并且路径和count是否等于 0。如果是,则将当前路径path加入到结果集ans中,并返回。如果当前节点不是叶子节点,继续判断其左右子节点是否存在。
如果左子节点存在,将左子节点的值加入到
path中,同时将路径和count减去左子节点的值,然后递归调用traversal函数。递归调用结束后,恢复路径和
count的值,即将左子节点的值从path中弹出,并将其加回到count中。如果右子节点存在,执行与左子节点类似的操作。
最后,将结果集
ans返回。在主函数
pathSum中,首先判断根节点是否为空。若为空,则直接返回空的结果集ans。如果根节点不为空,将根节点的值加入到
path中,并调用traversal函数开始遍历搜索满足条件的路径。最后,将结果集
ans返回。
复杂度
时间复杂度:
O(n*n)
时间复杂度为O(n * m),其中n是二叉树中节点的数量,m是满足路径和等于给定值的路径数量。
空间复杂度
O(n*m)
空间复杂度为O(n * m),需要使用一个二维vector来存储所有路径。
c++ 代码
class Solution { // 定义一个名为Solution的类
public: // 类作用域的开始
vector<vector<int>> ans; // 一个二维向量,用于存储所有满足条件的路径
vector<int> path; // 存储当前路径的节点值
// 定义一个名为traversal的私有方法,用于遍历二叉树并寻找满足条件的路径
void traversal(TreeNode *cur,int count)
{
// 如果当前节点是叶子节点,并且当前路径上的节点值总和等于目标值
if(!cur->left && !cur->right && count == 0)
{
// 将当前路径添加到结果中
ans.push_back(path);
return; // 结束此方法
}
// 如果当前节点不是叶子节点,直接返回
if(!cur->left&&!cur->right) return;
// 如果存在左子节点
if(cur->left)
{
// 将左子节点的值添加到当前路径中
path.push_back(cur->left->val);
// 减少目标值,因为左子节点的值会被加到子树的和中
count -= cur->left->val;
// 递归遍历左子树
traversal(cur->left,count);
// 恢复目标值,为后续节点做准备
count+=cur->left->val;
// 从当前路径中移除最后一个元素,为后续遍历做准备
path.pop_back();
}
// 如果存在右子节点
if(cur->right)
{
// 将右子节点的值添加到当前路径中
path.push_back(cur->right->val);
// 减少目标值,因为右子节点的值会被加到子树的和中
count -= cur->right->val;
// 递归遍历右子树
traversal(cur->right,count);
// 恢复目标值,为后续节点做准备
count+=cur->right->val;
// 从当前路径中移除最后一个元素,为后续遍历做准备
path.pop_back();
}
return; // 结束此方法
}
// 定义一个公有方法,接收二叉树的根节点和目标总和作为参数,并返回满足条件的路径列表
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
// 如果根节点为空,直接返回结果列表(空列表)
if(root==NULL) return ans;
// 将当前节点的值添加到当前路径中
path.push_back(root->val);
// 减少目标值,因为当前节点的值会被加到子树的和中(但这个值是0,所以实际上没有影响)
traversal(root,targetSum-root->val);
// 结束后返回结果列表
return ans;
}
}; c++优化代码
class Solution {
public:
vector<vector<int>> ans; // 存放最终结果的二维数组
vector<int> path; // 存放当前路径的数组
void traversal(TreeNode *cur, int targetSum) {
if (!cur) return; // 当前节点为空,直接返回
path.push_back(cur->val); // 将当前节点的值加入路径数组
targetSum -= cur->val; // 更新目标和
if (!cur->left && !cur->right && targetSum == 0) { // 当前节点是叶子节点,且路径和等于目标和
ans.push_back(path); // 将当前路径加入结果数组
} else {
traversal(cur->left, targetSum); // 继续遍历左子树
traversal(cur->right, targetSum); // 继续遍历右子树
}
path.pop_back(); // 回溯操作,将当前节点从路径数组中弹出
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
traversal(root, targetSum); // 从根节点开始遍历,并计算路径和
return ans; // 返回结果数组
}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。