目录
- 用set而非list进行查找
- 用dict而非两个list进行匹配查找
- 优先使用for循环而不是while循环
- 循环代替递归
- 用缓存机制加速递归函数
- 用numba加速Python函数
- 使用collections.Counter加速计数
- 使用collections.ChainMap加速字典合并
- 使用map代替推导式进行加速
- 使用filter代替推导式进行加速
- 多线程加速IO密集型任务
- 应用多进程加速CPU密集型任务
用set而非list进行查找
列表是一个有序的可重复元素的集合,它可以包含任意类型的对象。列表的实现通常使用动态数组,这意味着可以通过索引来快速访问元素。
集合是一个无序的不重复元素的集合,它只能包含可散列的对象(例如,数字、字符串等)。集合的实现通常使用哈希表或类似的数据结构,这使得它能够在O(1)的时间复杂度内查找元素。
由于集合使用哈希表实现,它可以在常数时间内(O(1))执行查找操作,而列表需要在最坏情况下遍历整个列表才能找到目标元素,其时间复杂度为O(n)。
集合是用来存储唯一元素的,所以在查找时,它不需要考虑是否有重复的元素,这也使得它在查找时更加高效。
list_d = [x**2 + 1 for x in range(1000000)]
set_d = (x**2 + 1 for x in range(1000000))
# 慢
1098987 in list_d
# 快
1098987 in set_d
用dict而非两个list进行匹配查找
看如下例子:
list_a = [2*i - 1 for i in range(1000000)]
list_b = [i**2 for i in list_a]
# 列表查找
print(list_b[list_a.index(876567)])
# 使用字典按照key查找
dict_ab = dict(zip(list_a, list_b))
print(dict_ab.get(876567, None))
与set同理,dict也是使用哈希表实现,也可以在常数时间内(O(1))执行查找操作。
优先使用for循环而不是while循环
示例:
import time
def time_cal(func):
def wrapper():
t1 = time.time()
func()
print(f"耗时:{time.time() - t1}")
return wrapper
@time_cal
def func1():
s = 0
i = 0
while s < 10000:
s += 1
i += 1
@time_cal
def func2():
s = 0
for i in range(10000):
s += 1
if __name__ == "__main__":
func1()
func2()
结果如下:
耗时:0.0007779598236083984
耗时:0.00047516822814941406
循环代替递归
示例如下:
import time
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
def func1(n):
# 斐波那契函数
return (1 if n in (1, 2) else (func1(n-1) + func1(n-2)))
@time_cal
def func2(n):
if n in (1, 2):
return 1
a, b = 1, 1
for i in range(2, n):
a, b = b, a + b
return b
if __name__ == "__main__":
t1 = time.time()
func1(30)
print(f"耗时:{time.time() - t1}")
func2(30)
结果如下:
耗时:0.1676180362701416
耗时:7.867813110351562e-06
递归虽然简单,但是可能存在以下问题:
- 在递归中,每次函数调用都会涉及到压栈和弹栈的操作,这会导致额外的开销。每次函数调用都需要保存当前函数的状态(包括局部变量、返回地址等),而循环则避免了这种开销。
- 另外有最大的函数调用栈深度限制。当递归的深度超过这个限制时,会引发栈溢出错误。
- 一些编译器可以对尾递归做出优化,将其转换为类似循环的形式,从而避免了递归的开销。
- 在一些问题中,递归可能会导致重复计算,因为递归往往会反复调用相同的子问题,而迭代可以使用循环变量来避免这种情况。
用缓存机制加速递归函数
上面说到,递归可能会导致重复计算,会反复调用相同的子问题。可以使用缓存减少重复计算。
代码如下:
import time
from functools import lru_cache
@lru_cache(100)
def func1(n):
# 斐波那契函数
return (1 if n in (1, 2) else (func1(n-1) + func1(n-2)))
if __name__ == "__main__":
t1 = time.time()
func1(30)
print(f"耗时:{time.time() - t1}")
执行时间如下:
耗时:1.3828277587890625e-05
可以看到时间明显少了几个数量级。
用numba加速Python函数
未加速的代码:
import time
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
def my_power(x):
return x**2
@time_cal
def my_power_sum(n):
s = 0
for i in range(1, n+ 1):
s += my_power(i)
return s
if __name__ == "__main__":
my_power_sum(1000000)
执行时间如下:
耗时:0.324674129486084
使用numba如下:
import time
from numba import jit
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
@jit
def my_power(x):
return x**2
@time_cal
@jit
def my_power_sum(n):
s = 0
for i in range(1, n+ 1):
s += my_power(i)
return s
if __name__ == "__main__":
my_power_sum(1000000)
执行时间:
耗时:0.25246715545654297
使用collections.Counter加速计数
示例如下:
import time
from collections import Counter
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
@time_cal
def func1(data):
# 普通方法
values_count = {}
for i in data:
i_count = values_count.get(i, 0)
values_count[i] = i_count + 1
print(values_count.get(4, 0))
@time_cal
def func2(data):
# 加速方法
values_count = Counter(data)
print(values_count.get(4, 0))
if __name__ == "__main__":
data = [x**2 % 1989 for x in range(2000000)]
func1(data)
func2(data)
运行结果如下:
8044
耗时:0.27747488021850586
8044
耗时:0.14070415496826172
使用collections.ChainMap加速字典合并
示例如下:
import time
from collections import ChainMap
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
@time_cal
def func1(dic_a, dic_b, dic_c, dic_d):
# 普通方法
res = dic_a.copy()
res.update(dic_b)
res.update(dic_c)
res.update(dic_d)
print(res.get(9999, 0))
@time_cal
def func2(dic_a, dic_b, dic_c, dic_d):
# 加速方法
chain = ChainMap(dic_a, dic_b, dic_c, dic_d)
print(chain.get(9999, 0))
if __name__ == "__main__":
dic_a = {i: i + 1 for i in range(1, 1000000, 2)}
dic_b = {i: 2*i + 1 for i in range(1, 1000000, 3)}
dic_c = {i: 3*i + 1 for i in range(1, 1000000, 5)}
dic_d = {i: 4*i + 1 for i in range(1, 1000000, 7)}
func1(dic_a, dic_b, dic_c, dic_d)
func2(dic_a, dic_b, dic_c, dic_d)
运行结果如下:
10000
耗时:0.05382490158081055
10000
耗时:4.57763671875e-05
使用map代替推导式进行加速
示例如下:
import time
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
@time_cal
def func1():
# 普通方法
res = [x**2 for x in range(1, 1000000, 3)]
@time_cal
def func2():
# 加速方法
res = map(lambda x: x**2, range(1, 1000000, 3))
if __name__ == "__main__":
func1()
func2()
运行结果如下:
耗时:0.0947120189666748
耗时:1.0013580322265625e-05
使用filter代替推导式进行加速
示例如下:
import time
def time_cal(func):
def wrapper(*args, **kwargs):
t1 = time.time()
func(*args, **kwargs)
print(f"耗时:{time.time() - t1}")
return wrapper
@time_cal
def func1():
# 普通方法
res = [x**2 for x in range(1, 1000000, 3) if x % 7 == 0]
@time_cal
def func2():
# 加速方法
res = filter(lambda x: x%7 == 0, range(1, 1000000, 3))
if __name__ == "__main__":
func1()
func2()
运行如下:
耗时:0.03171205520629883
耗时:1.0013580322265625e-05
多线程加速IO密集型任务
低速方法
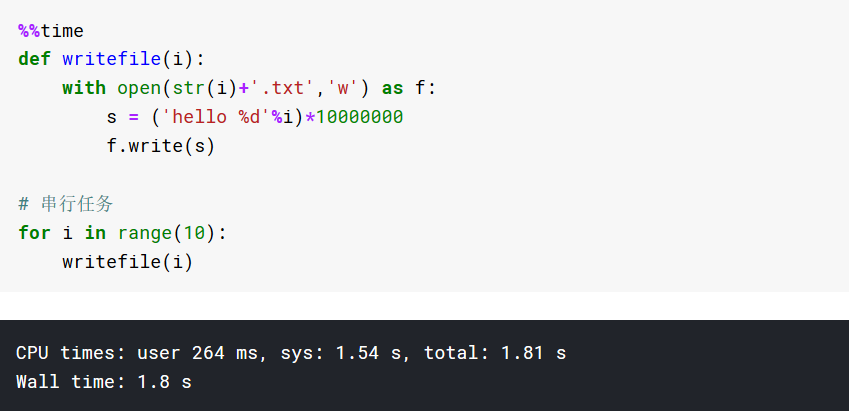 高速方法
高速方法
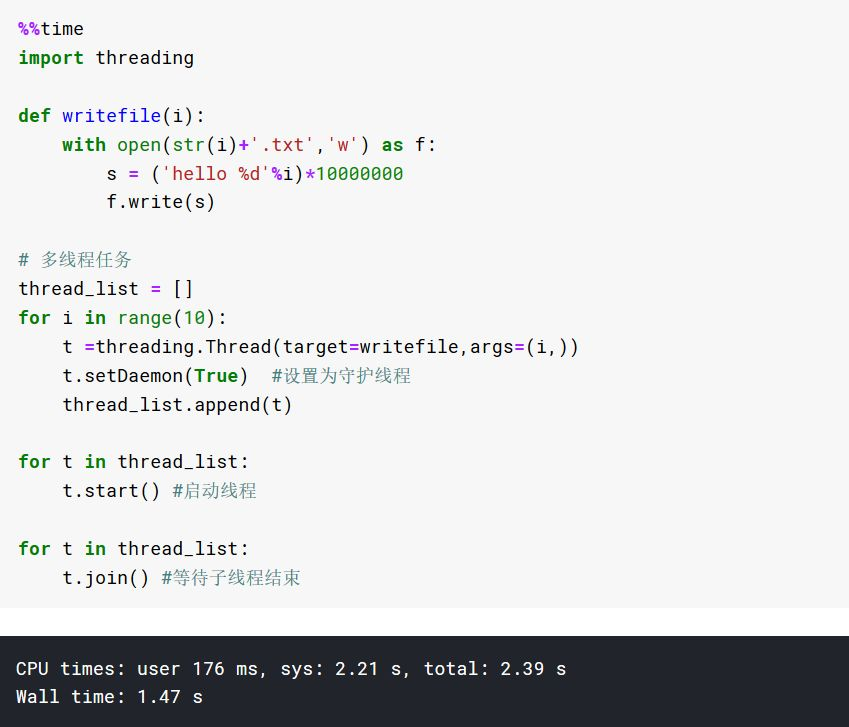
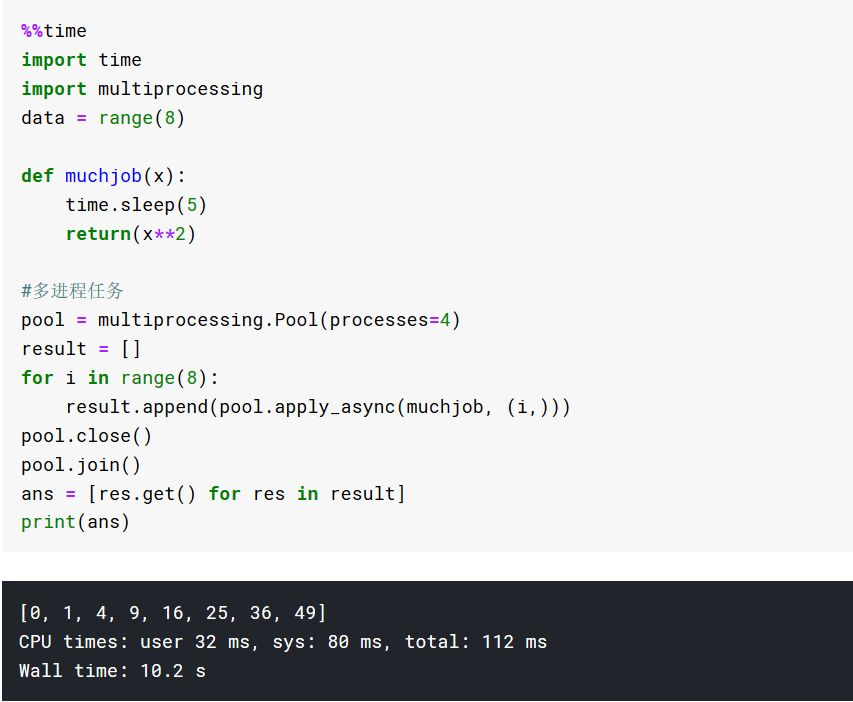
应用多进程加速CPU密集型任务
低速方法
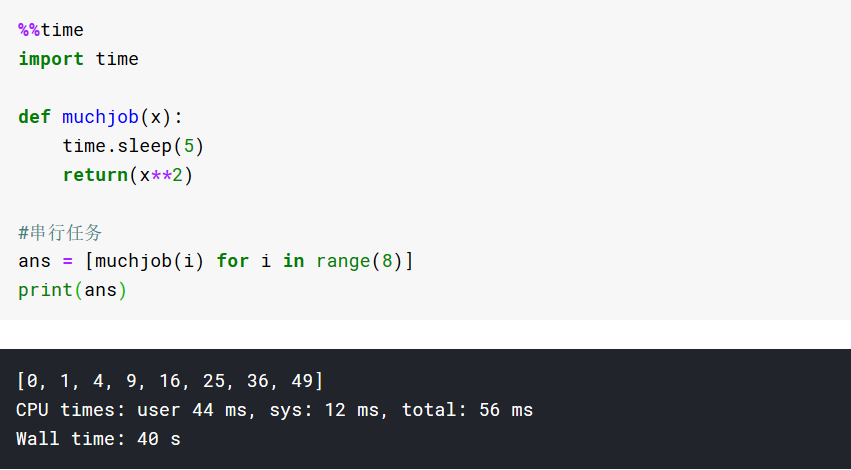
高速方法
参考:
https://mp.weixin.qq.com/s/oF35_g4gdPeprHSvw4Mnyg