数据结构基本概念-Java常用算法
- 1、数据结构基本概念
- 2、数据逻辑结构
- 3、算法时间复杂度
1、数据结构基本概念
- 数据(Data):数据是信息的载体,其能够被计算机识别、存储和加工处理,是计算机程序加工的“原材料”。
- 数据元素(Data Element):数据元素是数据的基本单位,其也称元素、结点、顶点、记录等。一般来说,一个数据元素可以由若干个数据组成,数据项是具有独立含义的最小标识单位。数据项也可称为字段、域、属性等。
- 数据结构(Data Structure):数据结构指的是数据之间的相互关系,也就是数据的组织形式。
数据结构的内容:
- 数据的逻辑结构: 线性结构、树型结构、图结构
- 数据的存储结构: 顺序存储、链式存储
- 数据操作: 也就是数据的运算,基于数据的逻辑结构上,最常用的运算包括检索、插入、删除、更新、排序等。
数据类型:通常是指高级程序设计语言支持的基本数据类型,如C/C++、Java、Python、Kotlin等。
抽象数据类型:数据的组织,及其相关的操作。
2、数据逻辑结构
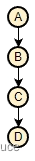
线性结构: 除第一个和最后一个数据元素外,每个数据只有一个唯一的前驱数据元素和一个唯一个的后驱数据元素。
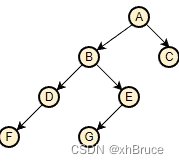
树型结构: 除根节点外,每个数据元素只有一个唯一的前驱数据元素,可有零个或若干个后驱数据元素。
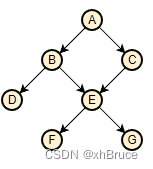
图型结构: 每个数据元素可有零个或若干个前驱数据元素和零个或若干个后驱数据元素。
3、算法时间复杂度
算法时间复杂度:算法的耗时与算法所处理的数据个数 n 的函数关系的分析;主要分析算法的耗时与算法处理数据个数 n 的 数量级 意义上的函数关系。
算法的时间复杂度与空间复杂度通常是矛盾的。目前计算机内存下降趋势下,当发生矛盾时,对于大多数情况来说,算法的时间复杂度应首先被考虑。
【定义】 T ( x ) = O ( f ( n ) ) T(x) = O(f(n)) T(x)=O(f(n))当且仅当存在正常数 c c c和 n 0 n_{0} n0,对所有的 n ( n ≥ n 0 ) n(n\ge n_{0} ) n(n≥n0)满足 T ( n ) ≤ c f ( n ) T(n)\le cf(n) T(n)≤cf(n)。
当算法的时间复杂度 T ( n ) T(n) T(n)和数据个数 n n n无关系时, T ( n ) ≤ c × 1 T(n) \le c\times 1 T(n)≤c×1,所以此时算法的时间复杂度 T ( n ) = O ( 1 ) T(n) = O(1) T(n)=O(1);
当算法的时间复杂度 T ( n ) T(n) T(n)和数据个数 n n n为线性关系时, T ( n ) ≤ c n T(n)\le cn T(n)≤cn,所以此时算法的时间复杂度 T ( n ) = O ( n ) T(n) = O(n) T(n)=O(n);
当算法的时间复杂度 T ( n ) T(n) T(n)和数据个数 n n n为平方关系时, T ( n ) ≤ c n 2 T(n)\le cn^2 T(n)≤cn2,所以此时算法的时间复杂度 T ( n ) = O ( n 2 ) T(n) = O(n^2) T(n)=O(n2);
依次类推,还有 O ( n 3 ) O(n^3) O(n3)、 O ( log 2 n ) O(\log_{2}{n}) O(log2n)、 O ( lg n ) O(\lg_{}{n}) O(lgn)、 O ( lg n ) O(\lg_{}{n}) O(lgn)、 O ( 2 n ) O(2^n) O(2n)等
算法的时间复杂度是衡量一个算法好坏的重要指标。一般来说,具有多项式时间复杂度(如 O ( n ) O(n) O(n)、 O ( n 2 ) O(n^2) O(n2)、 O ( n 6 ) O(n^6) O(n6)等)的算法,是可以接收的、可实际使用的算法;而具有指数时间复杂度(如 O ( 2 n ) O(2^n) O(2n)、 O ( n n ) O(n^n) O(nn)、 O ( n ! ) O(n!) O(n!)等)的算法,是理论上可以计算,但实际上不可计算的问题,通常称作难解的问题。
i i i n n n n 2 n^2 n2 n 3 n^3 n3 2 n 2^n 2n n ! n! n! n n n^n nn 1 1 1 1 2 1 1 2 2 4 8 4 2 4 3 3 9 27 8 6 27 … … … … … … … 10 10 100 1000 1024 3628800 1.9 × 1 0 10 1.9\times 10^{10} 1.9×1010 … … … … … … … 20 20 400 8000 1048376 2.4 × 1 0 18 2.4\times 10^{18} 2.4×1018 1.0 × 1 0 25 1.0\times 10^{25} 1.0×1025 … … … … … … … 100 100 10000 1.0 × 1 0 6 1.0\times 10^{6} 1.0×106 1.3 × 1 0 30 1.3\times 10^{30} 1.3×1030 9.3 × 1 0 157 9.3\times 10^{157} 9.3×10157 1.0 × 1 0 200 1.0\times 10^{200} 1.0×10200 通常当基本语句计算次数超过 1.0 × 1 0 15 1.0\times 10^{15} 1.0×1015次时,该算法的计算机执行时间就比较长。设 计算机每秒可执行1亿次( 1.0 × 1 0 9 1.0\times 10^{9} 1.0×109)条基本语句 ,则执行一个需要 1.0 × 1 0 15 1.0\times 10^{15} 1.0×1015次基本操作的算法时间为:
T = ( 1.0 × 10 15 ) / ( 1.0 × 10 9 ) = 1.0 × 10 6 ( 秒 ) T = (1.0\times {10}^{15}) / (1.0\times {10}^{9}) = 1.0\times {10}^{6}(秒) T=(1.0×1015)/(1.0×109)=1.0×106(秒)
= ( 1.0 × 10 6 ) / 3600 = 277.8 ( 天 ) = (1.0\times {10}^{6}) / 3600 = 277.8(天) =(1.0×106)/3600=277.8(天)
= 277.8 / 24 = 11.6 ( 天 ) = 277.8 / 24 = 11.6(天) =277.8/24=11.6(天)