优先级队列
- 基本使用
- 题目训练
基本使用
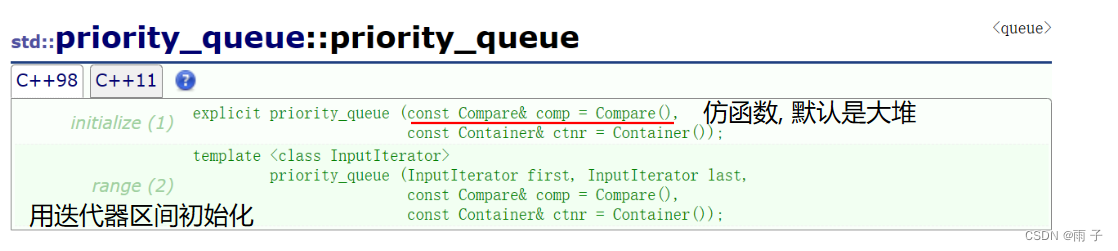
priority_queue, 优先级队列, 又叫做双端队列, 头文件也是 <queue>
别看它叫做队列, 其实它是一个 堆
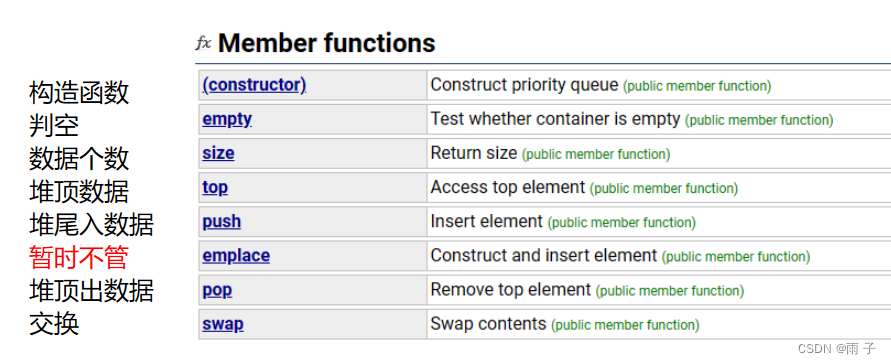
补充一下概念:
- 大根堆 — — 每一棵树的父节点比它的孩子都大
- 小跟堆 — — 每一棵树的父节点比它的孩子都小
👇👇👇
void test()
{
// 默认构建的是一个大堆
priority_queue<int> pq;
pq.push(1);
pq.push(5);
pq.push(4);
pq.push(9);
pq.push(10);
pq.push(6);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
}
int main()
{
test();
return 0;
}
运行结果:
10 9 6 5 4 1
注意:
不要被这里的按序输出迷惑了,
优先级队列的内部结构是堆, 堆的内部结构是不一定按照元素的顺序排列的。
- 那如果我们要
小跟堆输出呢?
void test()
{
// 仿函数控制, greater是构建小跟堆
priority_queue<int,vector<int>, greater<int> > pq;
pq.push(1);
pq.push(6);
pq.push(20);
pq.push(15);
pq.push(8);
pq.push(2);
pq.push(6);
pq.push(4);
pq.push(9);
pq.push(10);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
}
int main()
{
test();
return 0;
}
运行结果:
1 2 4 6 6 8 9 10 15 20
- 要构建小跟堆, 我们要用
greater - 由于仿函数是最后一个参数, 那么处于中间位置的
容器适配器也要给个参数
如何使用
- 使用迭代区间初始化
void test()
{
vector<int> vec;
vec.push_back(1);
vec.push_back(2);
vec.push_back(9);
vec.push_back(8);
vec.push_back(7);
priority_queue<int> pq(vec.begin(), vec.end());
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
int main()
{
test();
return 0;
}
运行结果:
9 8 7 2 1
当然我们也可以 建小堆
void test()
{
vector<int> vec;
vec.push_back(1);
vec.push_back(2);
vec.push_back(9);
vec.push_back(8);
vec.push_back(7);
priority_queue<int,vector<int>, greater<int> > pq(vec.begin(), vec.end());
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
int main()
{
test();
return 0;
}
运行结果:
1 2 7 8 9
题目训练
- 数组中的第K个最大元素

这是我们熟悉的 TopK问题.
那么问题来了, 要求时间复杂度是 O(n), 我们是建小堆还是大堆呢?
其实, 建小堆 和 建大堆都是一样的
- 建大堆
- 建大堆 — — 时间复杂度是
O(n) - pop (k-1) 次 — — 向上调整算法, 时间复杂度是
O(logN) - 堆顶元素就是答案
- 建大堆 — — 时间复杂度是
总体的时间复杂度是 O(n)
class Solution {
public:
int findKthLargest(vector<int>& nums, int k)
{
// 1. 建大堆
// 建堆 -- O(n)
priority_queue<int> pq(nums.begin(), nums.end());
// 2. pop(k-1)次
// pop, 向上调整算法 -- O(logN)
while(--k)
{
pq.pop();
}
return pq.top();
}
};
- 建小堆
- 建一个
个数为K的小堆— — 时间复杂度是O(K) - 将剩余元素中的
大于堆顶元素的数据 插入堆中— — 时间复杂度是(N-K)l ogK
1. 如果 K很大, 那么时间复杂度是O(log K)
2. 如果 K很小, 那么时间复杂度是O(N) - 返回堆顶元素
- 建一个
总体的时间复杂度是 O(n)
class Solution {
public:
int findKthLargest(vector<int>& nums, int k)
{
// 1. 建小堆
// 建堆 -- O(n)
priority_queue<int, vector<int>, greater<int> > pq(nums.begin(), nums.begin()+k);
// 2. pop
// pop, 向上调整算法 -- O((N-K) logK)
// push, 向上调整算法 -- O((N-K) logK)
for(int i = k; i < nums.size(); i++)
{
if(nums[i] > pq.top())
{
pq.pop();
pq.push(nums[i]);
}
}
return pq.top();
}
};
弟子曰:此学甚好,只是簿书讼狱繁难,不得为学。
阳明曰:簿书讼狱之间,无非实学;若离了事物为学,却是着空。
译文:
弟子说:先生的学问很好,但是平时工作太忙了,没空修习。
先生说:学问不能脱离工作,在工作中修行,才是真正的学习。如果脱离了实际事务,那修行就没用了。
王阳明认为:工作就是最好的修行。
把工作中遇到的烦恼,当成磨炼自己心性的机会;
把工作中的怠惰懒散,当成改变自己态度的试炼;
把工作中的愤怒委屈,当成放大格局的磨砺。
稻盛和夫说:工作中修行,是帮助我们提升心性和培养人格的最重要、也是最有效的方法。
工作是用,修身是体 ,用成长的心态去工作,就是一个人最好的修行。