16数据处理

news2025/11/4 16:33:55

plotly

设置x/y轴名称

yaxis_title=‘金额(元)’,xaxis_title=‘日期’

fig = px.line(df_grouped, x="Order_time", y="Money", title='日销图')
fig.update_layout(yaxis_title='金额(元)',xaxis_title='日期', xaxis_tickformat='%Y-%m-%d',yaxis_tickformat = '0.2f')
fig.show()

设置x/y轴范围

fig.update_layout(yaxis_title='loss',xaxis_title='epochs',yaxis_tickformat = '0.3f',
                  #全闭区间0-61
                  xaxis_range=[0,61]
                 )

调整日期格式

xaxis_tickformat='%Y-%m-%d

# 画图展示每日销量
fig = px.line(df_grouped, x="Order_time", y="Money", title='日销图')
fig.update_layout(yaxis_title='金额(元)',xaxis_title='日期', xaxis_tickformat='%Y-%m-%d',yaxis_tickformat = '0.2f')
fig.show()

设置数值保留小数

yaxis_tickformat = ‘0.2f’

# 画图展示每日销量
fig = px.line(df_grouped, x="Order_time", y="Money", title='日销图')
fig.update_layout(yaxis_title='金额(元)',xaxis_title='日期', xaxis_tickformat='%Y-%m-%d',yaxis_tickformat = '0.2f')
fig.show()

基础折线图

import plotly.express as px
# 画图展示每日销量
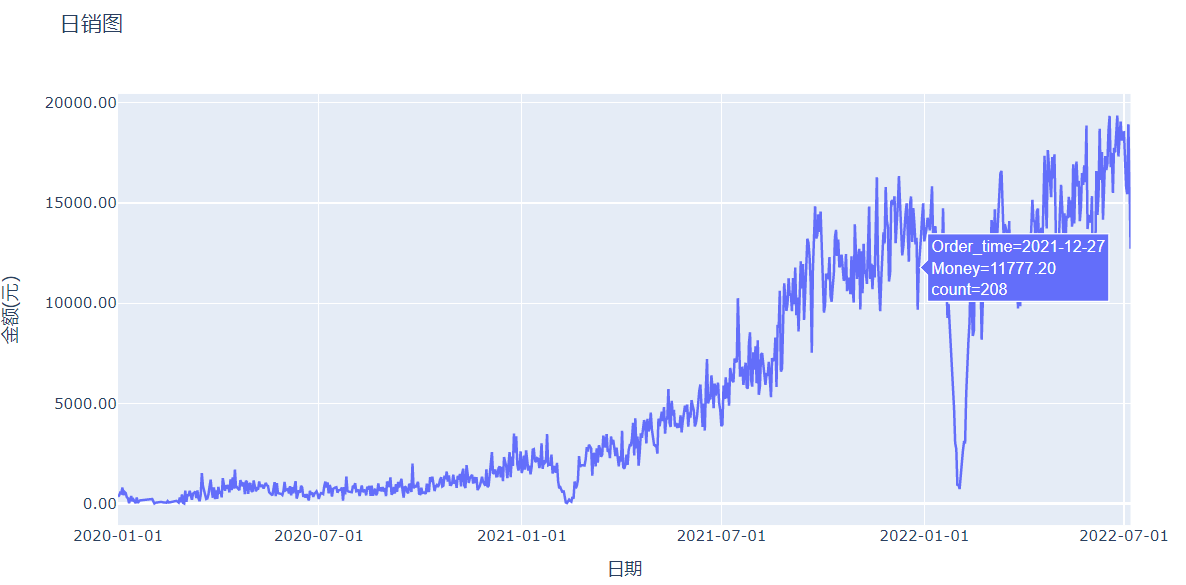
fig = px.line(df_final, x="Order_time", y="Money", title='日销图',hover_data=['count'])
fig.update_layout(yaxis_title='金额(元)',xaxis_title='日期', xaxis_tickformat='%Y-%m-%d',yaxis_tickformat = '0.2f')
fig.show()

image-20230208160608748

去除网格

fig = go.Figure()
fig.update_layout(yaxis_title='loss',xaxis_title='epochs',yaxis_tickformat = '0.2f',xaxis_showgrid=False, yaxis_showgrid=False)

设置背景颜色

fig.update_layout(yaxis_title='loss',xaxis_title='epochs',yaxis_tickformat = '0.2f',xaxis_showgrid=False, yaxis_showgrid=False,paper_bgcolor='white',plot_bgcolor='rgb(243, 243, 243)')

一图多表

https://plotly.com/python/reference/scatter/

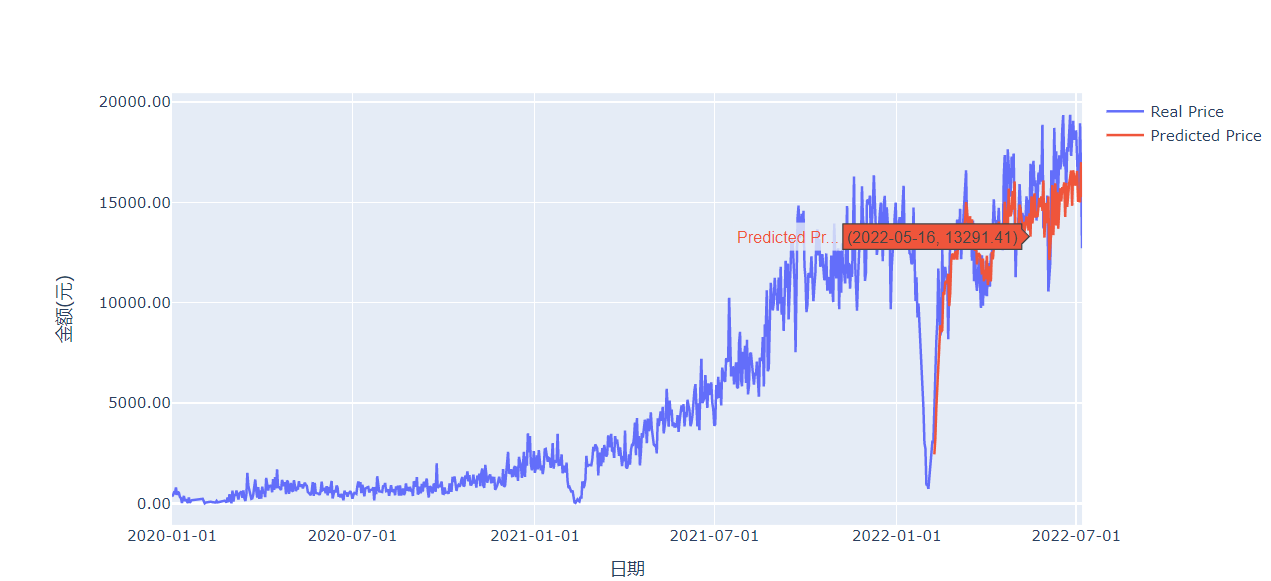
示例1

import plotly.graph_objects as go
fig = go.Figure()
fig.update_layout(yaxis_title='金额(元)',xaxis_title='日期', xaxis_tickformat='%Y-%m-%d',yaxis_tickformat = '0.2f')

fig.add_trace(go.Scatter(
    x=df_final_no_index['Order_time'],
    y=df_final_no_index['Money'],
    name = 'Real Price',
    # 设定图像的形式
    mode = 'lines',
    # 在marker中设置图像的颜色
#    marker = dict(
#         color = 'skyblue'，
#		  size =5,
#		  symbol = 'circle/square/x'
#     )
))
fig.add_trace(go.Scatter(
    x=df_final_no_index['Order_time'][-(test_split-30):],
    y=pred,
    name = 'Predicted Price',
    mode = 'lines'
))

fig.show()

image-20230208133737430

示例2：

import plotly.graph_objects as go
fig = go.Figure()
fig.update_layout(yaxis_title='充值分数',xaxis_title='消费分数',yaxis_tickformat = '0.2f',title = '分类结果')

fig.add_trace(go.Scatter(
    x=total_data['consume_score'],
    y=total_data['recharge_score'],
    name = '用户分数',
    # 设定图像的形式
    mode = 'markers',
    marker = dict(
        color = total_data['prediction'],
        colorscale = 'Viridis'
    )
))
fig.add_trace(go.Scatter(
    x=centers['x'],
    y=centers['y'],
    name = '质心',
    mode = 'markers',
    marker = dict(
        size = 10,
        symbol = 'x'
    )
))

fig.show()

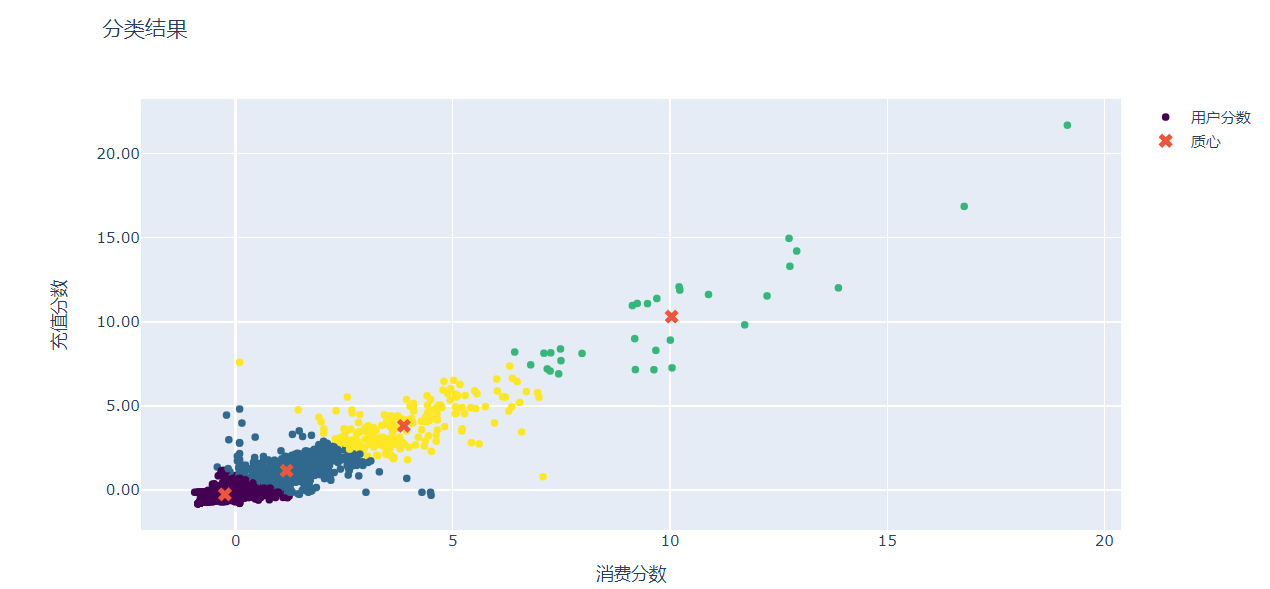
image-20230208142305538

显示额外数据

hover_data

fig = px.line(df_final, x="Order_time", y="Money", title='日销图',hover_data=['count'])

pandas

索引

删除索引

df_final.reset_index(drop=False,inplace=True)

添加索引

df_final.set_index('Order_time',inplace=True)

分组及聚合操作

求和

# 按照日期分组并求和，会对能够计算的列进行求和  numeric_only防止警告
df_grouped_sum = df_clear.groupby(by=df_clear['Order_time'].dt.date).sum(numeric_only = True)

计数

# 按照日期分组并计数 会对所有列进行计数
df_grouped_count = df_clear.groupby(by=df_clear['Order_time'].dt.date).count()

ndarray转dataframe

array_1 = np.array([1, 2, 3, 4])
df_1 = pd.DataFrame(array_1, columns=["Column 1"])

concat根据索引合并

import numpy as np
import pandas as pd
# Create two ndarrays
array_1 = np.array([1, 2, 3, 4])
array_2 = np.array([5, 6, 7, 8])

# Convert ndarrays to DataFrames
df_1 = pd.DataFrame(array_1, columns=["Column 1"])
df_2 = pd.DataFrame(array_2, columns=["Column 2"])

# Concatenate DataFrames along columns (axis=1)
df_merged = pd.concat([df_1, df_2], axis=1)

print(df_merged)

修改列类型

older['Order_time'] = older['Order_time'].astype('str')

按列赋值

# 其中pred是ndarray类型也可以 df类型就指定列即可
df_test_predict['Money'] = pred

merge根据字段合并

In [33]: left = pd.DataFrame(
   ....:     {
   ....:         "key": ["K0", "K1", "K2", "K3"],
   ....:         "A": ["A0", "A1", "A2", "A3"],
   ....:         "B": ["B0", "B1", "B2", "B3"],
   ....:     }
   ....: )
   ....: 

In [34]: right = pd.DataFrame(
   ....:     {
   ....:         "key": ["K0", "K1", "K2", "K3"],
   ....:         "C": ["C0", "C1", "C2", "C3"],
   ....:         "D": ["D0", "D1", "D2", "D3"],
   ....:     }
   ....: )
   ....: 

In [35]: result = pd.merge(left, right, on="key")

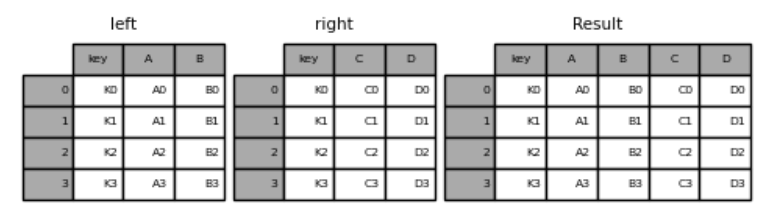
image-20230208163637815

读取文件

excel

df=pd.read_excel("data/Data003_SelfOperate.xlsx",parse_dates=["Order_time"])

查看数据范围

df.describe().loc[['min', 'max']]

去除时分秒

df["Order_time"] = df["Order_time"].dt.date

过滤数据

# 过滤金额范围
df = df[(df['Money']>=5)&(df['Money']<=10000)]
# 过滤时间段为[2020-1-1:]
df['Order_time'] = pd.to_datetime(df['Order_time'])
df = df[(df['Order_time'] >= pd.Timestamp('2020-01-01'))]

选择多列

df_clear = df[['Order_time','Money']]

插入新列

df.insert(loc=2, column='c', value=3)  # 在最后一列后，插入值全为3的c列

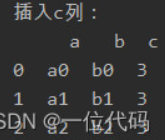
image-20230209205658804

保留小数

df_merged['predicted_price'] = df_merged['predicted_price'].apply(lambda x: round(x, 2))

生成时间序列

pd_day = pd.date_range('20220708',periods=30,freq='D')

eg:

需求：在已有日期df_for_predict后加入新增的时间序列

# 创建空的数组
# empty = np.zeros((future_span,1))
# ndarray 转 pd
# future = pd.DataFrame(empty,columns = ['Money'])
# 生成时间序列
pd_day = pd.date_range('20220708',periods=future_span,freq='D')
# ndarray 转 pd
older = pd.DataFrame(pd_day,columns=['Order_time'])
# 时间类型转换成字符串
older['Order_time'] = older['Order_time'].astype('str')
# older.set_index('Order_time',inplace=True)
# 插入money列
older.insert(loc=1, column='Money', value=0)
# 按行连接两个表
df_for_predict = pd.concat([df_for_predict,older])
df_for_predict.set_index('Order_time',inplace=True)
df_for_predict.tail(20)

machine learning

激活函数 activation

作用

​ 一个没有激活函数的神经网络将只不过是一个线性回归模型（Linear regression Model）罢了，它功率有限，并且大多数情况下执行得并不好。

​ 将模型中一个节点的输入信号转换成一个输出信号,这使得模型可以学习和模拟其他复杂类型的数据。

比如逻辑回归中 z = w x + b z=wx+b z=wx+b

而激活函数的输入为z : f ( z ) = s i g m o i d f u n c t i o n = 1 1 + e − z f(z)=sigmoid function=\frac{1}{1+e^{-z}} f(z)=sigmoidfunction=1+e−z1​

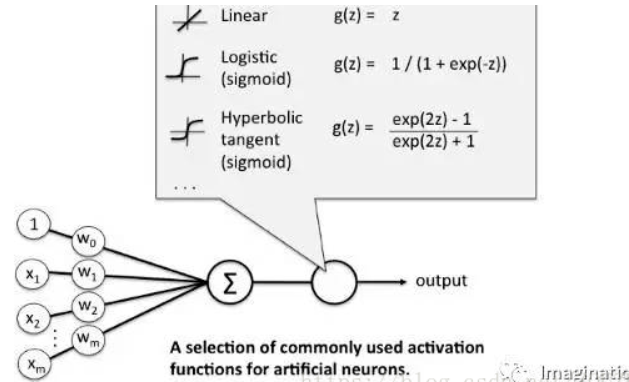
image-20230206145027283

如何选择

  1. 在深度学习的隐藏层中，一般使用relu
  2. 在输出层，取决于标签值y
    1. y=0/1 ——sigmoid
    2. y可正可负——linear
    3. y$>=$0——relu

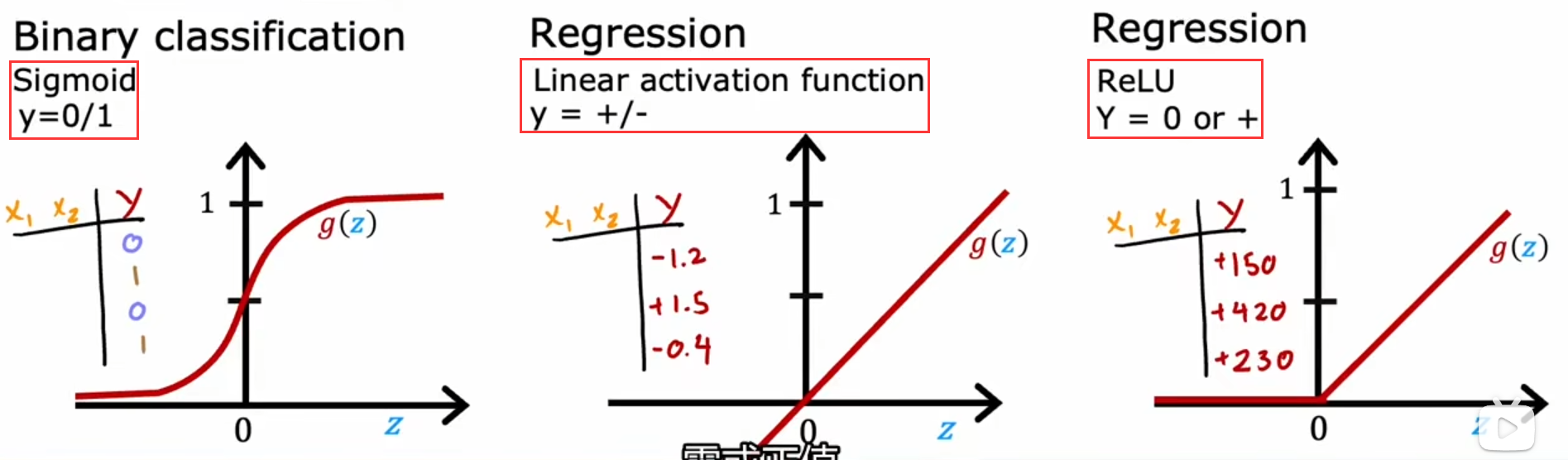
image-20230206143833728

loss函数和cost函数

loss:用来计算预测值与真实值之间的差异，是单个样本的值

比如逻辑回归中使用的交叉熵函数：

image-20230206150102582

以及非逻辑回归的均方差函数：

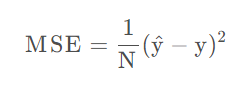
​ image-20230207120047514

cost:整个训练集上loss的平均值

模型的最终目的就是尽可能使cost函数最小化

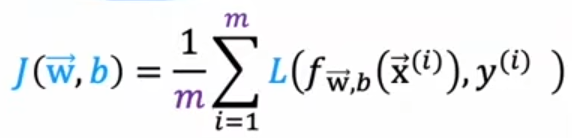
image-20230206150424291

loss值和val_loss值

loss和val loss 的区别：
  loss：训练集整体的损失值。
  val loss：验证集（测试集）整体的损失值。
loss和val loss，两者之间的关系：
  当loss下降，val_loss下降：训练正常，最好情况。

  1. 当loss下降，val_loss稳定：网络过拟合化。这时候可以添加Dropout和Max pooling。
  2. 当loss稳定，val_loss下降：说明数据集有严重问题，可以查看标签文件是否有注释错误，或者是数据集质量太差。建议重新选择。
  3. 当loss稳定，val_loss稳定：学习过程遇到瓶颈，需要减小学习率（自适应网络效果不大）或batch数量。
  4. 当loss上升，val_loss上升：网络结构设计问题，训练超参数设置不当，数据集需要清洗等问题，最差情况

梯度下降

梯度下降法(alpha 为学习率):

image-20230206150558071

学习率

影响的是梯度下降的过程

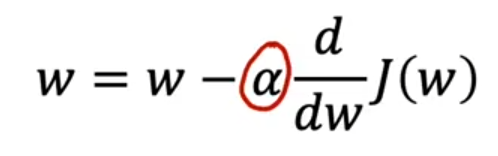
image-20230210164318245

过小：导致梯度下降过程缓慢

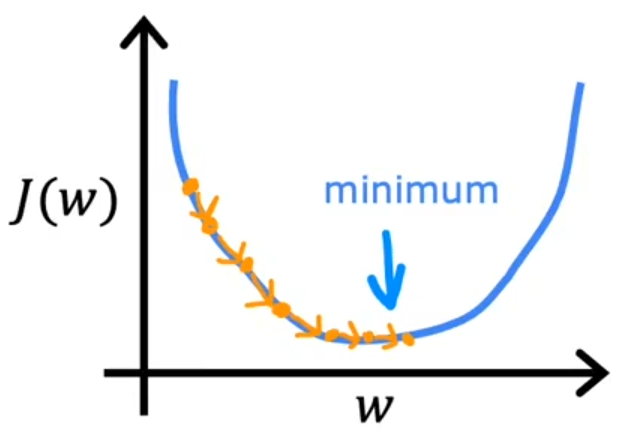
image-20230210164336392

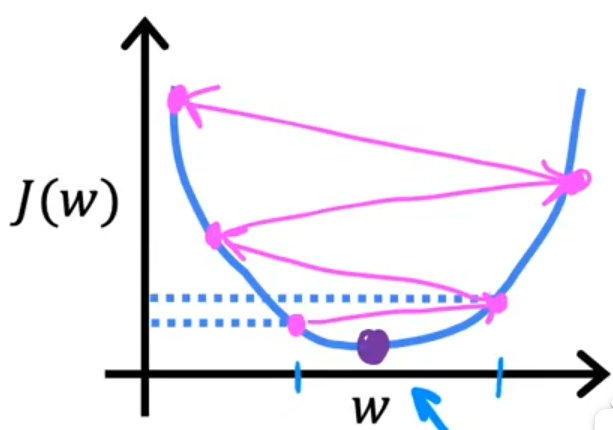
过大：可能永远达不到梯度的最小值

image-20230210164530733

过拟合

解决方法

  1. 收集更多数据
  2. 不要使用太多特征
  3. 正则化

正则化

核心：尽可能地减小w(权重)，与直接删除某些特征值的做法相比，他更加温和

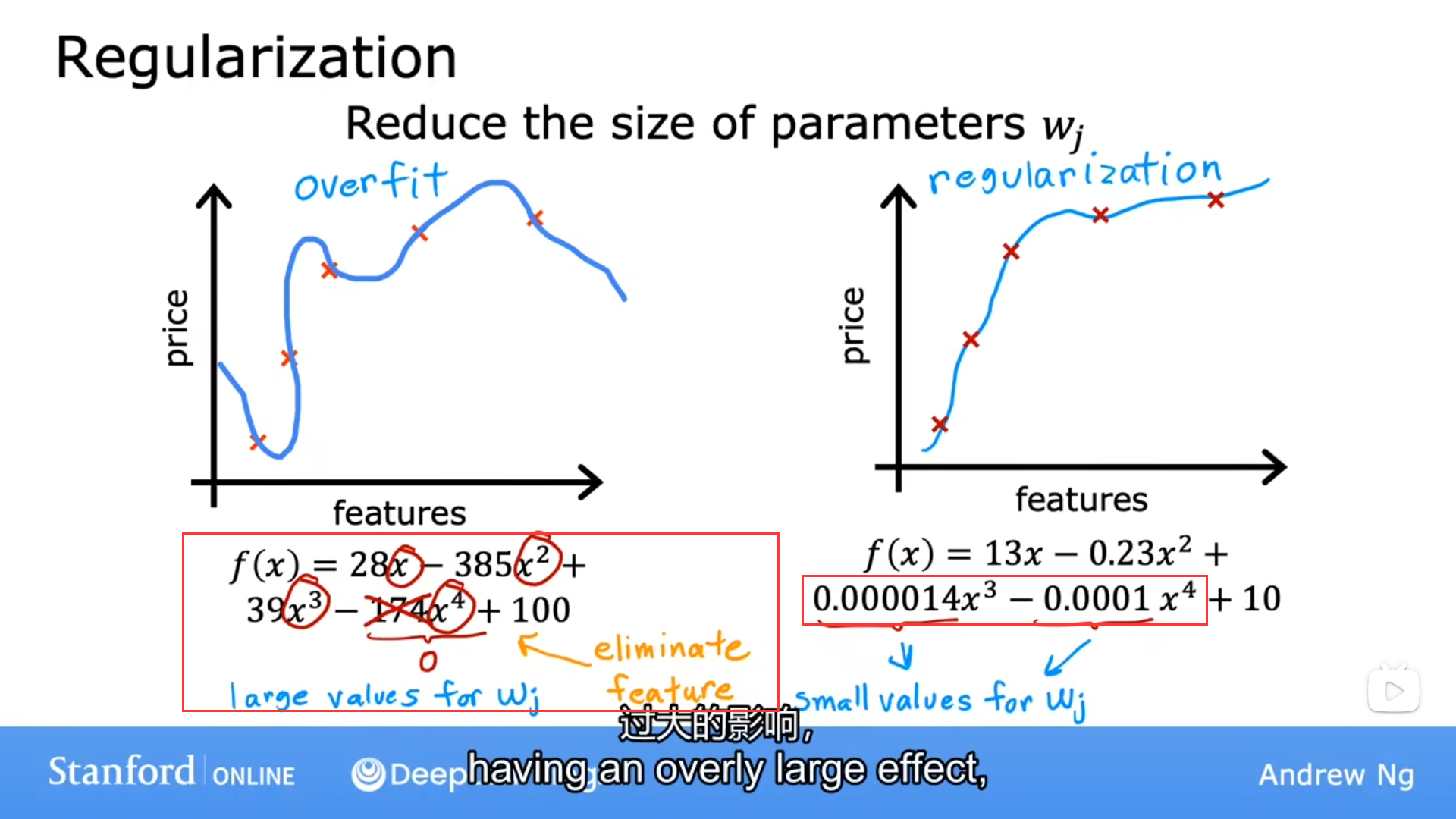
image-20230206153959714

原理

目的是最小化代价函数J(w,b)

image-20230206154624358

  1. λ = 0 \lambda=0 λ=0:相当于没有正则化
  2. λ 过大 \lambda过大 λ过大:要使得J尽可能小，那么w就尽可能小，因为他前面的系数 λ \lambda λ很大，导致w近似为0，出现欠拟合

image-20230206155349789

image-20230206160518556

所以 λ \lambda λ需要有合理的取值范围，通常为[1,10]

tensorflow

一般步骤

以逻辑回归为例，使用tf构造神经网络的步骤和机器学习中的步骤一样

  1. 构造模型
  2. 选取loss函数
  3. 评估

image-20230206150939856

举例

  • 定义模型

image-20230206151912253

  • loss and cost

image-20230206152614745

  • fit

image-20230206152955520

模型构造及loss观测

例：

model = Sequential()
model.add(LSTM(50, return_sequences=True,input_shape = (span,1)))
# model.add(LSTM(50))
model.add(Dropout(0.2))
model.add(Dense(1))
model.compile(loss = "mse",optimizer= "adam")
train_history =model.fit(trainX, trainY, epochs= 100, batch_size=50, validation_data=(testX, testY), verbose=1, shuffle=False)

# 画图
plt.figure()
plt.plot(train_history.history["loss"], label = "loss")
plt.plot(train_history.history["val_loss"], label = "val_loss")
plt.legend()
plt.show()

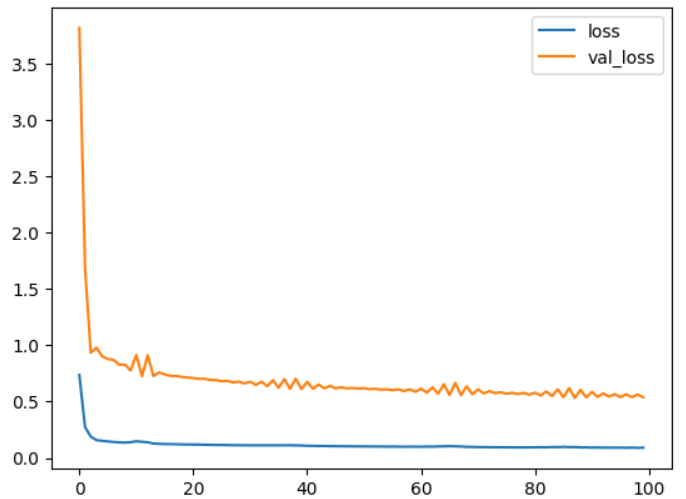
image-20230211143943322

查看模型详情

model.summary()

image-20230211171516861

sklearn

标准化处理

from sklearn.preprocessing import StandardScaler
# 标准化处理
scaler = StandardScaler()
df_for_training_scaled=scaler.fit_transform(df_for_training)

# 反标准化
scaler.inverse_transform(df_for_training)

归一化处理MinMaxScaler

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0,1))
df_for_training_scaled=scaler.fit_transform(df_for_training)
df_for_testing_scaled=scaler.transform(df_for_testing)
df_for_training_scaled

两个特征值 结果为：

image-20230206131827578

GridSearchCV

参考博客

强烈推荐视频

例子

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM
from tensorflow.keras.layers import Dense, Dropout
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import GridSearchCV
def build_model(optimizer):
    grid_model = Sequential()
    # 层数过少导致的问题就是预测的曲线会比较平滑
    grid_model.add(LSTM(60,return_sequences=True,input_shape=(span,1)))
    grid_model.add(LSTM(60))
    # grid_model.add(Dense(64,activation="relu"))
    # Dropout设置防止过拟合的参数,相当于正则化参数
    grid_model.add(Dropout(0.2))
    grid_model.add(Dense(1))
    # 用均方差(mse)作为loss函数
    grid_model.compile(loss = 'mse',optimizer = optimizer)
    return grid_model
# verbose=1设置打印的等级
grid_model = KerasRegressor(build_fn=build_model,verbose=1,validation_data=(testX,testY))
parameters = {'batch_size' : [5],
              # epochs为迭代次数
              'epochs' : [20],
              'optimizer' : ['adam'] }

grid_search  = GridSearchCV(estimator = grid_model,
                            param_grid = parameters,
                            # cv默认值是5折交叉验证
                           )

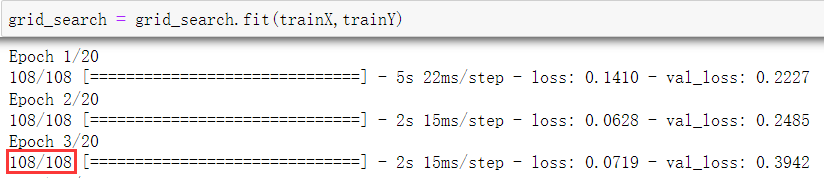
image-20230211105650434

训练集样本数量是675
每一轮的训练次数 = 108 = 675 × ( c v − 1 = 4 c v = 5 ) b a t c h _ s i z e = 5 每一轮的训练次数=108=\frac{675\times(\frac{cv-1=4}{cv=5})}{batch\_size=5} 每一轮的训练次数=108=batch_size=5675×(cv=5cv−1=4​)​

CV交叉验证参数

会将训练集分成CV份,其中 C V − 1 C V \frac{CV-1}{CV} CVCV−1​份用来训练， 1 C V \frac{1}{CV} CV1​用来验证(注意不是测试！！！)

eg:10折交叉验证

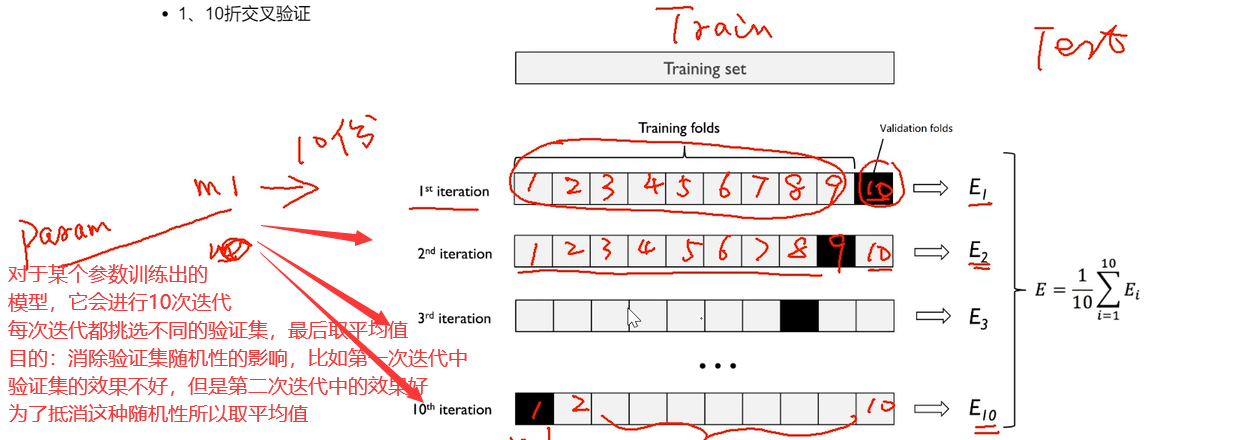
image-20230211114905016

batch_size

会将CV之后的训练集在进行划分，每一份batch_size个

分数

print('Best: {} using {}'.format(grid_search.best_score_, grid_search.best_params_))

最终的分数是在CV交叉验证时针对验证集的拟合情况

所以GridCV中分数高，只代表它在交叉验证环节的分数高，针对的是验证集，但是如果将模型应用到测试集上时，结果并不一定是最好的

image-20230211121118570

batch_size和epoch

一般来说，在合理的范围之内，越大的 batch size 使下降方向越准确，震荡越小

batch取太大会陷入局部最小值，

batch取太小loss会抖动厉害，因为过度关注了每一个数据（包括噪音），所以容易导致过拟合而不是欠拟合

batch_size：一次训练所选取的样本数; batch_size的大小影响内存的使用情况，同时也影响模型的优化程度和速度。

mongoDB

python + mongoDB

import json
# 连接MongoDB数据库
from pymongo import MongoClient
#连接Mongodb数据库
conn = MongoClient('192.168.10.1',27017)

def df2bson(df):
    """DataFrame类型转化为Bson类型"""
    data = json.loads(df.T.to_json()).values()
    return data

# df_data为要存储的数据  table为数据库中表的名称
def saveMongo(df_data,table):
    # userdata为数据库名称
    db = conn["userdata"]
    table = db[table]
    bson_data = df2bson(df_data)
    result = table.insert_many(bson_data)
# 将数据保存到mongodb中
saveMongo(raise_df,"user_raise")

时间戳转日期

https://blog.csdn.net/qq_45366447/article/details/128617142

db.daily_consume.aggregate([
    {
        $project: {
            "Order_time_formatted": {
                $dateToString: {
                    format: '%Y-%m-%d',
                    date: {
                        $add: [
                            ISODate('1970-01-01T00:00:00.000Z'),
                            '$Order_time',
                            28800000
                        ]
                    }
                }
            },
            "_id": "$_id"
        }
    }
]).forEach(function(doc) {
  db.daily_consume.update({
    "_id": doc._id
  }, {
    "$set": {
      "Order_time_formatted": doc.Order_time_formatted
    }
  });
});

在终端中输入上述命令，可以看到已经成功转变过来

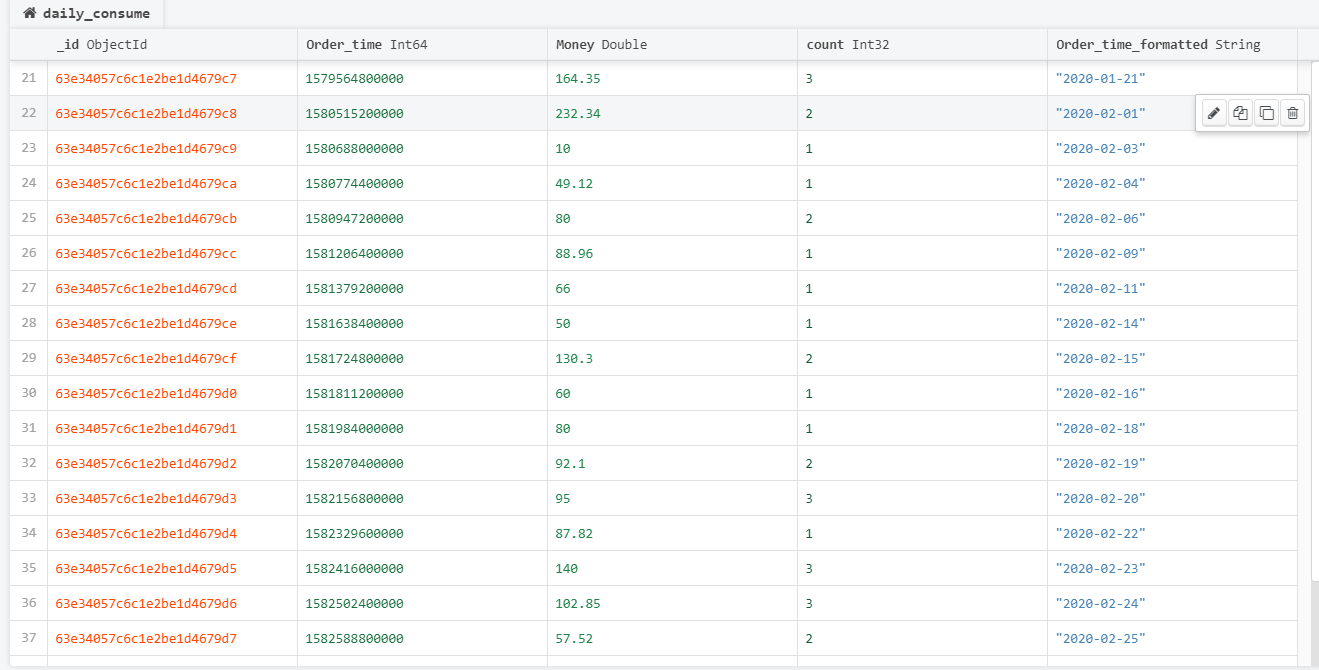
image-20230208152906155

regate([
{
$project: {
“Order_time_formatted”: {
$dateToString: {
format: ‘%Y-%m-%d’,
date: {
a d d : [ I S O D a t e ( ′ 1970 − 01 − 01 T 00 : 00 : 00.000 Z ′ ) , ′ add: [ ISODate('1970-01-01T00:00:00.000Z'), ' add:[ISODate(′1970−01−01T00:00:00.000Z′),′Order_time’,
28800000
]
}
}
},
“_id”: “KaTeX parse error: Expected 'EOF', got '}' at position 14: _id" }̲ } ]).forEa…set”: {
“Order_time_formatted”: doc.Order_time_formatted
}
});
});


在终端中输入上述命令，可以看到已经成功转变过来

[外链图片转存中...(img-mUQrzypv-1696143131169)]

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1055047.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

多线程案例 - 单例模式

多线程案例 - 单例模式

单例模式 ~~ 单例模式是常见的设计模式之一 什么是设计模式 你知道象棋,五子棋,围棋吗?如果,你想下好围棋,你就不得不了解一个东西,”棋谱”,设计模式好比围棋中的 “棋谱”. 在棋谱里面,大佬们,把一些常见的对局场景,都给推演出来了,照着棋谱来下棋,基本上棋力就不会差到哪…
阅读更多...
面试必考精华版Leetcode437. 路径总和 III

面试必考精华版Leetcode437. 路径总和 III

题目&#xff1a; 代码&#xff08;首刷看解析&#xff0c;暴力法&#xff09;&#xff1a; class Solution { public:long rootSum(TreeNode* root,long targetSum){if(!root) return 0;long res0;if(root->valtargetSum){res;} resrootSum(root->left,targetSum-root-…
阅读更多...
2022年9月及10月

2022年9月及10月

9月 1.Halcon12的HObject和Hobject halcon12 可以用HObject&#xff0c;也可以用Hobject&#xff0c;用法都一样 包括HalconCpp.h 如果附加目录中&#xff1a; C:\Program Files\MVTec\HALCON-12.0\include\halconcpp\ 在前面&#xff0c;则用 HalconCpp::HObject 如果附加目录…
阅读更多...
【论文阅读】DiffusionDet: Diffusion Model for Object Detection

【论文阅读】DiffusionDet: Diffusion Model for Object Detection

原文链接&#xff1a;https://arxiv.org/abs/2211.09788 1. 引言 过去的目标检测方法依赖手工设计的候选对象&#xff08;如滑动窗口、区域提案、锚框和参考点&#xff09;&#xff1b;或是依赖可学习的物体查询。   本文使用更加简单的方法&#xff0c;随机初始化边界框&am…
阅读更多...
防火墙基础之H3C防火墙和三层交换机链路聚合的配置

防火墙基础之H3C防火墙和三层交换机链路聚合的配置

H3C防火墙和三层交换机链路聚合的配置 原理概述&#xff1a; 防火墙&#xff08;英语&#xff1a;Firewall&#xff09;技术是通过有机结合各类用于安全管理​与筛选的软件和硬件​设备&#xff0c;帮助计算机网络于其内、外网之间构建一道相对隔绝的保护屏障&#xff0c;以保…
阅读更多...
Docker从认识到实践再到底层原理（七）｜Docker存储卷

Docker从认识到实践再到底层原理（七）｜Docker存储卷

前言 那么这里博主先安利一些干货满满的专栏了&#xff01; 首先是博主的高质量博客的汇总&#xff0c;这个专栏里面的博客&#xff0c;都是博主最最用心写的一部分&#xff0c;干货满满&#xff0c;希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…
阅读更多...
如何让你网站统计的更加精准？

如何让你网站统计的更加精准？

引言 最近对比了自己网站在Cloudflare Analytics和51.la统计的数据&#xff0c;结果发现数值差距的比较大&#xff0c;这是为什么&#xff1f; 经过了摸索&#xff0c;发现了以下几个情况&#xff1a; 广告插件的拦截&#xff0c;大部分广告插件都会拦截网站统计&#xff0c…
阅读更多...
select实现服务器并发

select实现服务器并发

select的TCP服务器代码 #include <stdio.h> #include <unistd.h> #include <string.h> #include <sys/types.h> #include <sys/socket.h> #include <arpa/inet.h> #include <netinet/in.h> #include <sys/select.h> #include…
阅读更多...
【教学类-36-10】20230908方脸爷爷和圆脸奶奶（midjounery-niji）（中班：《我爱我家》数：连线、涂色）

【教学类-36-10】20230908方脸爷爷和圆脸奶奶（midjounery-niji）（中班：《我爱我家》数：连线、涂色）

背景需求&#xff1a; 领导们鼓动我去参加上海市高级职称评审&#xff08;科研成果比较多&#xff09;&#xff0c;为下一轮保教主任评高级“探探路”。虽然自我感觉道行浅薄&#xff0c;无缘高级&#xff0c;但领导给机会&#xff0c;自然要参与一下&#xff0c;努力了解整个…
阅读更多...
10.1select并发服务器以及客户端

10.1select并发服务器以及客户端

服务器&#xff1a; #include<myhead.h>//do-while只是为了不让花括号单独存在&#xff0c;并不循环 #define ERR_MSG(msg) do{\fprintf(stderr,"%d:",__LINE__);\perror(msg);\ }while(0);#define PORT 8888//端口号1024-49151 #define IP "192.168.2.5…
阅读更多...
10月1日作业

10月1日作业

汇编指令合集 用select实现服务器并发代码 #include<myhead.h> #define IP "192.168.0.106" #define PORT 8888int main(int argc, const char *argv[]) {//新建套接字文件int sfd socket(AF_INET, SOCK_STREAM, 0);if(sfd < 0){ERR_MSG("socket&quo…
阅读更多...
imgui开发笔记＜4＞、image-slider online

imgui开发笔记＜4＞、image-slider online

在线滑条二值化。 // // Created by sry on 2021/6/30. //#include"imgui.h" #include "imgui_impl_glfw.h" #include "imgui_impl_opengl3.h" #include <stdio.h> // Initialize with gl3wInit() #include<GL/gl3w.h> // Include …
阅读更多...
【MATLAB第78期】基于MATLAB的VMD-SSA-LSTM麻雀算法优化LSTM时间序列预测模型

【MATLAB第78期】基于MATLAB的VMD-SSA-LSTM麻雀算法优化LSTM时间序列预测模型

【MATLAB第78期】基于MATLAB的VMD-SSA-LSTM麻雀算法优化LSTM时间序列预测模型 一、LSTM data xlsread(数据集.xlsx);% [x,y]data_process(data,15);%前15个时刻 预测下一个时刻 %归一化 [xs,mappingx]mapminmax(x,0,1);xxs; [ys,mappingy]mapminmax(y,0,1);yys; %划分数据 n…
阅读更多...
Android进阶——Handler底层fd监听之epoll机制

Android进阶——Handler底层fd监听之epoll机制

文章大纲 引言一、从网卡接收数据说起二、如何知道接收了数据&#xff1f;三、进程阻塞为什么不占用cpu资源&#xff1f;四、那么阻塞的原理是什么&#xff1f;1、工作队列2、等待队列3、唤醒进程 五、内核接收网络数据全过程六、同时监视多个socket的简单方法七、epoll的设计思…
阅读更多...
Redis入门到精通——00数据类型

Redis入门到精通——00数据类型

1、String 1.1、介绍 String 是最基本的 key-value 结构&#xff0c;key 是唯一标识&#xff0c;value 是具体的值&#xff0c;value其实不仅是字符串&#xff0c; 也可以是数字&#xff08;整数或浮点数&#xff09;&#xff0c;value 最多可以容纳的数据长度是 512M 1.2、…
阅读更多...
聊天、会议、多媒体一体化：多平台支持的即时通讯系统 | 开源日报 No.44

聊天、会议、多媒体一体化：多平台支持的即时通讯系统 | 开源日报 No.44

harness/gitness Stars: 28.2k License: Apache-2.0 Gitness 是一个建立在 Drone 之上的新型开源开发者平台&#xff0c;具备代码托管和流水线功能。它提供了以下核心优势&#xff1a; 轻量级、超快速的代码托管和持续集成服务支持 Docker 容器化部署可以在本地环境中构建和…
阅读更多...
【C/C++笔试练习】二维数组、二维数组的访问，解引用，地址计算、计算糖果、进制转换

【C/C++笔试练习】二维数组、二维数组的访问，解引用，地址计算、计算糖果、进制转换

文章目录 C/C笔试练习1.二维数组&#xff08;1&#xff09;二维数组的访问&#xff08;2&#xff09;二维数组的初始化&#xff08;3&#xff09;二维数组的解引用&#xff08;4&#xff09;二维数组的解引用&#xff08;5&#xff09;多维数组的解引用&#xff08;6&#xff0…
阅读更多...
没有社会性的人机环境系统智能是危险的

没有社会性的人机环境系统智能是危险的

缺乏社会性的人工智能常常存在着一定的潜在危险性&#xff0c;这是因为&#xff1a; 首先&#xff0c;社会性对于人类而言是非常重要的&#xff0c;我们通过社交互动、合作和沟通来建立联系、理解他人以及共同解决问题。人类具有复杂的情感和道德价值观&#xff0c;这些因素在我…
阅读更多...
嵌入式学习笔记（39）蜂鸣器和PWM定时器编程实践

嵌入式学习笔记（39）蜂鸣器和PWM定时器编程实践

7.4.1蜂鸣器的工作原理 (1)蜂鸣器里边有2个金属片&#xff0c;离得很近但没挨着。没电的时候两个金属片在弹簧本身的张力作用下分开彼此平行&#xff0c;有电的时候两边分别充电&#xff0c;在异性电荷的吸力作用下两个片挨着。 (2)我们只要以快速的频率给蜂鸣器的正负极供电…
阅读更多...
redis使用学习笔记

redis使用学习笔记

文章目录 关于redis的简单性能概括Redis命令行客户端Redis命令Redis通用命令String类型key的层级格式Hash类型List类型Set类型SortedSet类型 Redis的Java客户端Jedis使用基本步骤Jedis连接池 SpringDataRedisRedisTemplate快速入门RedisSerializer 关于redis的简单性能概括 键…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023