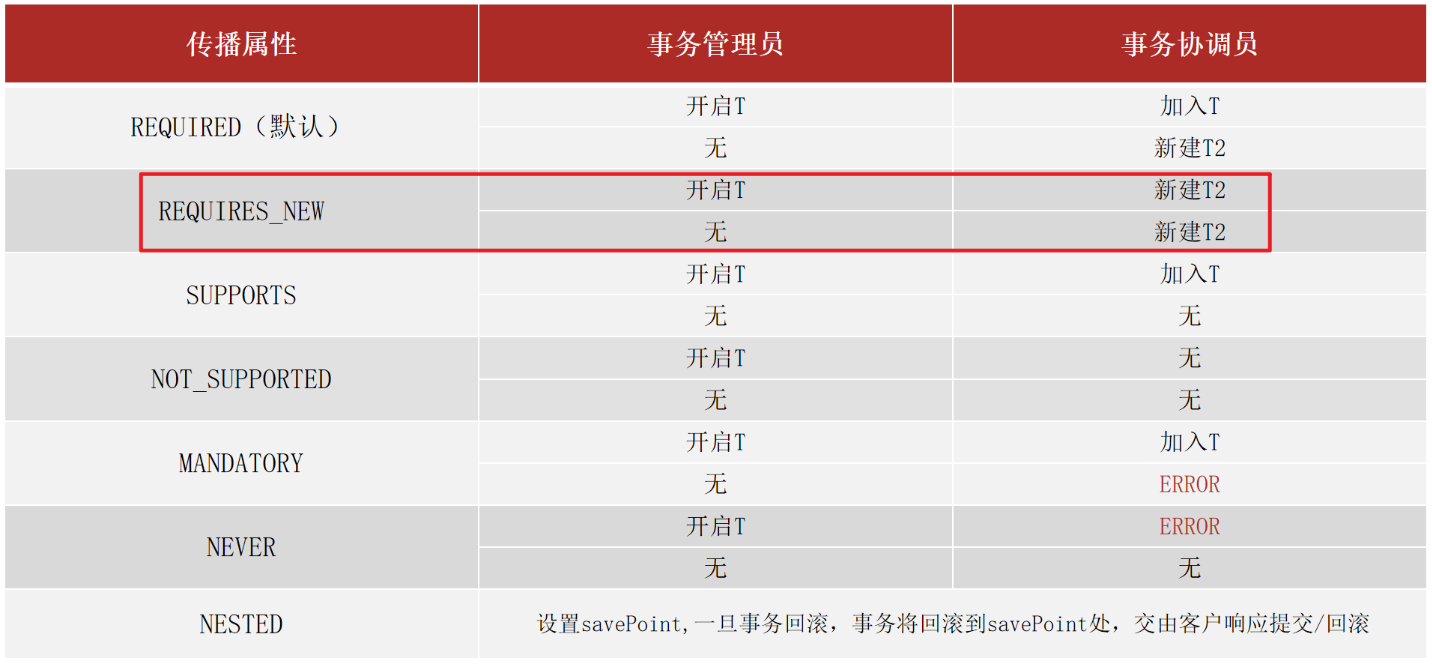
正态分布(高斯分布)
若随机变数
X
X
X 服从一个期望
μ
\mu
μ,标准差 的正态分布
σ
\sigma
σ,则记为
X
≈
N
(
μ
,
σ
2
)
X \approx N(\mu,\sigma^2)
X≈N(μ,σ2),其密度函数为:
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
2
σ
2
f(x) = \frac 1{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
f(x)=σ2π1e−2σ2(x−μ)2
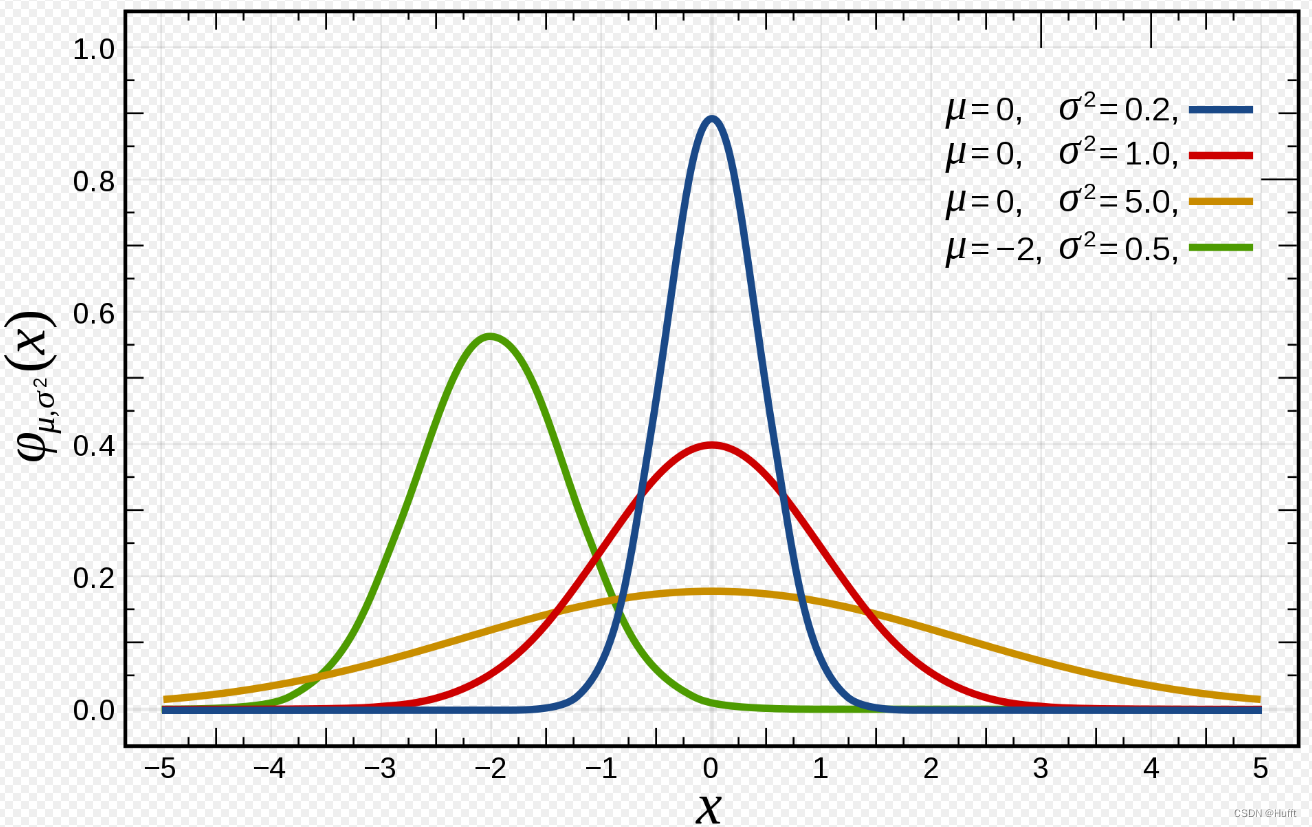
其具有以下性质:
- μ \mu μ 期望(平均值),图像关于 x = μ x = \mu x=μ 对称
- 图像在 x = μ x = \mu x=μ 处达到峰值 1 σ 2 π \frac 1{\sigma \sqrt{2\pi}} σ2π1
- 曲线与 x x x 围成的面积是 1
- σ \sigma σ 标准差表示数据离散的程度,由于围成的面积固定,当 μ \mu μ 一定时, σ \sigma σ 越大图像越矮胖, σ \sigma σ 越小图像越高瘦
- μ = 0 \mu = 0 μ=0, σ = 1 \sigma = 1 σ=1 时为标准正态分布
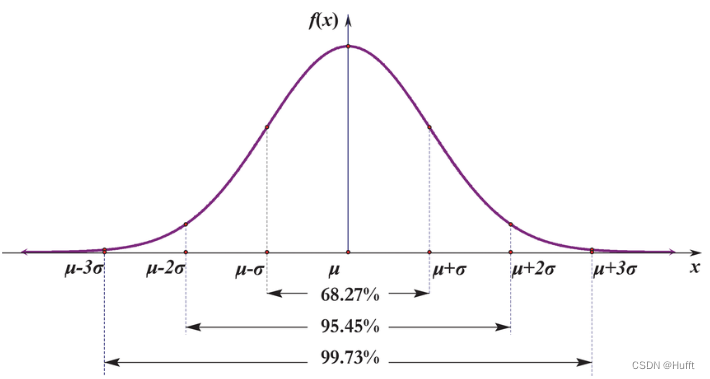
-
3
σ
3\sigma
3σ原则:



![[python 刷题] 刷题常用函数](https://img-blog.csdnimg.cn/7583d0f7c50943988bf15d9726ce6178.png)