📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

目录
前言
1. 快速排序
1.1 hoare版本
1.2 挖坑法
1.3 双指针版本
2. 非递归实现快速排序
总结
前言
快速排序是一种常用的排序算法,也是一种很高效的排序的,它是由Hoare于1962年提出的一种二叉树结构的交换排序方法。本篇文章我将带你深入了解快速排序。
1. 快速排序
快速排序是一种常用的排序算法,它的基本思想是通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列的目的。快速排序常见的实现方法主要分为三种版本:
- hoare版本
- 挖坑法版本
- 前后指针版本
我们废话不多说直接步入正题。
1.1 hoare版本
hoare版本是选择一个key值(一般选用最左边)例如:

然后开始从数组两边开始移动寻找符合条件的值,R向左移动寻找小于key的值,L向右移动寻找大于key的值。R和L都找到符合条件的数字后进行交换。

然后再继续走,直到L和R相遇停止。
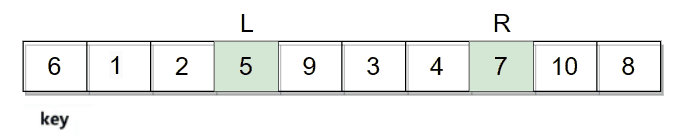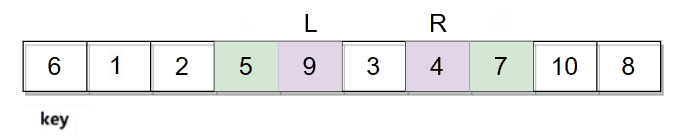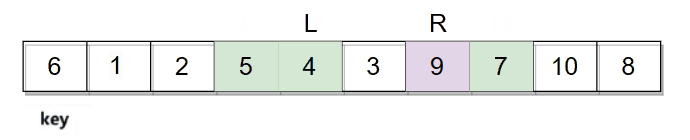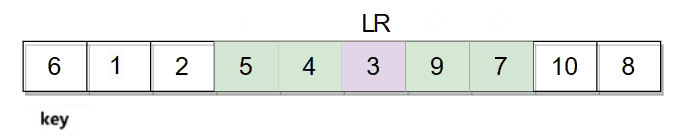
它们相遇的位置是数字3,3比key小,最后再将相遇位置的数据和key的数据进行交换。整个逻辑过程如下图:
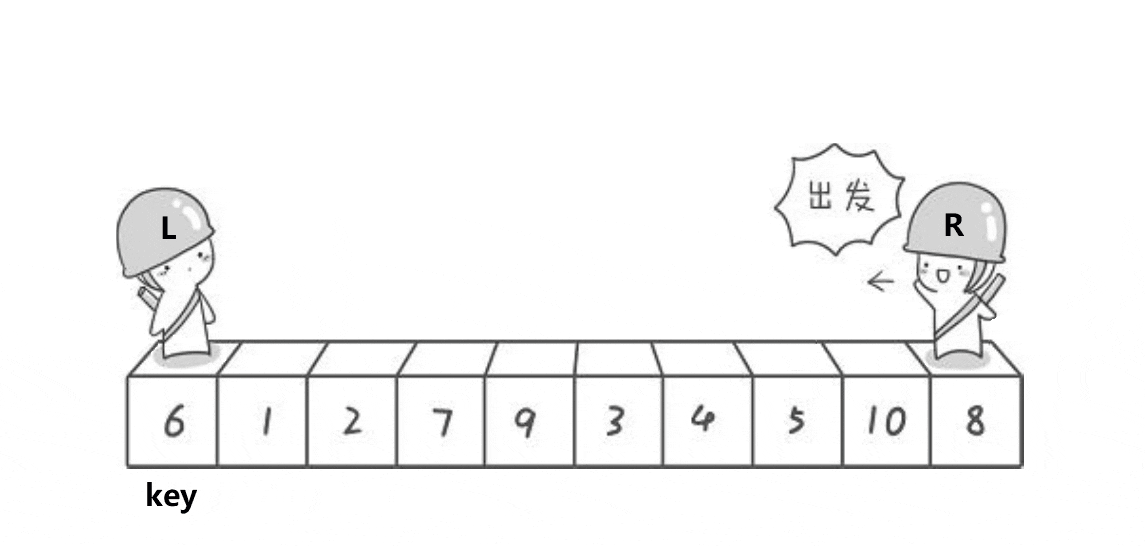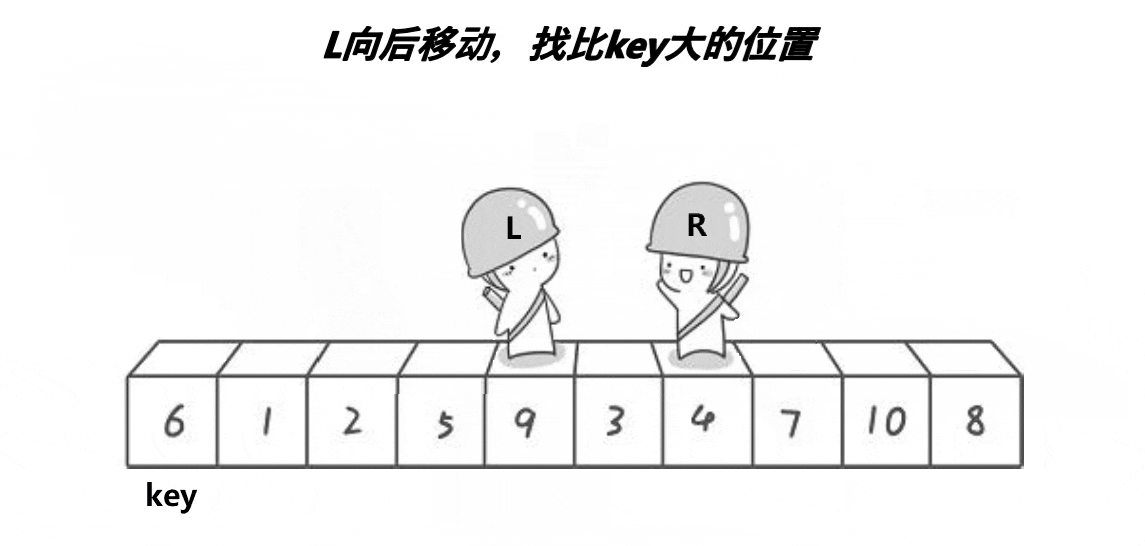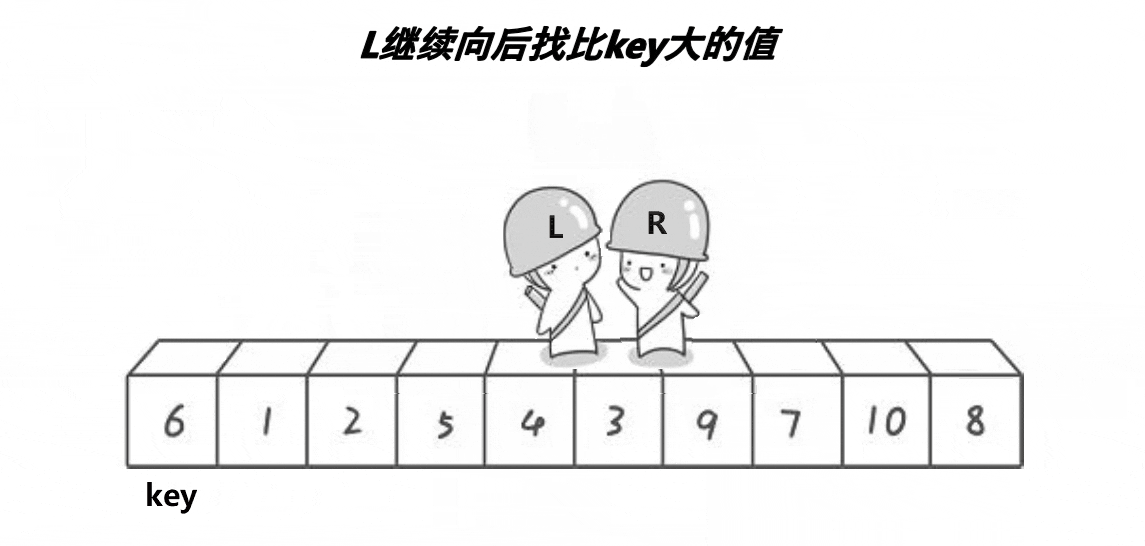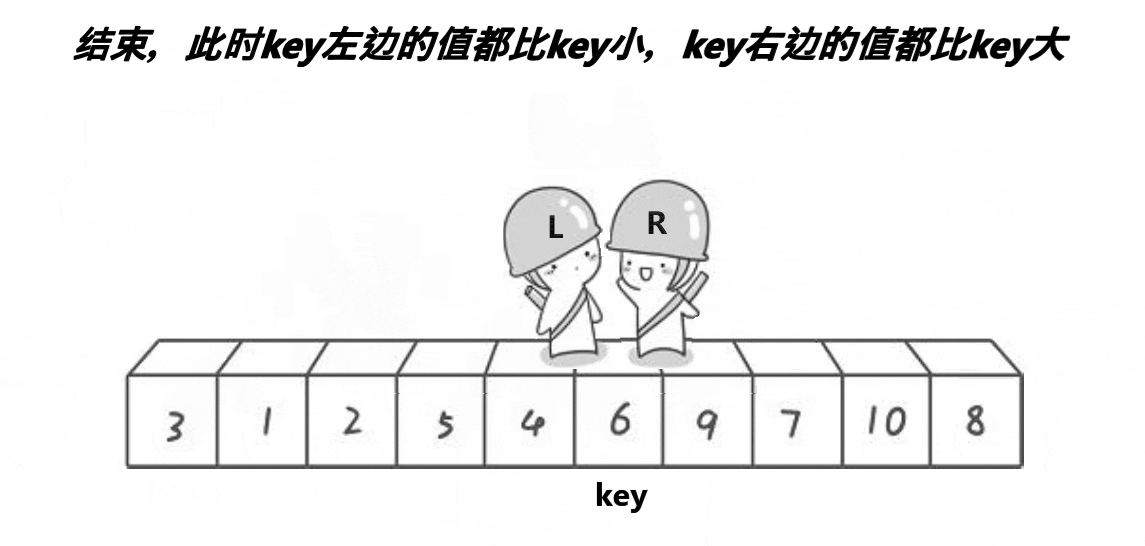
这个图呈现的逻辑过程更加形象,然后我们再从R和L相遇的位置将数组分为两部分,当左半部分和右半部分有序,那么这个数组就会有序,所以我们重复上述过程:

继续分,数组最终被细分为一个数据或没有数据。
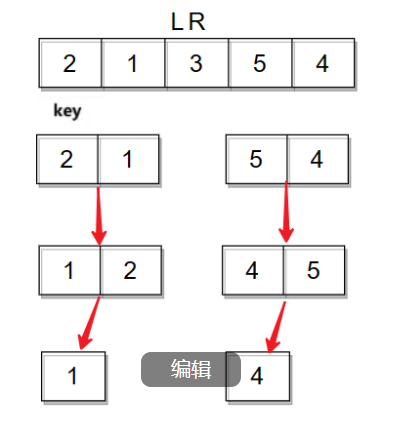
当数据为1个或没有时就开始返回,执行完毕后左半部分就变得有序,右半部分也是这样的逻辑,返回后两边子数组就会变得有序,进而使整个数组有序。以上便是hoare版本的整个过程。
接下来我们对代码进行实现:
void PathSort(int* a, int left,int right)
{
int key = a[left];
while (left < right)
{
while (a[right] > a[key])
{
right--;
}
while (a[left] < a[key])
{
left--;
}
Swap(&a[left], &a[right]);
}
Swap(&key, &a[right]);
}快速排序的hoare版本有很多的坑,上述的代码是否存在错误呢?
上述的代码存3个问题:
- 死循环问题
- 数组越界问题
- key值交换问题
首先是死循环问题,R要找比key小的数据,L要找比key大的数据,那当L和R都遇到了和key相同的数据时,它们都停止移动,开始进行交换,交换后仍然相等,以此往复一直交换,进而形成了死循环。
数组越界问题,R找比key的值,如果R一直到数组遍历结束都没有找到,那它就会发生越界。
key值交换问题,我们在上述逻辑中,需要将key值(第一个数据)位置上的数据与L和R相遇位置的数据进行交换。而上述代码中交换的是key的值与L和R相遇位置的数据,实际上第一个数据(key值位置)并没有变,这样会造成数据丢失。
这三个问题都是在编写代码时经常遇到的错误。改正后代码如下:
int PathSort(int* a, int left,int right)
{
int key = left;
while (left < right)
{
while (right>left && a[right] >= a[key])
{
right--;
}
while (right > left && a[left] <= a[key])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}
上述代码我们是进行了一次调整,接下来就是递归使得左右两边数组有序。递归调用这里没有什么问题,重点在于递归结束条件。当递归到最后时,要么是数组只有一个数据,要么是没有数据。
那要如何编写设置结束条件呢?
以左边递归为例:第一次进入左边区间是0到4,第二次是0到1,然后key是下标为1的数据,key-1=0,第三次调用传入的key-1=begin=0,返回后调用右边,右边没有数据,key+1=2,end=1,所以由此我们可以做出判断,当begin>=end时,就证明递归已经到最小,然后就返回。
递归过程如下图:

void QuickSort(int* a, int begin,int end)
{
if (begin >= end)
{
return;
}
int key=PathSort(a, begin, end);
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}从上述的逻辑过程,可以发现L和R相遇的位置一定比key小(相遇位置比key小交换才有意义),那凭什么说L和R相遇位置一定比key小?
它是有一个前提的,就是一定要让R先走,但是又会存在两种情况:
- 最后一次R不动让L去相遇。
- L不动让R去相遇。
如下图让R先走,最后是R不动让L去相遇,但如果是L先走,当R到下标为6的位置停止交换后,L开始走,此时相遇位置就会变成下标为6的位置,数据是9比6大。(R不动,让L去相遇)
当然还有一种情况,最后一次时是L不动让R去相遇:

两次交换后如上图,此时R先走,11比key大R会继续走,R就会去和L相遇,相遇的位置还是比key小(L和R交换后,L位置数据一定比key小)。
上述的方式和代码排序很不稳,上述过程最理想的状态是key的值是中位数,这样在分割数组进行递归时能尽可能将数组二分。
最坏的情况就是没有比key小的数据或者大的数据,那么就会造成如下情况:
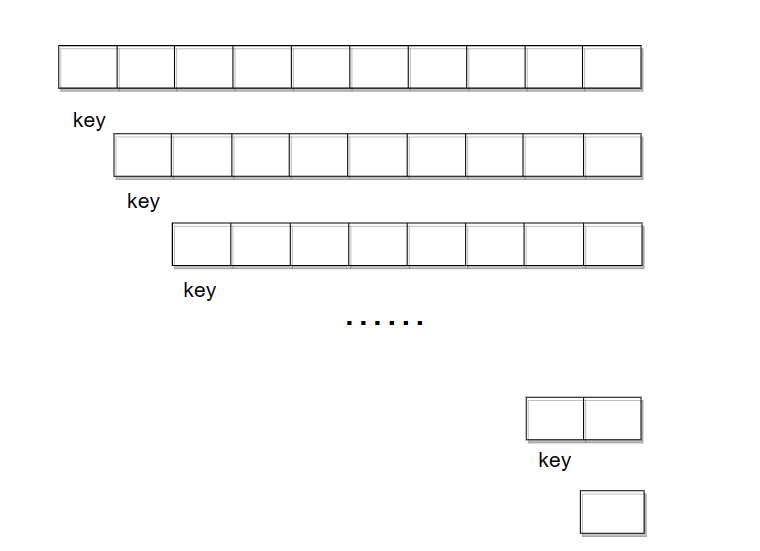
这样它的时间复杂度和空间复杂度也会变差,所以我们还需要对hoare版本的进行优化,以避免这样情况的发生。我们可以将左右和中间的值进行比较,取三数的中间值作为key值。优化后:
//三数取中
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[mid] > a[left])
{
if (a[mid] < a[right])
{
return mid;
}
else if(a[left]>a[right])
{
return left;
}
else
{
return right;
}
}
else//a[left]>a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] < a[left])
{
return right;
}
else
{
return left;
}
}
}
int PathSort(int* a, int left,int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int key = left;
while (left < right)
{
while (right>left && a[right] >= a[key])
{
right--;
}
while (right > left && a[left] <= a[key])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}1.2 挖坑法
挖坑法是对hoare版本思路上的一种优化,挖坑法的整体逻辑如下:
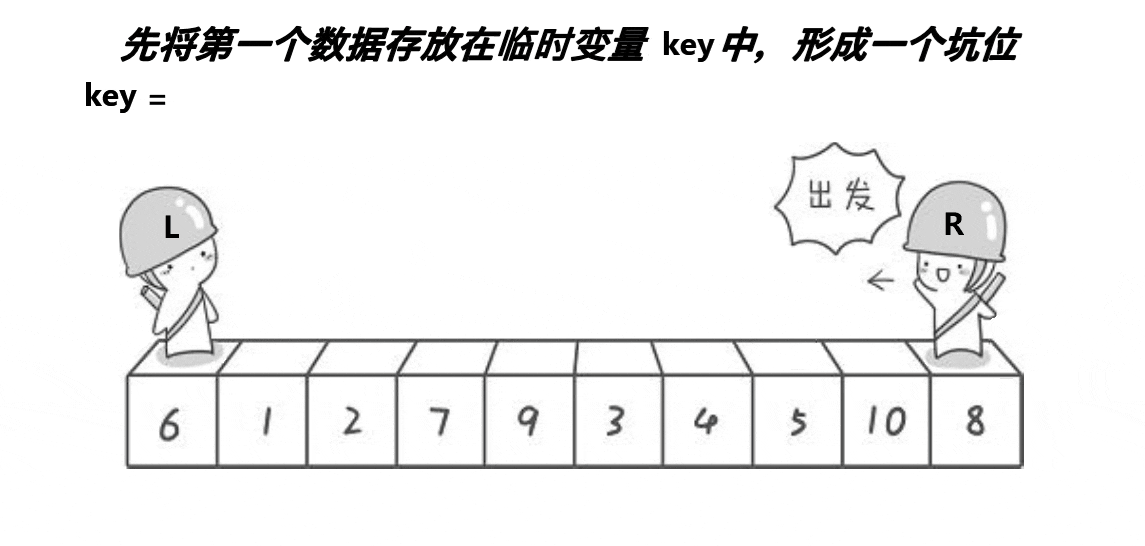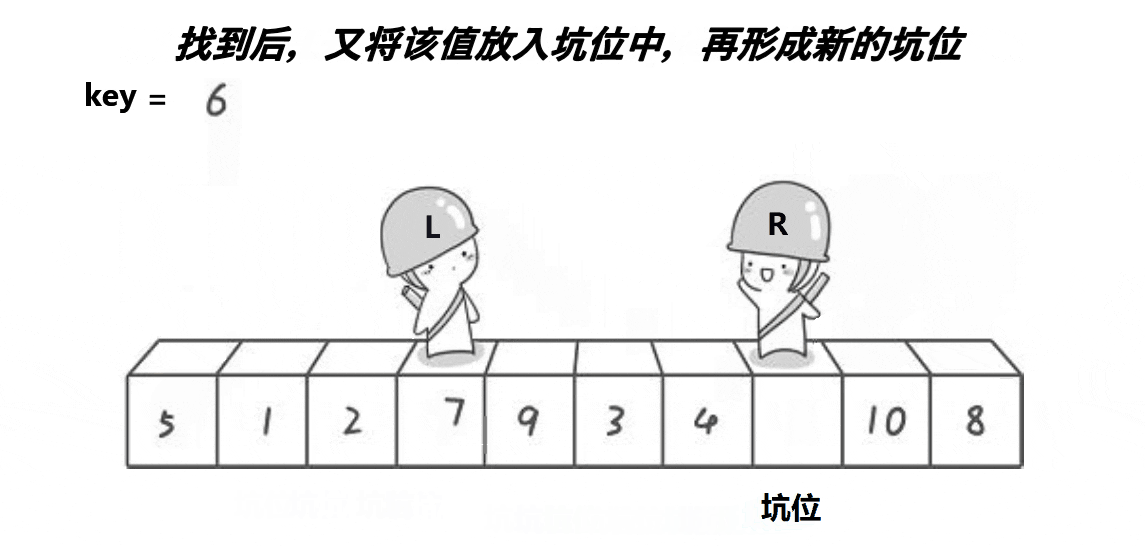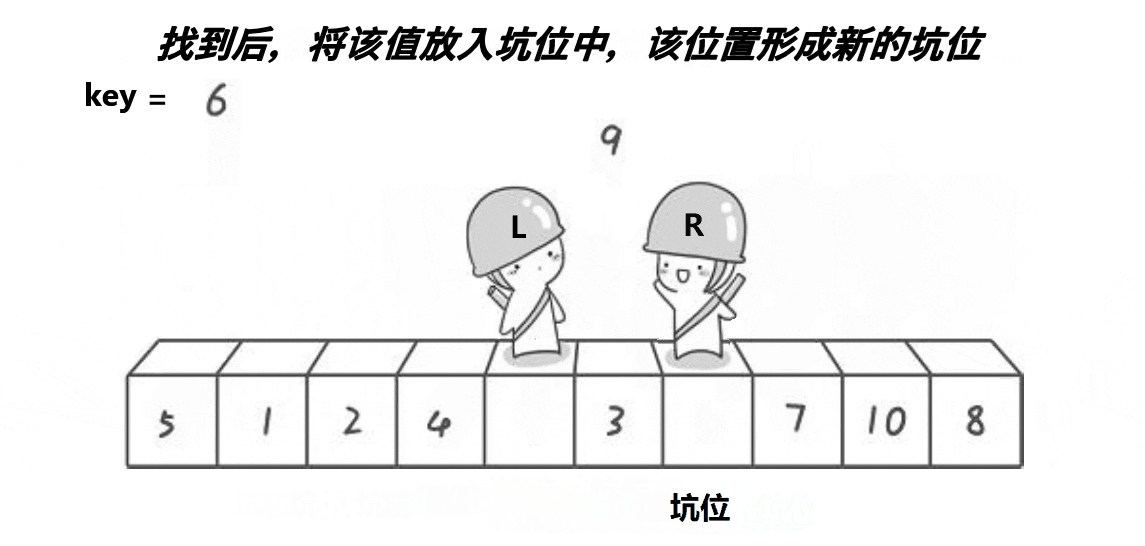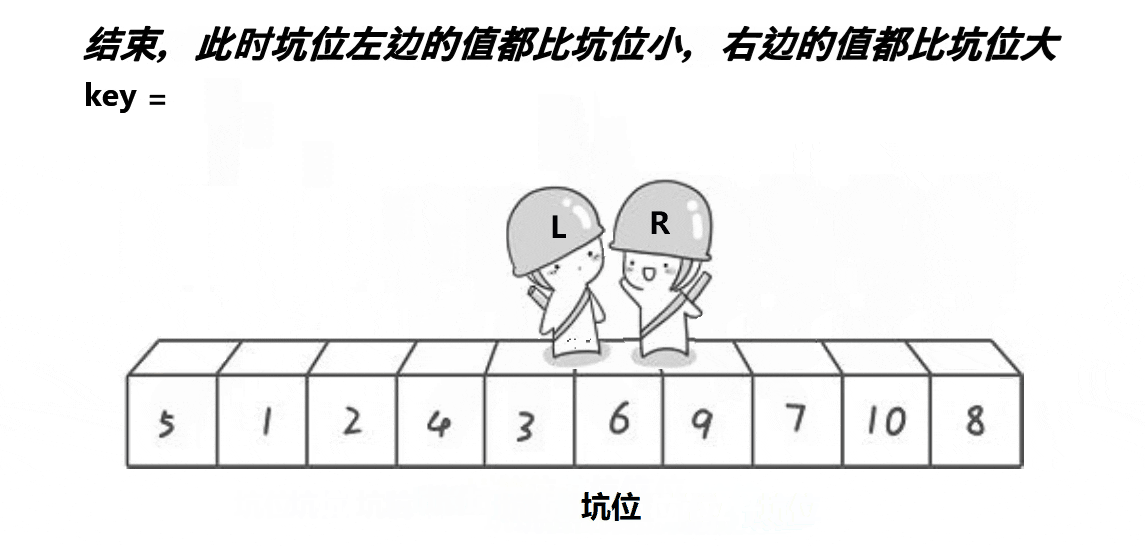
挖坑法不用考虑R先走还是L先走,开始时第一个数据作为坑位,必须R先走,R找到比key小的数数据填补到坑位,R位置形成新的坑位。然后L开始走,遇到比key大的将数据填补到坑位,然后L位置形成新的坑位。具体代码如下:
int PathSort2(int* a, int left, int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int key = a[left];
//保存key值左边形成第一个坑位
int hole = left;
while (left < right)
{
//右边先走,寻找比key小的数据,填补到左边坑位
while (right > left && a[right] >=key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边走,寻找比key大的数据,填补到右边坑位
while (right > left && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] =key;
return hole;
}1.3 双指针版本
双指针法是对快排的更近一步优化,相对于前两种,思路和代码也更简单,使用两个指针cur和prev,来控制数据进行调整。
逻辑如下:
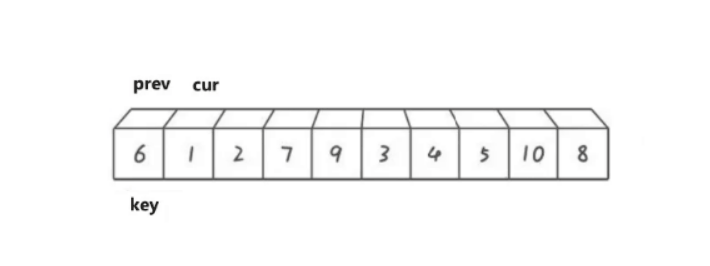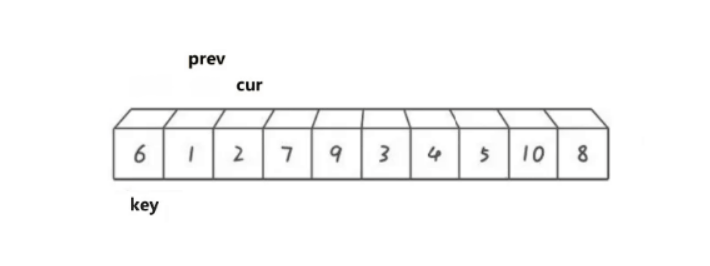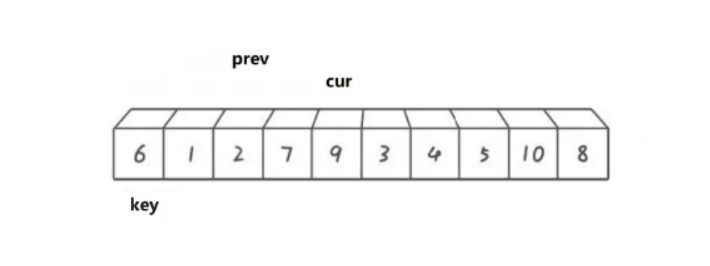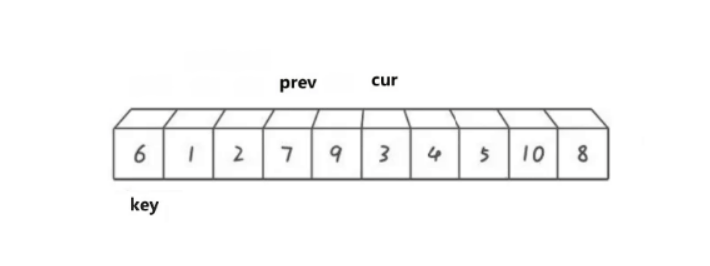
cur遍历数组,如果cur比key小,那就prev向后移动,将prev指向的数据于cur指向的数据进行交换。
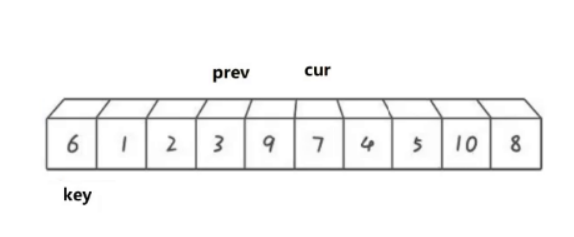
然后cur继续向后走,遇到比key小的数据就重复上述过程:
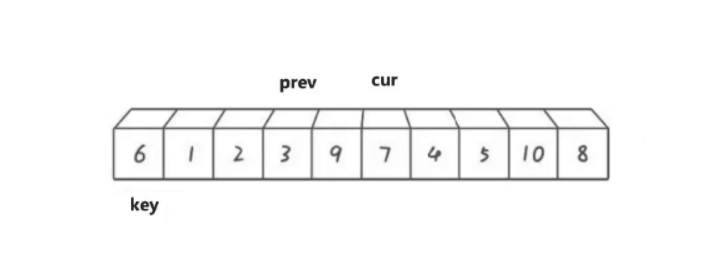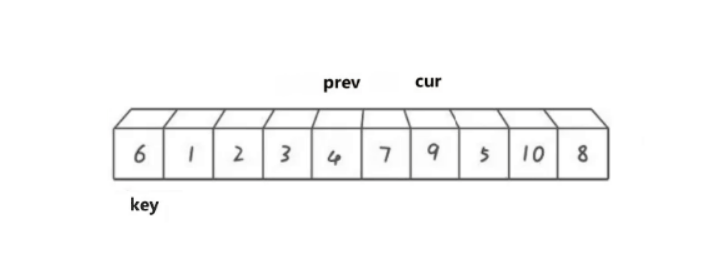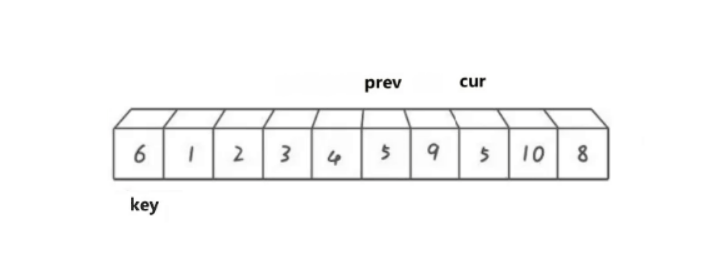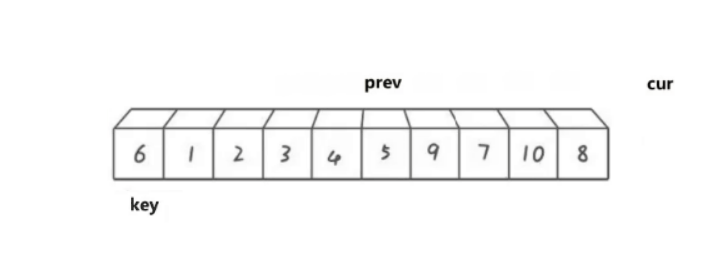
直到cur遍历结束停止,之后再将prev最终指向位置的数据与key位置的数据进行交换。最终情况如下图:
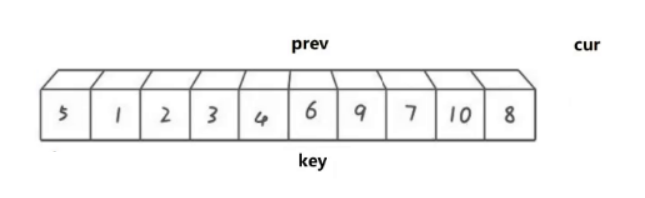
根据上述的逻辑,我们对代码进行实现:
int PathSort3(int* a, int left, int right)
{
int cur = left + 1;
int prev = left;
int key = left;
while (cur <= right)
{
if (a[cur] <a[key] )
{
prev++;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[key], &a[prev]);
return prev;
}在cur指向1和2时,cur指向的数据依然和prev指向的数据进行了交换(此时cur和prev指向同一个数据),此时交换并没有什么意义,所以我们也可以为了防止prev和cur指向同一位置时进行交换,这里我们可以进行优化:
int PathSort3(int* a, int left, int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int cur = left + 1;
int prev = left;
int key = left;
while (cur <= right)
{
if (a[cur] <a[key] && ++prev!=cur)
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[key], &a[prev]);
return prev;
}双指针法不需要考虑从哪边先走,也不需要考虑数组越界问题,代码和逻辑都十分的清晰简单。在这三种方法的实际调用时都是使用了递归,来进行分治排序。
但快速排序使用递归是需要不断进行开空间的,快速排序的二分递归模式类似于满二叉树,我们知道,满二叉树的后两层的节点个数占了总个数的75%,所以我们可以考虑在递归到小区间时使用插入排序来进行优化。
void QuickSort2(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if ((end - begin + 1) > 10)
{
int key = PathSort3(a, begin, end);
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
同时我们还可以使用非递归的方法来实现快排。
2. 非递归实现快速排序
上述的快速排序使用了递归,但使用递归还是存在弊端的,递归的深度问题,递归创建的空间在栈区,而栈区的空间大概只有8MB,所以我们还是很有必要学习非递归的方法。
非递归实现快排需要用到栈的数据结构,通过栈来模拟系统栈区。
不断地入栈每次调整的数组区间,使用栈的特性来模拟递归调用的调整函数。
还是以上述的数组为例:
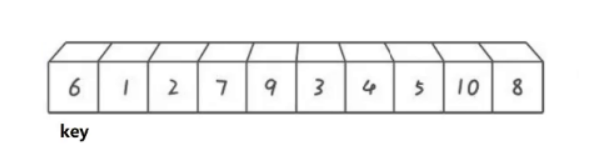
以左边为例:

先入栈0和9(数据的区间下标),然后出栈,取栈顶元素作为调整函数的参数,然后调用调整函数,再将key两边的数组下标区间入栈,直至栈为空结束。具体代码实现如下:
逻辑比较简单,不再进行细节讲解。
void QuickSort3(int* a, int begin, int end)
{
Stack st;
InItStack(&st);
StackPush(&st, end);
StackPush(&st, begin);
while (!IsEmpty(&st))
{
int left=TopData(&st);
StackPop(&st);
int right = TopData(&st);
StackPop(&st);
int key =PathSort3(a, left, right);
if (key < right)
{
StackPush(&st, right);
StackPush(&st, key+1);
}
if (left < key - 1)
{
StackPush(&st, key - 1);
StackPush(&st, left);
}
}
DestoryStack(&st);
}总结
快速排序是一种极其高效的排序方法,从上述的分析快速排序使用的二分分治排序的方法,可以得出时间复杂度为O(N*logN),同时快速排序并不稳定,我们使用了各种方法来进行优化,使它的时间复杂度稳定在O(N*logN)。好了以上便是本期全部内容,感谢阅读!