前言

文章介绍了一种用于视觉信息提取（VIE）的预训练模型：GeoLayoutLM。GeoLayoutLM通过显式建模几何关系和特殊的预训练任务来提高文本和布局的特征表示。该模型能够提高文档信息抽取的性能。

一、提出背景

当前多模态预训练模型在 SER 任务中已取得较好结果，但在 RE 任务中表现仍有待提高。

LayoutLMv3并没有充分利用有用的几何关系信息：

(a) LayoutLMv3 倾向于链接两个实体，它们更依赖于它们的语义，而不是几何布局；

(b) LayoutLMv3 成功地预测了上半部分的链接，但忽略了下面的链接，尽管这两个链接在几何布局上是相似的。

这两个例子说明了几何信息在关系提取（RE）中的重要性。

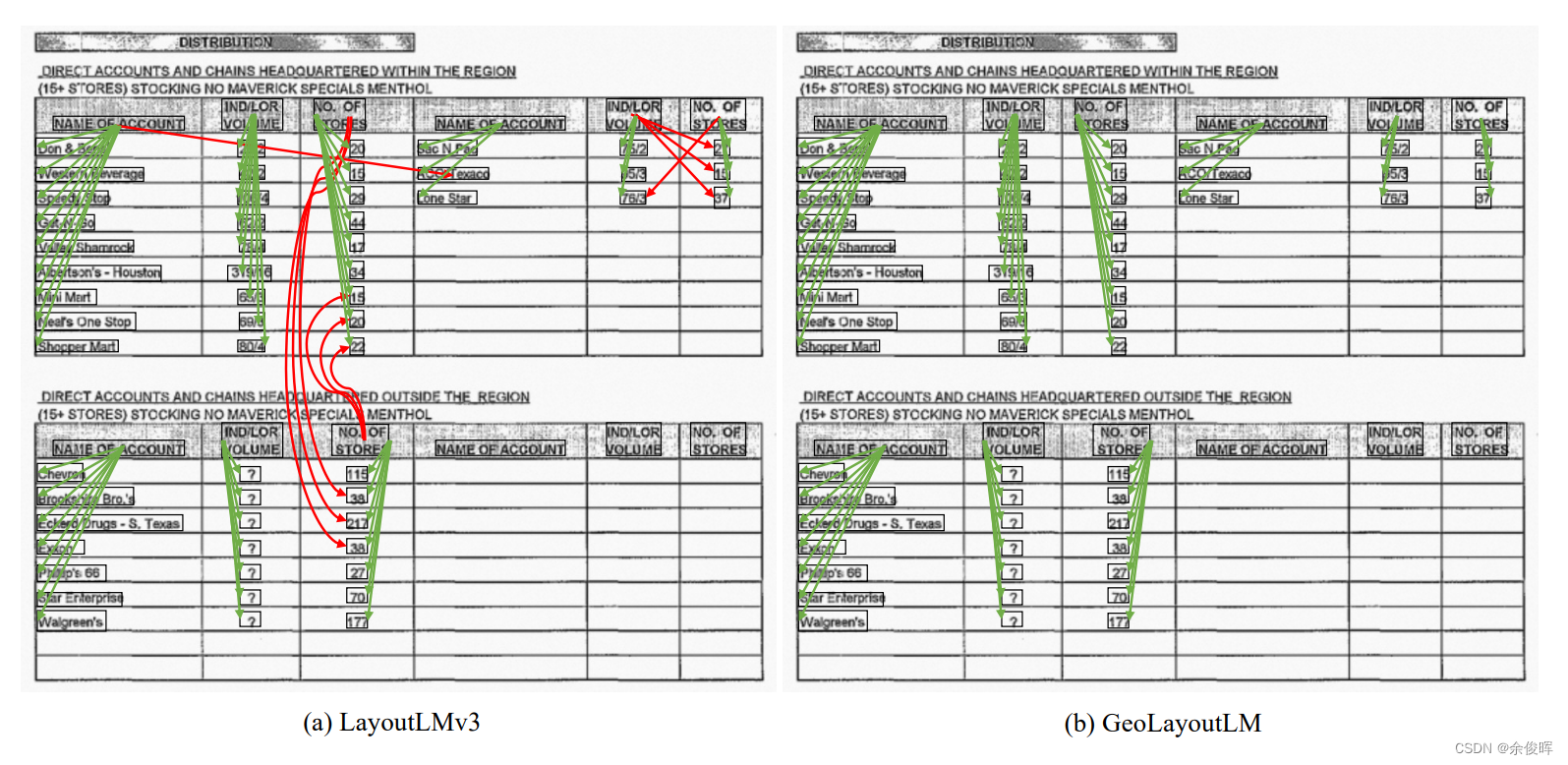
LayoutLMv3通过引入简单的几何限制（在FUNSD数据集上）来提高RE性能：

二、主要贡献

1. 显式建模几何关系：GeoLayoutLM通过显式建模文本和布局之间的几何关系来解决现有预训练模型在处理文档时存在的局限性。这种显式建模可以更好地捕捉文本和布局之间的关联，从而提高文档智能的性能。

2. 特殊的预训练任务：GeoLayoutLM采用了三个特殊的几何相关预训练任务来实现几何预训练，并设计了新的关系头来丰富和增强特征表示。这些预训练任务和关系头有助于GeoLayoutLM更好地处理文档中的几何信息，并提高文本和布局的特征表示。

3. 端到端的模型架构：GeoLayoutLM的模型架构包括一个独立的视觉模块、一个文本布局模块和交互式的视觉和文本协同注意力层，这些都有助于提高文本和布局的特征表示。GeoLayoutLM的端到端模型架构可以更好地处理文档中的多模态信息，并提高文档智能的性能。

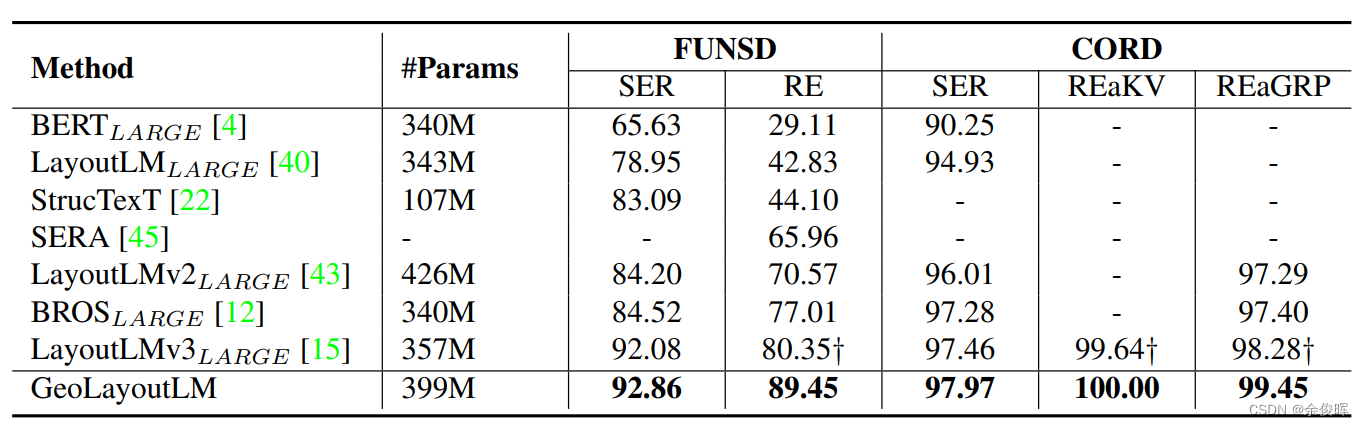
4. 竞争性能表现：GeoLayoutLM在多个标准的VIE基准测试中取得了高竞争性的性能表现，证明了其在文档智能领域的实用性和有效性。

三、模型结构

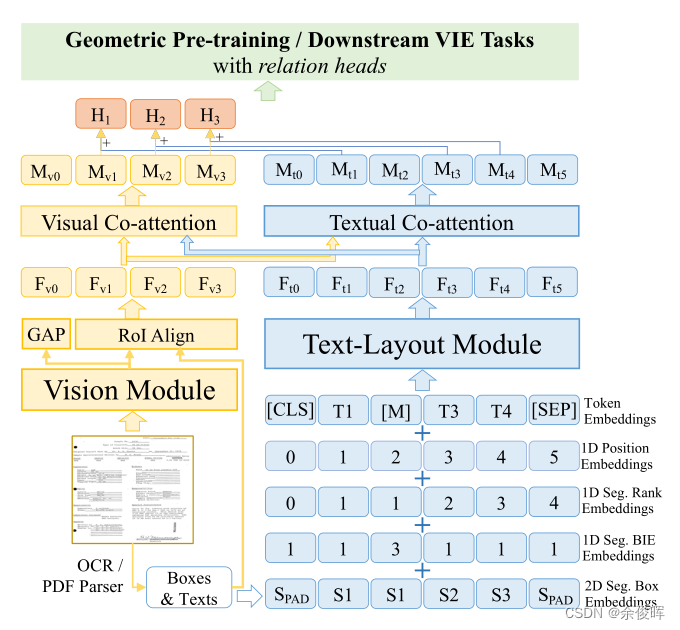
GeoLayoutLM是一个多模态的框架，用于视觉信息提取（VIE）。该结构受双流结构的启发，它的模型结构由三个主要部分组成：独立的视觉模块、文本布局模块和交互式的视觉和文本共同关注层：

1. 视觉模块：视觉模块用于提取文档图像中的视觉特征。GeoLayoutLM使用ConvNeXt和multi-scale FPN作为视觉模块的主干网络，以提取不同尺度的特征。ConvNeXt是一种卷积神经网络结构，它在多个维度上进行卷积操作，可以提高模型的表达能力。multi-scale FPN是一种特征金字塔网络，可以在不同尺度上提取特征，以适应不同大小的文本。
2. 文本布局模块：文本布局模块用于提取文档图像中的文本布局信息。GeoLayoutLM使用BROS作为文本布局模块，它是一种基于区域的文本检测和识别方法。BROS可以检测文本区域，并将其分配到相应的文本行和段落中。
3. 交互式的视觉和文本协同注意力层：交互式的视觉和文本协同注意力层用于将视觉和文本信息融合起来，以提高模型的性能。GeoLayoutLM使用transformer解码器层作为协同注意力层，它可以对视觉和文本信息进行交互式的编码和解码，以提取它们之间的关系。

四、预训练任务

4.1 掩蔽视觉语言模型（MVLM）

为了得到多模态的上下文表示，引入MVLM预训练，可以参考：《LayoutLM: Pre-training of Text and Layout for Document Image Understanding》，损失函数定义为：$L_{MVLM}$

4.2 自监督几何预训练任务

为了更好地用几何信息表示文档布局，引入了三种几何关系：

GeoPair：两个文本段之间的关系

GeoMPair：多个文本段对之间的关系

GeoTriplet：三个文本段之间的关系

并且围绕这三种关系设计了三种预训练任务。

a.Direction and Distance Modeling（DDM）

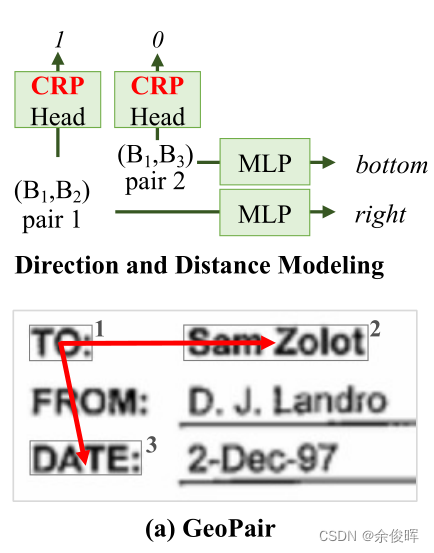
DDM旨在帮助模型理解文档中两个文本片段之间的相对位置关系。 DDM包含两个子任务：方向建模和距离建模。方向建模是一个9个方向的分类问题，模型预测两个文本片段之间的方向概率。这9个方向包括8个相邻方向和1个重叠方向。方向建模使用softmax函数应用于一个线性层，该线性层连接两个文本片段的特征。
$$P_{ij}^{direct}=\mathrm{Softmax}(\mathrm{Linear}([B_i,B_j]))$$
距离建模是一个二分类问题，用于确定第j个文本片段是否在它们的方向上最接近第i个文本片段。两个片段之间的距离定义为它们的边界框之间的最小距离。距离建模使用sigmoid函数应用于一个双线性层，该双线性层以两个文本片段的特征作为输入。
$$P_{ij}^{dist}=\mathrm{Sigmoid}(\mathrm{Bilinear}(B_i,B_j))$$
损失函数：
$${\mathcal{L}}_{DDM}=\mathrm{CrossEntropy}(P^{direct},Y^{direct})+\mathrm{BCELoss}(P^{dist},Y^{dist})$$
小结：通过在DDM上进行预训练，GeoLayoutLM学习了建模文本片段之间的几何关系。

b.Detection of Direction Exceptions（DDE）

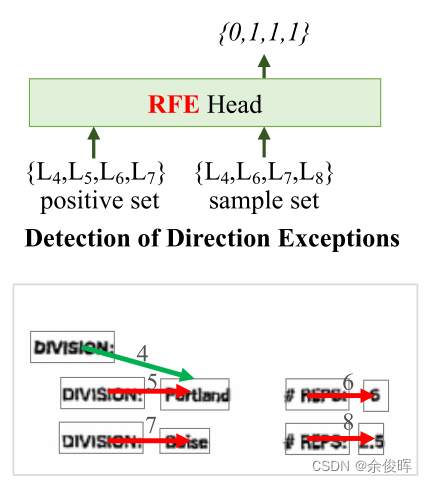
DDE用于GeoMPair（多个文本片段对）的几何预训练。该任务旨在帮助模型捕捉文本片段对之间的常见方向模式，增强对文本片段对的特征表示，并发现那些不符合常规方向模式的片段对。DDE任务包括两个子任务：方向建模和异常检测。方向建模与DDM任务类似，是一个9个方向的分类问题，模型预测两个文本片段之间的方向概率。异常检测是一个二分类问题，用于确定文本片段对是否符合常规方向模式。如果文本片段对不符合常规方向模式，则被视为异常。异常检测使用sigmoid函数应用于一个双线性层，该双线性层以两个文本片段的特征作为输入。损失函数：
$$P^{DDE}=\mathrm{RFE}(S_p,S)$$

$${\mathcal{L}}_{DDE}=\mathrm{BCELoss}(P^{DDE},Y^{DDE})$$

在一个特定的文档区域内的关系通常具有一些共同的几何属性。根据红色键值对的方向，很容易判断绿色的链接方向错误。给定一个超过60%的正集，以及一个样本集，将样本集中的正确对标记为1，而其他方向的对标记为0。

小结：通过在DDE上进行预训练，GeoLayoutLM学习了建模文本片段对之间的几何关系，特别是它们之间的方向关系。

c.Collinearity Identification of Triplet（CIT）

CIT用于GeoTriplet（三个文本片段对）的几何预训练。该任务旨在帮助模型识别三个文本片段是否共线，即它们是否在同一条直线上。CIT任务包括两个子任务：三元组特征表示和共线性识别。三元组特征表示是将三个文本片段的特征相加得到的，因为共线属性是无向的。共线性识别是一个5分类问题，用于确定三个文本片段是否共线。共线性识别使用softmax函数应用于一个线性层，该线性层连接三个文本片段的特征。
$$P_{ijk}^{CIT}=\mathrm{Softmax}(\mathrm{Linear}(B_i+B_j+B_k))$$

$${\mathcal{L}}_{CIT}=\mathrm{CrossEntropy}(P^{CIT},Y^{CIT})$$

给定三个文本段$B_i$、$B_j$和$B_k$，如果$B_i$到$B_j$、$B_j$到$B_k$、$B_i$到$B_k$的方向相同或反相，它们共线；否则不共线的。共线的情况可进一步分为四类：水平线、垂直线、正斜杠和反斜杠。

小结：通过在CIT上进行预训练，GeoLayoutLM学习了建模文本片段之间的几何关系，特别是它们之间的共线关系。

4.3 目标函数

所有预训练任务的总体损失为：
$${\mathcal{L}}_{pt}={\mathcal{L}}_{MVLM}+{\mathcal{L}}_{DDM}+{\mathcal{L}}_{DDE}+{\mathcal{L}}_{CIT}$$

总结

该文章提出GeoLayoutLM，一个用于VIE的几何预训练框架。定义了三种不同层次的几何关系：GeoPair、GeoMPair和GeoTriplet。相应地，引入了三个专门设计的预训练目标来明确地建模几何关系。相较于LayoutLMv3，在关系抽取上取得了非常好的性能，为文档智能的布局理解提供了新的思路。

参考文献

【1】paper：GeoLayoutLM: Geometric Pre-training for Visual Information Extraction

【2】code：https://github.com/AlibabaResearch/AdvancedLiterateMachinery/tree/main/DocumentUnderstanding/GeoLayoutLM