BiMPM实战文本匹配【上】

引言

今天来实现BiMPM模型进行文本匹配，数据集采用的是中文文本匹配数据集。内容较长，分为上下两部分。

数据准备

数据准备这里和之前的模型有些区别，主要是因为它同时有字符词表和单词词表。

from collections import defaultdict
from tqdm import tqdm
import numpy as np
import json
from torch.utils.data import Dataset, DataLoader
import pandas as pd
from typing import Tuple

UNK_TOKEN = "<UNK>"
PAD_TOKEN = "<PAD>"


class Vocabulary:
    """Class to process text and extract vocabulary for mapping"""

    def __init__(self, token_to_idx: dict = None, tokens: list[str] = None) -> None:
        """
        Args:
            token_to_idx (dict, optional): a pre-existing map of tokens to indices. Defaults to None.
            tokens (list[str], optional): a list of unique tokens with no duplicates. Defaults to None.
        """

        assert any(
            [tokens, token_to_idx]
        ), "At least one of these parameters should be set as not None."
        if token_to_idx:
            self._token_to_idx = token_to_idx
        else:
            self._token_to_idx = {}
            if PAD_TOKEN not in tokens:
                tokens = [PAD_TOKEN] + tokens

            for idx, token in enumerate(tokens):
                self._token_to_idx[token] = idx

        self._idx_to_token = {idx: token for token, idx in self._token_to_idx.items()}

        self.unk_index = self._token_to_idx[UNK_TOKEN]
        self.pad_index = self._token_to_idx[PAD_TOKEN]

    @classmethod
    def build(
        cls,
        sentences: list[list[str]],
        min_freq: int = 2,
        reserved_tokens: list[str] = None,
    ) -> "Vocabulary":
        """Construct the Vocabulary from sentences

        Args:
            sentences (list[list[str]]): a list of tokenized sequences
            min_freq (int, optional): the minimum word frequency to be saved. Defaults to 2.
            reserved_tokens (list[str], optional): the reserved tokens to add into the Vocabulary. Defaults to None.

        Returns:
            Vocabulary: a Vocubulary instane
        """

        token_freqs = defaultdict(int)
        for sentence in tqdm(sentences):
            for token in sentence:
                token_freqs[token] += 1

        unique_tokens = (reserved_tokens if reserved_tokens else []) + [UNK_TOKEN]
        unique_tokens += [
            token
            for token, freq in token_freqs.items()
            if freq >= min_freq and token != UNK_TOKEN
        ]
        return cls(tokens=unique_tokens)

    def __len__(self) -> int:
        return len(self._idx_to_token)

    def __getitem__(self, tokens: list[str] | str) -> list[int] | int:
        """Retrieve the indices associated with the tokens or the index with the single token

        Args:
            tokens (list[str] | str): a list of tokens or single token

        Returns:
            list[int] | int: the indices or the single index
        """
        if not isinstance(tokens, (list, tuple)):
            return self._token_to_idx.get(tokens, self.unk_index)
        return [self.__getitem__(token) for token in tokens]

    def lookup_token(self, indices: list[int] | int) -> list[str] | str:
        """Retrive the tokens associated with the indices or the token with the single index

        Args:
            indices (list[int] | int): a list of index or single index

        Returns:
            list[str] | str: the corresponding tokens (or token)
        """

        if not isinstance(indices, (list, tuple)):
            return self._idx_to_token[indices]

        return [self._idx_to_token[index] for index in indices]

    def to_serializable(self) -> dict:
        """Returns a dictionary that can be serialized"""
        return {"token_to_idx": self._token_to_idx}

    @classmethod
    def from_serializable(cls, contents: dict) -> "Vocabulary":
        """Instantiates the Vocabulary from a serialized dictionary


        Args:
            contents (dict): a dictionary generated by `to_serializable`

        Returns:
            Vocabulary: the Vocabulary instance
        """
        return cls(**contents)

    def __repr__(self):
        return f"<Vocabulary(size={len(self)})>"


class TMVectorizer:
    """The Vectorizer which vectorizes the Vocabulary"""

    def __init__(self, vocab: Vocabulary, max_len: int) -> None:
        """
        Args:
            vocab (Vocabulary): maps characters to integers
            max_len (int): the max length of the sequence in the dataset
        """
        self.vocab = vocab
        self.max_len = max_len

    def _vectorize(
        self, indices: list[int], vector_length: int = -1, padding_index: int = 0
    ) -> np.ndarray:
        """Vectorize the provided indices

        Args:
            indices (list[int]): a list of integers that represent a sequence
            vector_length (int, optional): an arugment for forcing the length of index vector. Defaults to -1.
            padding_index (int, optional): the padding index to use. Defaults to 0.

        Returns:
            np.ndarray: the vectorized index array
        """

        if vector_length <= 0:
            vector_length = len(indices)

        vector = np.zeros(vector_length, dtype=np.int64)
        if len(indices) > vector_length:
            vector[:] = indices[:vector_length]
        else:
            vector[: len(indices)] = indices
            vector[len(indices) :] = padding_index

        return vector

    def _get_indices(self, sentence: list[str]) -> list[int]:
        """Return the vectorized sentence

        Args:
            sentence (list[str]): list of tokens
        Returns:
            indices (list[int]): list of integers representing the sentence
        """
        return [self.vocab[token] for token in sentence]

    def vectorize(
        self, sentence: list[str], use_dataset_max_length: bool = True
    ) -> np.ndarray:
        """
        Return the vectorized sequence

        Args:
            sentence (list[str]): raw sentence from the dataset
            use_dataset_max_length (bool): whether to use the global max vector length
        Returns:
            the vectorized sequence with padding
        """
        vector_length = -1
        if use_dataset_max_length:
            vector_length = self.max_len

        indices = self._get_indices(sentence)
        vector = self._vectorize(
            indices, vector_length=vector_length, padding_index=self.vocab.pad_index
        )

        return vector

    @classmethod
    def from_serializable(cls, contents: dict) -> "TMVectorizer":
        """Instantiates the TMVectorizer from a serialized dictionary

        Args:
            contents (dict): a dictionary generated by `to_serializable`

        Returns:
            TMVectorizer:
        """
        vocab = Vocabulary.from_serializable(contents["vocab"])
        max_len = contents["max_len"]
        return cls(vocab=vocab, max_len=max_len)

    def to_serializable(self) -> dict:
        """Returns a dictionary that can be serialized

        Returns:
            dict: a dict contains Vocabulary instance and max_len attribute
        """
        return {"vocab": self.vocab.to_serializable(), "max_len": self.max_len}

    def save_vectorizer(self, filepath: str) -> None:
        """Dump this TMVectorizer instance to file

        Args:
            filepath (str): the path to store the file
        """
        with open(filepath, "w") as f:
            json.dump(self.to_serializable(), f)

    @classmethod
    def load_vectorizer(cls, filepath: str) -> "TMVectorizer":
        """Load TMVectorizer from a file

        Args:
            filepath (str): the path stored the file

        Returns:
            TMVectorizer:
        """
        with open(filepath) as f:
            return TMVectorizer.from_serializable(json.load(f))

先定义词表和向量化的类，然后在分词的时候去掉数字和字母。因为有些数字/字母连在一起非常长，为了防止得到过长的word len。

def tokenize(sentence: str):
    tokens = []
    for word in jieba.cut(sentence):
        if word.isdigit():
            tokens.extend(list(word))
        else:
            tokens.append(word)
    return tokens

同时移除了所有的标点：

def build_dataframe_from_csv(dataset_csv: str) -> pd.DataFrame:
    df = pd.read_csv(
        dataset_csv,
        sep="\t",
        header=None,
        names=["sentence1", "sentence2", "label"],
    )
    # remove all punctuations
    df.sentence1 = df.sentence1.str.replace(r'[^\u4e00-\u9fa50-9]', '', regex=True)
    df.sentence2 = df.sentence2.str.replace(r'[^\u4e00-\u9fa50-9]', '', regex=True)
    df = df.dropna()


    return df

def tokenize_df(df):
    df.sentence1 = df.sentence1.apply(tokenize)
    df.sentence2 = df.sentence2.apply(tokenize)
    return df

我们来看下处理好的结果：

args = Namespace(
        dataset_csv="text_matching/data/lcqmc/{}.txt",
        vectorizer_file="vectorizer.json",
        model_state_file="model.pth",
        save_dir=f"{os.path.dirname(__file__)}/model_storage",
        reload_model=False,
        cuda=False,
        learning_rate=1e-3,
        batch_size=128,
        num_epochs=10,
        max_len=50,
        char_vocab_size=4699,
        word_embedding_dim=300,
        word_vocab_size=35092,
        max_word_len=8,
        char_embedding_dim=20,
        hidden_size=100,
        char_hidden_size=50,
        num_perspective=20,
        num_classes=2,
        dropout=0.2,
        epsilon=1e-8,
        min_word_freq=2,
        min_char_freq=1,
        print_every=500,
        verbose=True,
  )

train_df = build_dataframe_from_csv(args.dataset_csv.format("train"))
test_df = build_dataframe_from_csv(args.dataset_csv.format("test"))
dev_df = build_dataframe_from_csv(args.dataset_csv.format("dev"))

train_df.head()

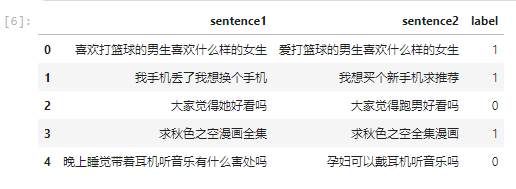
上图是处理后的数据。

接下来先估计字符词表：

train_chars = train_df.sentence1.to_list() + train_df.sentence2.to_list()

char_vocab = Vocabulary.build(train_chars, args.min_char_freq)
# 将词表长度写到参数中
args.char_vocab_size = len(char_vocab)

再进行分词，分词的同时去掉子母和数字：

train_word_df = tokenize_df(train_df)
test_word_df = tokenize_df(test_df)
dev_word_df = tokenize_df(dev_df)

train_sentences = train_df.sentence1.to_list() + train_df.sentence2.to_list()
train_sentences[:10]

[['喜欢', '打篮球', '的', '男生', '喜欢', '什么样', '的', '女生'],
 ['我', '手机', '丢', '了', '我', '想', '换个', '手机'],
 ['大家', '觉得', '她', '好看', '吗'],
 ['求', '秋色', '之空', '漫画', '全集'],
 ['晚上', '睡觉', '带', '着', '耳机', '听', '音乐', '有', '什么', '害处', '吗'],
 ['学', '日语', '软件', '手机', '上', '的'],
 ['打印机', '和', '电脑', '怎样', '连接', '该', '如何', '设置'],
 ['侠盗', '飞车', '罪恶都市', '怎样', '改车'],
 ['什么', '花', '一年四季', '都', '开'],
 ['看图', '猜', '一', '电影', '名']]

接着生成单词词表：

word_vocab = Vocabulary.build(train_sentences, args.min_word_freq)

args.word_vocab_size = len(word_vocab)

args.word_vocab_size

然后找出最长的单词：

words = [word_vocab.lookup_token(idx) for idx in range(args.word_vocab_size)]

longest_word = ''

for word in words:
    if len(word) > len(longest_word):
        longest_word = word

longest_word

'中南财经政法大学'

# 记录下最长单词长度
args.max_word_len = len(longest_word)

char_vectorizer = TMVectorizer(char_vocab, len(longest_word))
word_vectorizer = TMVectorizer(word_vocab, args.max_len)

然后用最长单词长度和自定义的最长句子长度分别构建字符和单词向量化实例。

我们根据这两个TMVectorizer重新设计TMDataset：

from typing import Tuple

class TMDataset(Dataset):
    """Dataset for text matching"""

    def __init__(self, text_df: pd.DataFrame, char_vectorizer: TMVectorizer, word_vectorizer: TMVectorizer) -> None:
        """

        Args:
            text_df (pd.DataFrame): a DataFrame which contains the processed data examples (list of word list)
            vectorizer (TMVectorizer): a TMVectorizer instance
        """

        self.text_df = text_df
        self._char_vectorizer = char_vectorizer
        self._word_vectorizer = word_vectorizer

    def __getitem__(self, index: int) -> Tuple[np.ndarray, np.ndarray, int]:
        row = self.text_df.iloc[index]
        
        
        def vectorize_character(sentence: list[str]) -> np.ndarray:
            # (seq_len, word_len)
            char_vectors = np.zeros(shape=(self._word_vectorizer.max_len, self._char_vectorizer.max_len))
            for idx, word in enumerate(sentence):
                char_vectors[idx] = self._char_vectorizer.vectorize(word)
            
            return char_vectors
        
        self._char_vectorizer.vectorize(row.sentence1),
        self._char_vectorizer.vectorize(row.sentence2),
        
        return (
            self._word_vectorizer.vectorize(row.sentence1),
            self._word_vectorizer.vectorize(row.sentence2),
            vectorize_character(row.sentence1),
            vectorize_character(row.sentence2),
            row.label,
        )

    def get_vectorizer(self) -> Tuple[TMVectorizer, TMVectorizer]:
        return self._word_vectorizer, self._char_vectorizer

    def __len__(self) -> int:
        return len(self.text_df)

多返回了两个char_vectors，它们的形状都是(seq_len, word_len)。

train_dataset = TMDataset(train_df, char_vectorizer, word_vectorizer)
test_dataset = TMDataset(test_df, char_vectorizer, word_vectorizer)
dev_dataset = TMDataset(dev_df, char_vectorizer, word_vectorizer)

for v1, v2, c1, c2, l in train_dataset:
    print(v1.shape)
    print(v2.shape)
    print(c1.shape)
    print(c2.shape)
    print(l)
    break

(50,)
(50,)
(50, 8)
(50, 8)
1

看一下每个样本的形状。

模型实现

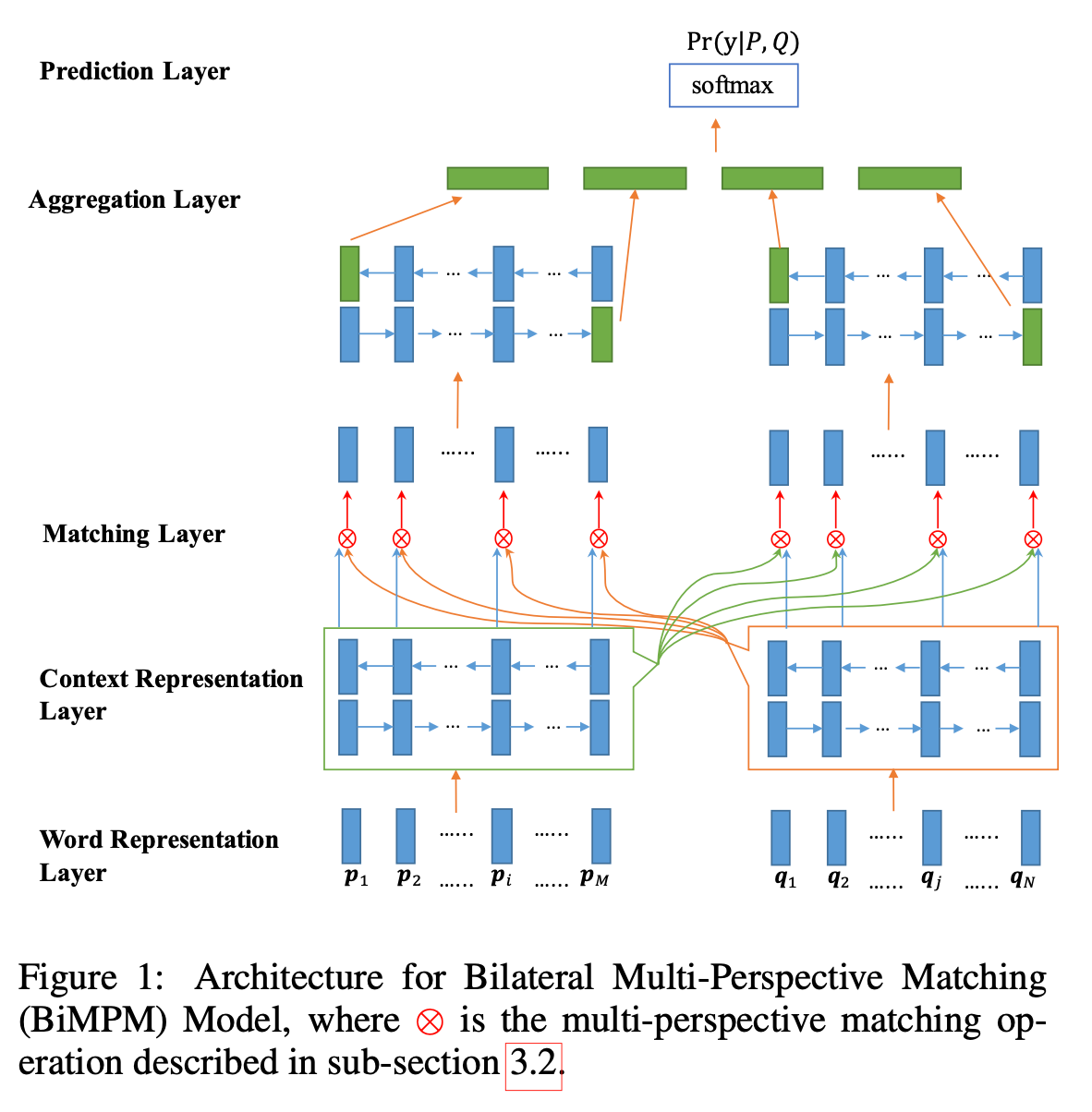
整个模型架构如上图所示，具体的理论部分可以参考引用或自己去读原论文。

我们从底向上依次实现。

单词表征层

该层的目标是用一个 $d$ 维度的向量来表示 $P$ 和 $Q$ 中的每个单词。该向量由两部分组成：一个单词级嵌入和一个字符级嵌入。这里我们的单词级嵌入使用Embedding层来实现，随机初始化来训练。

字符嵌入也是随机初始化可训练的，通过将一个单词中的每个字符(由字符嵌入表示)输入到一个LSTM网络中，用最后一个字符的输出代表整个单词的字符级嵌入。然后和单词级嵌入拼接起来。就得到了该层的输出：两个词向量序列 $P:[\pmb p_1,\cdots,\pmb p_M]$ 和 $Q:[\pmb q_1,\cdots,\pmb q_N]$ 。

class WordRepresentation(nn.Module):
    def __init__(self, args: Namespace) -> None:
        super().__init__()

        self.char_embed = nn.Embedding(
            args.char_vocab_size, args.char_embedding_dim, padding_idx=0
        )

        self.char_lstm = nn.LSTM(
            input_size=args.char_embedding_dim,
            hidden_size=args.char_hidden_size,
            batch_first=True,
        )

        self.word_embed = nn.Embedding(args.word_vocab_size, args.word_embedding_dim)

        self.reset_parameters()

    def reset_parameters(self) -> None:
        nn.init.uniform_(self.char_embed.weight, -0.005, 0.005)
        # zere vectors for padding index
        self.char_embed.weight.data[0].fill_(0)

        nn.init.uniform_(self.word_embed.weight, -0.005, 0.005)

        nn.init.kaiming_normal_(self.char_lstm.weight_ih_l0)
        nn.init.constant_(self.char_lstm.bias_ih_l0, val=0)

        nn.init.orthogonal_(self.char_lstm.weight_hh_l0)
        nn.init.constant_(self.char_lstm.bias_hh_l0, val=0)

    def forward(self, x: Tensor, x_char: Tensor) -> Tensor:
        """

        Args:
            x (Tensor): word input sequence a with shape (batch_size, seq_len)
            x_char (Tensor): character input sequence a with shape (batch_size, seq_len, word_len)

        Returns:
            Tensor: concatenated word and char embedding  (batch_size, seq_len, word_embedding_dim + char_hidden_size)
        """

        batch_size, seq_len, word_len = x_char.shape
        # (batch_size, seq_len, word_len) -> (batch_size * seq_len, word_len)
        x_char = x_char.view(-1, word_len)
        # x_char_embed (batch_size * seq_len, word_len, char_embedding_dim)
        x_char_embed = self.char_embed(x_char)
        # x_char_hidden (1, batch_size * seq_len, char_hidden_size)
        _, (x_char_hidden, _) = self.char_lstm(x_char_embed)

        # x_char_hidden (batch_size, seq_len, char_hidden_size)
        x_char_hidden = x_char_hidden.view(batch_size, seq_len, -1)

        # x_embed (batch_size, seq_len, word_embedding_dim),
        x_embed = self.word_embed(x)

        # (batch_size, seq_len, word_embedding_dim + char_hidden_size)
        return torch.cat([x_embed, x_char_hidden], dim=-1)

字符嵌入需要一个Embedding层和一个单向LSTM层；单词嵌入只需要定义一个Embedding层。

本模型的参数初始化挺重要的，对这些网络层不同的参数分别进行了初始化。其中正交初始化(nn.init.orthogonal_)可以缓解LSTM中的梯度消失/爆炸问题、改善收敛性、提高模型的泛化能力、降低参数的冗余性。

注意WordRepresentation层是单独作用于不同的语句的，每个语句进行单词级拆分和字符级拆分。

在计算字符级嵌入时，首先将x_char的形状变为(batch_size * seq_len, word_len)，可以理解增大了批大小，word_len是最长单词长度；然后输入到char_embed中得到字符嵌入；最后再喂给char_lstm并用最后一个时间步(最后一个字符)对应的状态表示对应的单词的字符级嵌入。

然后把单词的字符级嵌入恢复成原来的形状，即batch_size, seq_len, char_hidden_size。

这样就可以和单词嵌入(batch_size, seq_len, word_embedding_dim)进行在最后一个维度上拼接。

即融合了单词和字符级信息的表征。

上下文表示层

上下文表示层(Context Representation Layer) 使用一个BiLSTM合并上下文信息到 $P$ 和 $Q$ 的每个时间步的表示中。

class ContextRepresentation(nn.Module):
    def __init__(self, args: Namespace) -> None:
        super().__init__()
        self.context_lstm = nn.LSTM(
            input_size=args.word_embedding_dim + args.char_hidden_size,
            hidden_size=args.hidden_size,
            batch_first=True,
            bidirectional=True,
        )

        self.reset_parameters()

    def reset_parameters(self) -> None:
        nn.init.kaiming_normal_(self.context_lstm.weight_ih_l0)
        nn.init.constant_(self.context_lstm.bias_ih_l0, val=0)
        nn.init.orthogonal_(self.context_lstm.weight_hh_l0)
        nn.init.constant_(self.context_lstm.bias_hh_l0, val=0)

        nn.init.kaiming_normal_(self.context_lstm.weight_ih_l0_reverse)
        nn.init.constant_(self.context_lstm.bias_ih_l0_reverse, val=0)
        nn.init.orthogonal_(self.context_lstm.weight_hh_l0_reverse)
        nn.init.constant_(self.context_lstm.bias_hh_l0_reverse, val=0)

    def forward(self, x: Tensor) -> Tensor:
        """
        Compute the contextual information about input.
        Args:
            x (Tensor): (batch_size, seq_len, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len, 2 * hidden_size)
        """

        # (batch_size, seq_len, 2 * hidden_size)
        return self.context_lstm(x)[0]

该层的实现和简单，注意它的LSTM输入大小是低层的输出大小，也是独立应用于每个语句的。

匹配层

匹配层(Matching Layer) 这是该模型的核心层，也是最复杂的。

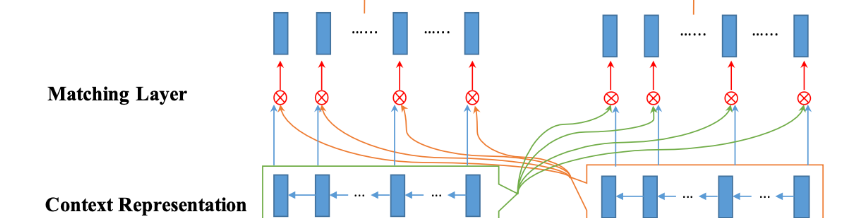
目标是用一个句子的每个上下文嵌入(时间步)和另一个句子的所有上下文嵌入(时间步)进行比较。如上图所示，我们会从两个方向匹配 $P$ 和 $Q$ ：对于 $P$ 来说， $P$ 的每个时间步都会和 $Q$ 所有时间步进行匹配，然后 $Q$ 的每个时间步也会和 $P$ 所有时间步进行匹配。

为了让一个句子的一个时间步与另一个的所有时间步进行匹配，作者设计了一个多视角匹配操作 $\otimes$ 。该层的输出是两个匹配向量序列，每个序列为一个句子一个时间步与另一个所有时间步的匹配结果。

通过以下两步来定义多视角匹配操作 $\otimes$ ：

① 定义一个多视角余弦匹配函数 $f_m$ 来比较两个向量：
$\pmb m = f_m(\pmb v_1,\pmb v_2;W) \tag 1$
这里 $v1 \pmb v_1$ 和 $v2 \pmb v_2$ 是两个 $d$ 维的向量； $\in \R^{l \times d}$ 是一个可训练的参数； $l$ 是视角数；返回的 $\pmb m$ 是一个 $l$ 维的向量 $\pmb m= [m_1,\cdots,m_k,\cdots,m_l]$ 。

其中每个元素 $m_k \in \pmb m$ 是第 $k$ 个视角的匹配值(标量)，它是通过计算两个加权向量余弦相似度得到的：
$m_k = \cos(W_k \circ \pmb v_1,W_k \circ \pmb v_2) \tag 2$
这里 $\circ$ 是元素级乘法； $W_k$ 是 $W$ 的第 $k$ 行，它控制了第 $k$ 个视角并且为 $d$ 维空间的不同维度分配了不同的权重。

把公式 $(1)$ 展开来就是：
$f_m(\pmb v_1,\pmb v_2;W)=\begin{bmatrix} m_1 \\ \cdots \\ m_k \\ \cdots \\ m_l \end{bmatrix} = \begin{bmatrix} \cos(W_1 \circ \pmb v_1,W_1 \circ \pmb v_2) \\ \cdots \\ \cos(W_k \circ \pmb v_1,W_k \circ \pmb v_2) \\ \cdots \\ \cos(W_l \circ \pmb v_1,W_l \circ \pmb v_2) \\ \end{bmatrix} \in \R^l \tag 3$
这里的 $l$ 是超参数，对应不同的权重。

简单来说就是计算两个向量的余弦相似度，但这两个向量是经过加权( $W_i \circ v,\quad i \in \{1,\cdots,l\}$ )之后的结果。有多少个权重是由 $l$ 控制的，每次加权的参数不同，相当于不同的视角。总共有 $l$ 个视角。希望用权重(视角)去控制比较这两个向量不同的方面。

下面来看第二步。

②基于上面这个匹配函数，定义了四种匹配策略:

全匹配(Full-Matching)
最大池匹配(Maxpooling-Matching)
注意力匹配(Attentive-Matching)
最大注意力匹配(Max-Attentive-Matching)

全匹配

如下图所示，在该策略中，每个句子的正向(或反向)上下文嵌入 $\overset{\rightarrow}{\pmb h_i^p}$ (或 $\overset{\leftarrow}{\pmb h_i^p}$ )都与另一句的正向(或反向)的最后一个时间步表示 $\overset{\rightarrow}{\pmb h_N^q}$ (或 $\overset{\leftarrow}{\pmb h_1^q}$ )进行比较：

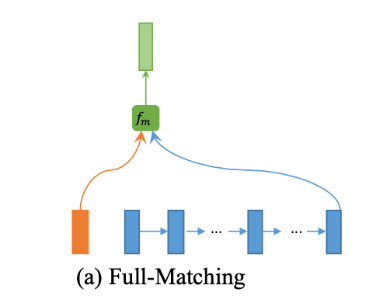
比如 $Q$ 句子正向上所有时间步的嵌入要比较的是 $P$ 正向上最后一个时间步。

公式如下：

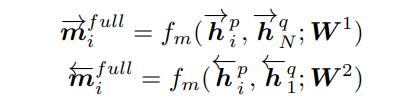
根据公式实现全匹配如下：

    def _full_matching(self, v1: Tensor, v2_last: Tensor, w: Tensor) -> Tensor:
        """full matching operation.

        Args:
            v1 (Tensor): the full embedding vector sequence (batch_size, seq_len1, hidden_size)
            v2_last (Tensor): single embedding vector (batch_size, hidden_size)
            w (Tensor): weights of one direction (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len1, num_perspective)
        """

        # (batch_size, seq_len1, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        # (batch_size, num_perspective, hidden_size)
        v2 = self._time_distributed_multiply(v2_last, w)
        # (batch_size, 1, num_perspective, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, num_perspective)
        return self._cosine_similarity(v1, v2)

如函数所示，它接收两个参数，分别是某个方向上(正向或反向)一个包含所有时间步的完整序列向量，和另一个同方向上最后一个时刻的向量。

如公式 $(3)$ 所示，分别让这两个向量乘以多视角权重 $\in \R^{l \times d}$ ，这里调用_time_distributed_multiply来实现。最后调用_cosine_similarity计算它们之间的余弦相似度。

  def _time_distributed_multiply(self, x: Tensor, w: Tensor) -> Tensor:
        """element-wise multiply vector and weights.

        Args:
            x (Tensor): sequence vector (batch_size, seq_len, hidden_size) or singe vector (batch_size, hidden_size)
            w (Tensor): weights (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len, num_perspective, hidden_size) or (batch_size, num_perspective, hidden_size)
        """

        # dimension of x
        n_dim = x.dim()
        hidden_size = x.size(-1)
        # if n_dim == 3
        seq_len = x.size(1)

        # (batch_size * seq_len, hidden_size) for n_dim == 3
        # (batch_size, hidden_size) for n_dim == 2
        x = x.contiguous().view(-1, hidden_size)

        # (batch_size * seq_len, 1, hidden_size) for n_dim == 3
        # (batch_size, 1, hidden_size) for n_dim == 2
        x = x.unsqueeze(1)

        # (1, num_perspective, hidden_size)
        w = w.unsqueeze(0)

        # (batch_size * seq_len, num_perspective, hidden_size) for n_dim == 3
        # (batch_size, num_perspective, hidden_size) for n_dim == 2
        x = x * w

        # reshape to original shape
        if n_dim == 3:
            # (batch_size, seq_len, num_perspective, hidden_size)
            x = x.view(-1, seq_len, self.l, hidden_size)
        elif n_dim == 2:
            # (batch_size, num_perspective, hidden_size)
            x = x.view(-1, self.l, hidden_size)
        # (batch_size, seq_len, num_perspective, hidden_size) for n_dim == 3
        # (batch_size, num_perspective, hidden_size) for n_dim == 2
        return x

_time_distributed_multiply可以接收不同形状的向量，num_perspective是视角数，也就是原文中的l，为了和1进行区分，这里用完整名称表示。

首先查看输入向量的x形状，如果有3个维度，我们还要记录它的seq_len大小。

然后转换成(-1, hidden_size)的形状，接着变成(?, 1, hidden_size)的维度，这里?根据n_dim有所区分，具体可以参考注释。

接着为了进行广播，在w上也插入一个维度，变成 (1, num_perspective, hidden_size)。

广播的时候x会变成(?, num_perspective, hidden_size)；w会变成(?, num_perspective, hidden_size)。

这样x * w实际上是逐元素相乘。

最后还原成原来x的形状(batch_size, seq_len, num_perspective, hidden_size)或x.view(-1, self.l, hidden_size)，但多了个视角数num_perspective。

此时的这个待返回的x已经是乘以不同视角权重后的结果。

我们把眼光回到_full_matching中，

# (batch_size, seq_len1, num_perspective, hidden_size)
v1 = self._time_distributed_multiply(v1, w)

v2 = self._time_distributed_multiply(v2_last, w)
# (batch_size, 1, num_perspective, hidden_size)
v2 = v2.unsqueeze(1)

# (batch_size, seq_len1, num_perspective)
return self._cosine_similarity(v1, v2)

同样为了进行广播，对v2插入相应的维度，变成了 (batch_size, 1, num_perspective, hidden_size)，那个1会被复制seq_len1次。

最后调用_cosine_similarity计算它们之间的余弦相似度。

    def _cosine_similarity(self, v1: Tensor, v2: Tensor) -> Tensor:
        """compute cosine similarity between v1 and v2.
        Args:
            v1 (Tensor): (..., hidden_size)
            v2 (Tensor): (..., hidden_size)

        Returns:
            Tensor: _description_
        """
        # element-wise multiply
        cosine = v1 * v2
        # caculate on hidden_size dimenstaion
        # (batch_size, seq_len, l)
        cosine = cosine.sum(-1)
        # caculate on hidden_size dimenstaion
        # (batch_size, seq_len, l)
        v1_norm = torch.sqrt(torch.sum(v1**2, -1).clamp(min=self.epsilon))
        # (batch_size, seq_len, l)
        v2_norm = torch.sqrt(torch.sum(v2**2, -1).clamp(min=self.epsilon))
        # (batch_size, seq_len, l)
        return cosine / (v1_norm * v2_norm)

我们以上面的例子继续分析，这里v1的形状是(batch_size, seq_len1, num_perspective, hidden_size)，v2也被会广播成(batch_size, seq_len1, num_perspective, hidden_size)。

根据余弦相似度的公式，首先计算这两个向量的点积，然后除以这两个向量的模。

第一步是计算这两个向量的点积，首先进行逐元素乘法，得到(batch_size, seq_len1, num_perspective, hidden_size)的结果，然后求和，得到(batch_size, seq_len1, num_perspective)的结果。

可以看成是有batch_size * seq_len1 * num_perspective个向量对进行点积运算，每个向量的维度是100维，cosine = cosine.sum(-1)就得到batch_size * seq_len1 * num_perspective个标量(点积结果)。

也可以理解为两个(batch_size, seq_len1, num_perspective, hidden_size)的向量在hidden_size维度上计算点积。

接下来分别计算这两个向量的模，可能结果非常小接近零，防止过小，设定了最小为sefl.epsilon。

最后就是点积除以模，得到余弦相似度的值。

下面来看最大池化匹配。

最大池化匹配

如下图所示，在这种策略中，每个正向(或反向)上下文嵌入 $\overset{\rightarrow}{\pmb h_i^p}$ (或 $\overset{\leftarrow}{\pmb h_i^p}$ )都与另一句的每个正向(或反向)上下文嵌入 $\overset{\rightarrow}{\pmb h_j^q}$ (或 $\overset{\leftarrow}{\pmb h_j^q}$ , 其中 $\in (1,\cdots N)$ ) 进行比较，然后只保留每个维度的最大值。

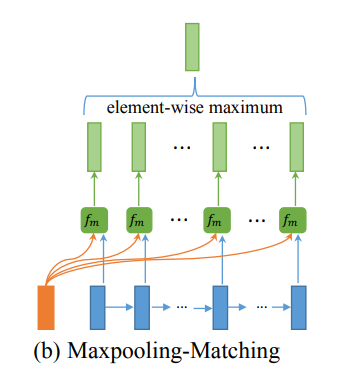
公式为：

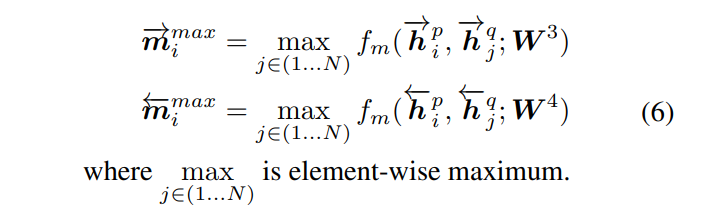
理解了全匹配之后应该不难理解这个最大池化匹配。

这次在这两个向量序列之间互相计算，也是在最后一个维度hidden_size上计算。

首先分别得到加权后的向量，然后这两个向量计算余弦相似度，最后在第二个向量的seq_len维度上找到最大的值。没了。

    def _max_pooling_matching(self, v1: Tensor, v2: Tensor, w: Tensor) -> Tensor:
        """max pooling matching operation.

        Args:
            v1 (Tensor): (batch_size, seq_len1, hidden_size)
            v2 (Tensor): (batch_size, seq_len2, hidden_size)
            w (Tensor): (num_perspective, hidden_size)

        Returns:
            Tensor: (batch_size, seq_len1, num_perspective)
        """

        # (batch_size, seq_len1, num_perspective, hidden_size)
        v1 = self._time_distributed_multiply(v1, w)
        # (batch_size, seq_len2, num_perspective, hidden_size)
        v2 = self._time_distributed_multiply(v2, w)
        # (batch_size, seq_len1, 1, num_perspective, hidden_size)
        v1 = v1.unsqueeze(2)
        # (batch_size, 1, seq_len2, num_perspective, hidden_size)
        v2 = v2.unsqueeze(1)
        # (batch_size, seq_len1, seq_len2, num_perspective)
        cosine = self._cosine_similarity(v1, v2)
        # (batch_size, seq_len1, num_perspective)
        return cosine.max(2)[0]

为了计算这两个向量之间的余弦相似度，分别需要插入新维度，变成(batch_size, seq_len1, seq_len2, num_perspective, hidden_size)的形式。

调用_cosine_similarity计算余弦相似度后，形状变成了 (batch_size, seq_len1, seq_len2, num_perspective)。然后取第二个向量序列维度上的最大值，即cosine.max(2)，它会返回一个value和index，通过[0]取它的value。