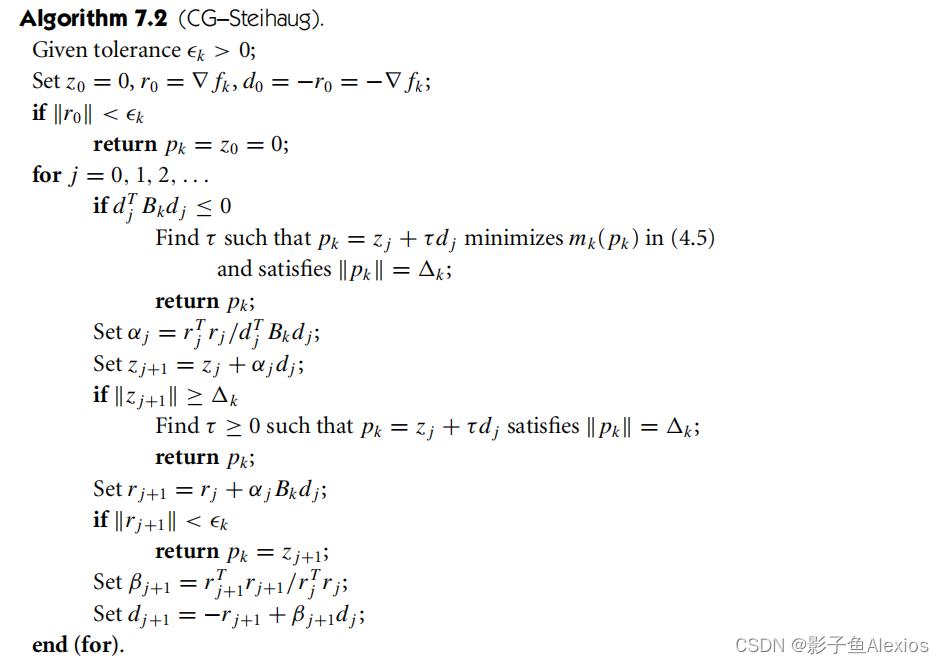机器人中的数值优化|【七】线性搜索牛顿共轭梯度法、可信域牛顿共轭梯度法 Line Search Newton-CG, Trust Region Newton-CG

往期回顾

机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法，可行牛顿法的python实现，以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化，拟牛顿法理论与推导
机器人中的数值优化|【四】L-BFGS理论推导与延伸
机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
机器人中的数值优化|【六】线性共轭梯度法，牛顿共轭梯度法

线性搜索牛顿共轭梯度法 Line Search Newton-CG

线性搜索牛顿-CG方法，也称为截断牛顿方法。最基础的Newton step是通过求解线性系统的方程${\nabla }^2{f}_k{d}_k^N=-\nabla f_k$来实现的。然而，CG方法是用来求解正定系统的，当$x_k$不接近解时，hessian阵${\nabla }^2{f}_k$可能具有负特征值。因此，一旦产生了一个负曲率的方向，我们就终止了CG迭代。

可信域牛顿共轭梯度法 Trust Region Newton Conjugate Gradient Method