机器人中的数值优化|【四】L-BFGS理论推导与延伸
往期内容回顾
机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化,拟牛顿法理论与推导
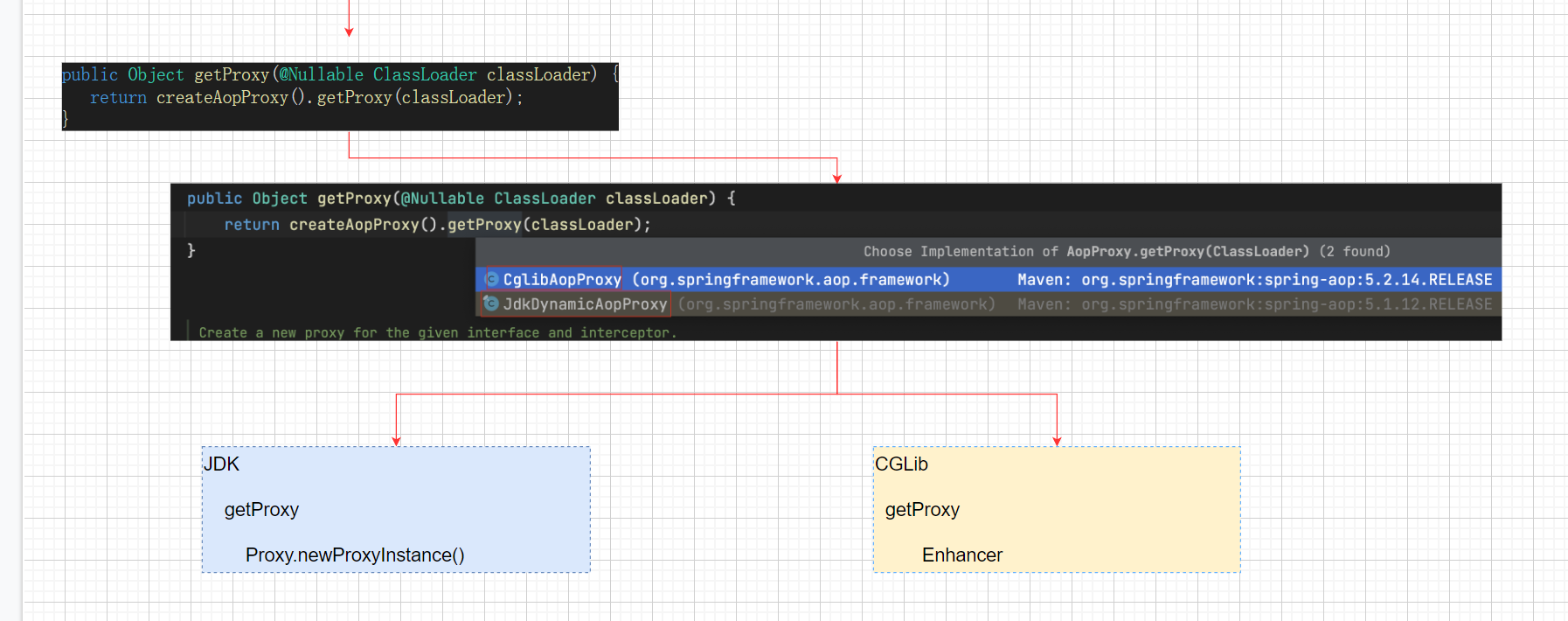
L-BFGS方法
在上一节中我们对拟牛顿法进行了详细的推导,特别是对BFGS的推导过程比较熟悉了,我们发现BFGS虽然解决了牛顿法中hessian可能不存在以及hessian求逆计算复杂的通电,但是在大规模优化过程中,很可能没有办法去存储一个
n
×
n
n \times n
n×n矩阵,因此Limited memory GFGS算法自然而然就被提出,表示使用有限的空间来进行计算。观察原来的式子
Δ
B
t
=
Δ
g
t
Δ
g
t
T
Δ
x
t
Δ
g
t
T
−
B
t
Δ
x
t
Δ
x
t
T
B
t
T
Δ
x
t
T
Δ
B
t
T
Δ
x
t
\Delta B_t = \frac{\Delta g_t \Delta g_t^T}{\Delta x_t \Delta g_t^T} - \frac{B_t \Delta x_t \Delta x_t^T B_t^T}{\Delta x_t^T \Delta B_t^T \Delta x_t}
ΔBt=ΔxtΔgtTΔgtΔgtT−ΔxtTΔBtTΔxtBtΔxtΔxtTBtT
B
t
+
1
−
1
=
(
I
n
−
Δ
x
Δ
g
T
Δ
x
t
T
Δ
g
t
)
B
t
−
1
(
I
n
−
Δ
g
t
Δ
x
t
T
Δ
x
t
T
Δ
g
t
)
+
Δ
x
t
Δ
x
t
T
Δ
x
t
T
Δ
g
t
B_{t+1}^{-1} = (I_n - \frac{\Delta x \Delta g^T}{\Delta x_t^T \Delta g_t})B_t^{-1}(I_n - \frac{\Delta g_t \Delta x_t^T}{\Delta x_t^T \Delta g_t}) + \frac{\Delta x_t \Delta x_t^T}{\Delta x_t^T \Delta g_t}
Bt+1−1=(In−ΔxtTΔgtΔxΔgT)Bt−1(In−ΔxtTΔgtΔgtΔxtT)+ΔxtTΔgtΔxtΔxtT
我们很容易知道,
B
t
+
1
B_{t+1}
Bt+1可以通过迭代计算
Δ
x
t
,
Δ
g
t
\Delta x_t,\Delta g_t
Δxt,Δgt来得到,LBFGS的思想是不再使用所有的
Δ
x
t
,
Δ
g
t
\Delta x_t,\Delta g_t
Δxt,Δgt,而是通过使用最近的
m
m
m个序列来计算。这样只需要保存
2
m
2m
2m个向量,然后每次迭代最近的结果即可计算出近似矩阵
B
B
B,避免显式保存矩阵信息。
令
ρ
k
=
1
Δ
x
k
T
Δ
g
k
\rho_k = \frac{1}{\Delta x_k^T \Delta g_k}
ρk=ΔxkTΔgk1
V
k
=
I
−
ρ
k
Δ
x
k
Δ
g
k
T
V_k = I -\rho_k \Delta x_k \Delta g_k^T
Vk=I−ρkΔxkΔgkT
可以简写为
B
t
+
1
−
1
=
V
k
B
t
−
1
V
k
T
+
ρ
k
Δ
x
t
Δ
x
t
T
B_{t+1}^{-1} = V_kB_{t}^{-1}V_k^T + \rho_k \Delta x_t \Delta x_t^T
Bt+1−1=VkBt−1VkT+ρkΔxtΔxtT
实际工程应用中,可以使用two-loop recursion方法,直接计算得到搜索方向,不用显示计算矩阵,如下所示: