1 E矩阵
1.1 由F到E
E = K T ∗ F ∗ K E = K^T * F * K E=KT∗F∗K
E 矩阵可以直接通过之前算好的 F 矩阵与相机内参 K 矩阵获得
Mat E = K.t() * F * K;
相机内参获得的方式是一个较为复杂的方式,需要使用棋盘进行定位获得,我们这里直接使用了 OpenMVG 提供的现成的图片和 K 矩阵
1.2 直接使用函数
利用 openCV 提供的 findEssentialMat 函数可以直接得到 E 矩阵
Mat E = findEssentialMat(matchedPoints1, matchedPoints2, K, RANSAC, 0.999, 1.0, inliers);
2 相机姿态恢复
这一步可以使用 SVD 来通过 E 矩阵获取相对旋转矩阵 R 和平移向量 t
但是OpenCV直接提供了一个非常便捷的函数 —— recoverPose
其接受本质矩阵 E 、特征点的对应关系、相机的内参信息以及输出的相对旋转矩阵 R 和平移向量 t ;它会自动进行 SVD 分解和其他必要的计算,以恢复相对姿态信息
//相机姿态恢复,求解R,t,投影矩阵
Mat R, t;
recoverPose(E, inlierPoints1, inlierPoints2, K, R, t);
3 相机投影矩阵
要构建相机的投影矩阵(也称为视图矩阵或外参矩阵),需要将旋转矩阵 R 和平移向量 t 合并到一起,投影矩阵通常表示为 3x4 的矩阵,其中旋转矩阵和平移向量都位于其中的适当位置
通常情况下,投影矩阵的形式如下:
P
1
=
K
∗
[
R
∣
t
]
P_1 = K * [R | t]
P1=K∗[R∣t]
P 2 = K ∗ [ I ∣ 0 ] P_2 = K * [I | 0] P2=K∗[I∣0]
实现代码如下:
// 创建两个相机的投影矩阵 [R T]
Mat proj1(3, 4, CV_32FC1);
Mat proj2(3, 4, CV_32FC1);
// 设置第一个相机的投影矩阵为单位矩阵 [I | 0]
proj1(Range(0, 3), Range(0, 3)) = Mat::eye(3, 3, CV_32FC1);
proj1.col(3) = Mat::zeros(3, 1, CV_32FC1);
// 设置第二个相机的投影矩阵为输入的旋转矩阵 R 和平移向量 T
R.convertTo(proj2(Range(0, 3), Range(0, 3)), CV_32FC1);
t.convertTo(proj2.col(3), CV_32FC1);
// 转换相机内参矩阵 K 为浮点型
Mat fK;
K.convertTo(fK, CV_32FC1);
// 计算投影矩阵 [K * [R|T]]
proj1 = fK * proj1;
proj2 = fK * proj2;
4 三角法得稀疏点云
4.1 三角法计算3D点
对于每对匹配的特征点,可以使用三角法来计算它们的三维坐标;这通常涉及到将两个视角下的像素坐标与相应的投影矩阵相结合,以恢复三维坐标
// 三角法求解稀疏三维点云
Mat point4D_homogeneous(4, inlierPoints1.size(), CV_64F);
triangulatePoints(proj1, proj2, inlierPoints1, inlierPoints2, point4D_homogeneous);
4.2 转换为非齐次坐标
函数 triangulatePoints 得到的 point4D_homogeneous 通常是齐次坐标,需要将它们转换为非齐次坐标,以得到真实的三维点坐标
// 将齐次坐标转换为三维坐标
Mat point3D;
convertPointsFromHomogeneous(point4D_homogeneous.t(), point3D);
cout << point3D << endl;
5 匹配颜色
将颜色信息与点云关联在一起
使用了内点(inliers)的坐标从图像中提取了颜色信息,然后将颜色信息与三维点坐标关联起来,生成了带有颜色的稀疏点云
并将其存储在 pointCloud 和 pointColors 中;就可以根据需要进一步处理颜色信息
// 获取特征点的颜色信息
vector<Vec3b> colors1, colors2; // 颜色信息
for (Point2f& inlierPoints : inlierPoints1)
{
int x = cvRound(inlierPoints.x); // 关键点的x坐标
int y = cvRound(inlierPoints.y); // 关键点的y坐标
Vec3b color = img1.at<Vec3b>(y, x);
colors1.push_back(color);
}
for (Point2f& inlierPoints : inlierPoints2)
{
int x = cvRound(inlierPoints.x); // 关键点的x坐标
int y = cvRound(inlierPoints.y); // 关键点的y坐标
Vec3b color = img2.at<Vec3b>(y, x);
colors2.push_back(color);
}
// 创建带颜色的点云数据结构
vector<Point3f> pointCloud;
vector<Vec3b> pointColors;
// 关联颜色信息到点云
for (int i = 0; i < point3D.rows; ++i)
{
Point3f point = point3D.at<Point3f>(i);
Vec3b color1 = colors1[i];
Vec3b color2 = colors2[i];
// 在这里可以根据需要选择使用哪个颜色,或者进行颜色插值等处理
Vec3b finalColor = color1; // 这里示例使用第一个相机的颜色
pointCloud.push_back(point);
pointColors.push_back(finalColor);
}
6 生成 ply 文件
手动输出点云 PLY 文件,并包括了 PLY 文件的头部信息以及点云数据的写入;这是一种创建包含颜色信息的 PLY 文件的有效方法
在 PLY 文件的头部信息中,指定了点的数量以及点的属性,包括点的坐标和颜色通道(蓝色、绿色、红色)然后,你循环遍历点云数据,将点的坐标和颜色信息写入PLY文件
其会生成一个包含点云和颜色信息的PLY文件,可以将其用于保存点云以进行可视化或进一步处理
特别注意:图片是RGB还是BGR的颜色通道,这里是RGB
color[0],color[1],color[2]分别代表蓝色,绿色,红色通道
// 手动输出点云ply文件
ofstream plyFile(PLY_SAVE_PATH);
// ply的头部信息
plyFile << "ply\n";
plyFile << "format ascii 1.0\n";
plyFile << "element vertex " << point3D.rows << "\n";
plyFile << "property float x\n";
plyFile << "property float y\n";
plyFile << "property float z\n";
plyFile << "property uchar blue\n";
plyFile << "property uchar green\n";
plyFile << "property uchar red\n";
plyFile << "end_header\n";
// 写入点云数据
for (int i = 0; i < point3D.rows; ++i)
{
Vec3b color = pointColors[i];
const float* point = point3D.ptr<float>(i);
plyFile << point[0] << " " << point[1] << " " << point[2] << " "
<< static_cast<int>(color[0]) << " "
<< static_cast<int>(color[1]) << " "
<< static_cast<int>(color[2]) << endl;
}
plyFile.close();
7 完整测试代码
关于之前的阶段可以查看我之前的文章
// 定义图像文件路径和保存结果的路径
#define IMG_PATH1 "test_img\\images\\100_7105.jpg"
#define IMG_PATH2 "test_img\\images\\100_7106.jpg"
#define PLY_SAVE_PATH "test_img\\results\\output.ply"
#define K_NUM 2905.88, 0, 1416, 0, 2905.88, 1064, 0, 0, 1 // 3*3
#include <opencv2/opencv.hpp>
#include <iostream>
#include <vector>
#include <fstream>
using namespace std;
using namespace cv;
int main()
{
// 阶段一------------------------------------------------------------------------------------
// 读取两幅图像
Mat img1 = imread(IMG_PATH1);
Mat img2 = imread(IMG_PATH2);
if (img1.empty() || img2.empty())
{
cout << "无法读取图像" << endl;
return -1;
}
// 创建SIFT对象
Ptr<SIFT> sift = SIFT::create();
vector<KeyPoint> keypoints1, keypoints2;
Mat descriptors1, descriptors2;
// 检测关键点并计算描述子
sift->detectAndCompute(img1, noArray(), keypoints1, descriptors1);
sift->detectAndCompute(img2, noArray(), keypoints2, descriptors2);
// 使用FLANN进行特征匹配
FlannBasedMatcher matcher;
vector<vector<DMatch>> matches;
matcher.knnMatch(descriptors1, descriptors2, matches, 2);
vector<DMatch> good_matches;
for (int i = 0; i < matches.size(); ++i)
{
const float ratio = 0.7f;
if (matches[i][0].distance < ratio * matches[i][1].distance)
{
good_matches.push_back(matches[i][0]);
}
}
// 阶段二------------------------------------------------------------------------------------
// 声明用于保存匹配点对的容器
vector<Point2f> matchedPoints1, matchedPoints2;
for (int i = 0; i < good_matches.size(); ++i)
{
matchedPoints1.push_back(keypoints1[good_matches[i].queryIdx].pt);
matchedPoints2.push_back(keypoints2[good_matches[i].trainIdx].pt);
}
// 进行基本矩阵F的估计并使用RANSAC筛选
Mat F;
vector<uchar> inliers;
F = findFundamentalMat(matchedPoints1, matchedPoints2, inliers, FM_RANSAC);
cout << F << endl;
vector<Point2f> inlierPoints1;
vector<Point2f> inlierPoints2;
for (int i = 0; i < inliers.size(); ++i)
{
if (inliers[i])
{
inlierPoints1.push_back(matchedPoints1[i]);
inlierPoints2.push_back(matchedPoints2[i]);
}
}
// 相机内参矩阵K
Mat K = (Mat_<double>(3, 3) << K_NUM);
cout << K << endl;
计算本质矩阵E
//Mat E = findEssentialMat(matchedPoints1, matchedPoints2, K, RANSAC, 0.999, 1.0, inliers);
Mat E = K.t() * F * K;
cout << "Essential Matrix (E):" << endl;
cout << E << endl;
//相机姿态恢复,求解R,t,投影矩阵
Mat R, t;
recoverPose(E, inlierPoints1, inlierPoints2, K, R, t);
cout << "recoverpose" << endl;
cout << "R:" << R << endl;
cout << "t:" << t << endl;
// 创建两个相机的投影矩阵 [R T]
Mat proj1(3, 4, CV_32FC1);
Mat proj2(3, 4, CV_32FC1);
// 设置第一个相机的投影矩阵为单位矩阵 [I | 0]
proj1(Range(0, 3), Range(0, 3)) = Mat::eye(3, 3, CV_32FC1);
proj1.col(3) = Mat::zeros(3, 1, CV_32FC1);
// 设置第二个相机的投影矩阵为输入的旋转矩阵 R 和平移向量 T
R.convertTo(proj2(Range(0, 3), Range(0, 3)), CV_32FC1);
t.convertTo(proj2.col(3), CV_32FC1);
// 转换相机内参矩阵 K 为浮点型
Mat fK;
K.convertTo(fK, CV_32FC1);
// 计算投影矩阵 [K * [R|T]]
proj1 = fK * proj1;
proj2 = fK * proj2;
// 三角法求解稀疏三维点云
Mat point4D_homogeneous(4, inlierPoints1.size(), CV_64F);
triangulatePoints(proj1, proj2, inlierPoints1, inlierPoints2, point4D_homogeneous);
// 将齐次坐标转换为三维坐标
Mat point3D;
convertPointsFromHomogeneous(point4D_homogeneous.t(), point3D);
cout << point3D << endl;
// 获取特征点的颜色信息
vector<Vec3b> colors1, colors2; // 颜色信息
for (Point2f& inlierPoints : inlierPoints1)
{
int x = cvRound(inlierPoints.x); // 关键点的x坐标
int y = cvRound(inlierPoints.y); // 关键点的y坐标
Vec3b color = img1.at<Vec3b>(y, x);
colors1.push_back(color);
}
for (Point2f& inlierPoints : inlierPoints2)
{
int x = cvRound(inlierPoints.x); // 关键点的x坐标
int y = cvRound(inlierPoints.y); // 关键点的y坐标
Vec3b color = img2.at<Vec3b>(y, x);
colors2.push_back(color);
}
// 创建带颜色的点云数据结构
vector<Point3f> pointCloud;
vector<Vec3b> pointColors;
// 关联颜色信息到点云
for (int i = 0; i < point3D.rows; ++i)
{
Point3f point = point3D.at<Point3f>(i);
Vec3b color1 = colors1[i];
Vec3b color2 = colors2[i];
// 在这里可以根据需要选择使用哪个颜色,或者进行颜色插值等处理
Vec3b finalColor = color1; // 这里示例使用第一个相机的颜色
pointCloud.push_back(point);
pointColors.push_back(finalColor);
}
// 手动输出点云ply文件
ofstream plyFile(PLY_SAVE_PATH);
// ply的头部信息
plyFile << "ply\n";
plyFile << "format ascii 1.0\n";
plyFile << "element vertex " << point3D.rows << "\n";
plyFile << "property float x\n";
plyFile << "property float y\n";
plyFile << "property float z\n";
plyFile << "property uchar blue\n";
plyFile << "property uchar green\n";
plyFile << "property uchar red\n";
plyFile << "end_header\n";
// 写入点云数据
for (int i = 0; i < point3D.rows; ++i)
{
Vec3b color = pointColors[i];
const float* point = point3D.ptr<float>(i);
plyFile << point[0] << " " << point[1] << " " << point[2] << " "
<< static_cast<int>(color[0]) << " "
<< static_cast<int>(color[1]) << " "
<< static_cast<int>(color[2]) << endl;
}
plyFile.close();
return 0;
}
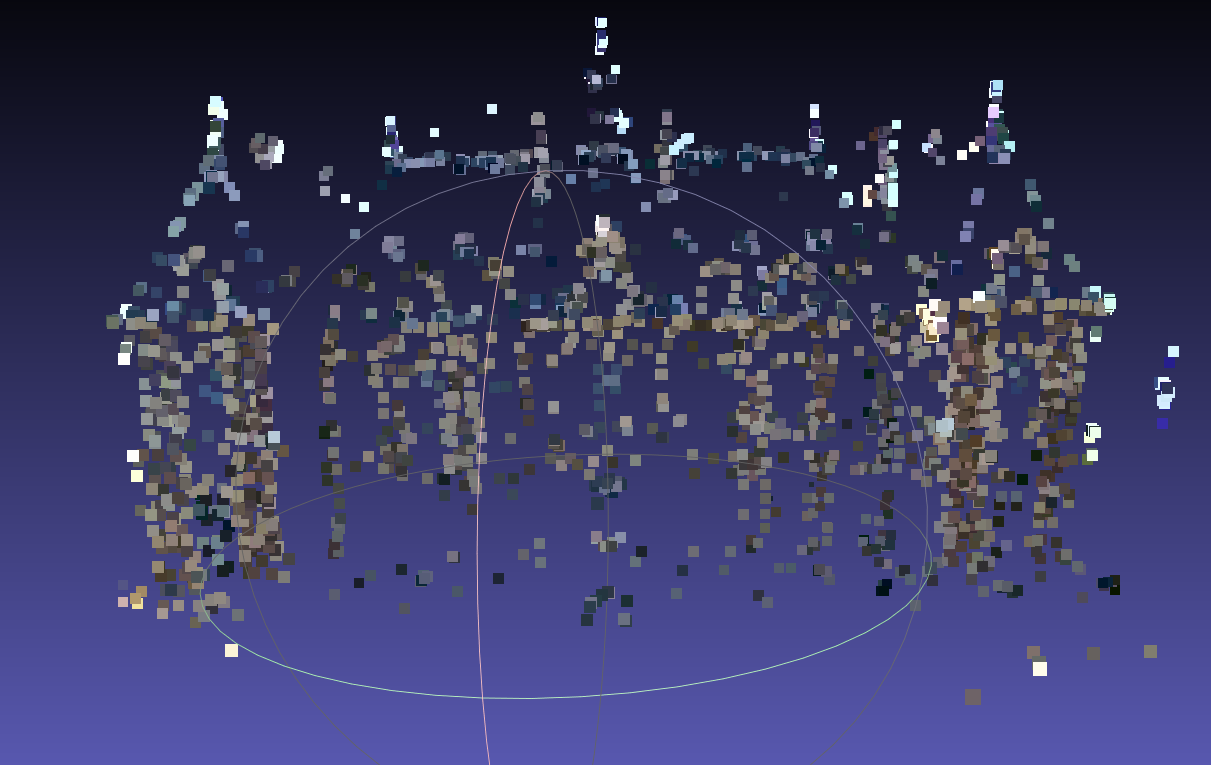
最终效果:
特别提醒:用 meshlab 打开后记得在右侧的设置框中将 shading 改为None !!!这样才能看到真正的颜色,也可以把点调大一点好看些