课程地址和说明
线性代数实现p4
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
本节是第五篇,由于CSDN限制,只能被迫拆分
矩阵计算
多元函数的等高线
此处参考视频:熟肉)多元微积分1.5,多元函数,等高线图——3Blue1Brown频道创始人 Grant 主讲,搬自可汗学院。 【自制中文字幕】
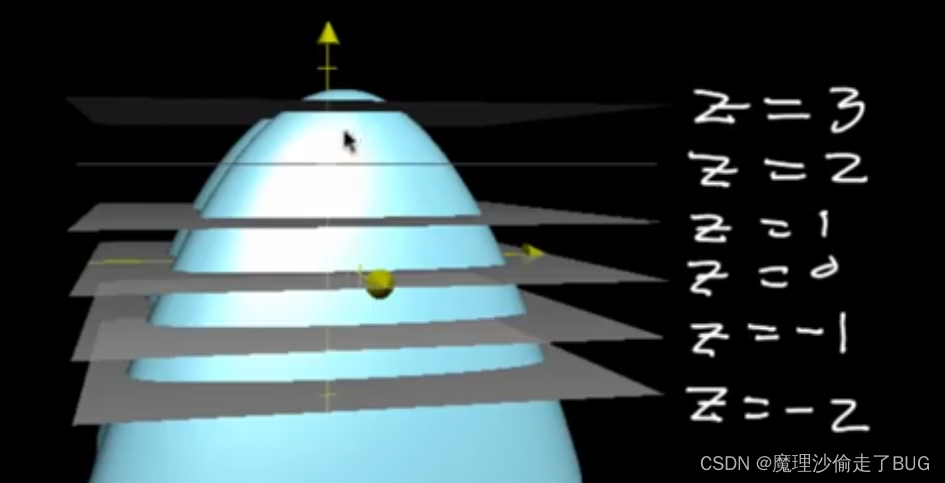
假设在三维坐标系中有这样一个多元函数构成的曲面:

我用平行于xOy平面的平面把这个曲面横着”切开“,曲面在不同平面上的投影的曲线投影到xOy平面上就成了等高线。



梯度(Gradient)
梯度向量的定义
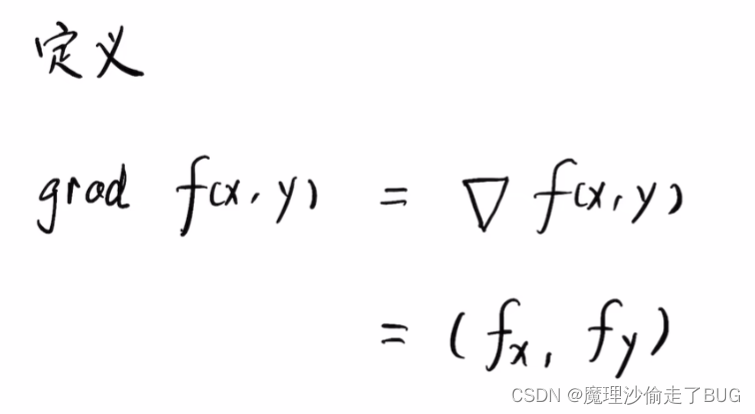
梯度向量的方向是方向导数(变化率)最大的方向
【提前注释一下】刚才提到的方向导数的公式为
∂
z
∂
l
→
=
f
x
(
x
0
,
y
0
)
c
o
s
α
+
f
y
(
x
0
,
y
0
)
c
o
s
β
=
(
f
x
(
x
0
,
y
0
)
,
f
y
(
x
0
,
y
0
)
)
⋅
(
c
o
s
α
,
c
o
s
β
)
,
这里写成了向量做内积的形式
=
▽
f
⋅
l
0
→
\frac{\partial z}{\partial\overrightarrow l}\\ =f_{x}(x_{0},y_{0})cos{\alpha}+f_{y}(x_{0},y_{0})cos{\beta}\\=(f_{x}(x_{0},y_{0}),f_{y}(x_{0},y_{0}))\cdot (cos{\alpha},cos{\beta}),这里写成了向量做内积的形式 \\=\bigtriangledown f\cdot \overrightarrow {l_{0}}
∂l∂z=fx(x0,y0)cosα+fy(x0,y0)cosβ=(fx(x0,y0),fy(x0,y0))⋅(cosα,cosβ),这里写成了向量做内积的形式=▽f⋅l0
其中
α
\alpha
α是向量
l
→
\overrightarrow l
l与
x
x
x轴(横轴)的夹角,
β
\beta
β是向量
l
→
\overrightarrow l
l与
y
y
y轴(纵轴)的夹角,
l
0
→
\overrightarrow {l_{0}}
l0是向量
l
→
\overrightarrow {l}
l单位化后的结果。

通过计算即可得出此结论,即梯度向量永远指向方向导数变化最大的方向。
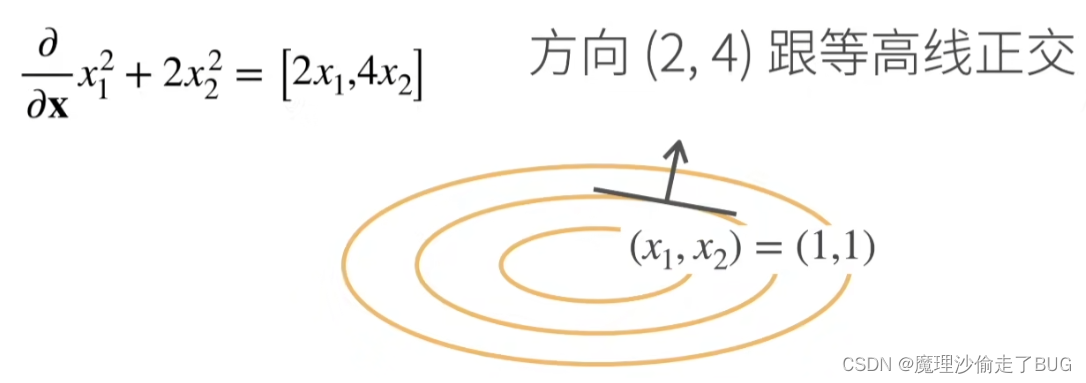
梯度向量的方向是与多元函数曲面对应等高线正交(垂直)
令
x
1
=
x
,
x
2
=
y
x_{1}=x,x_{2}=y
x1=x,x2=y,则上面李沐老师讲的这一块是想说明曲面
f
(
x
,
y
)
=
x
2
+
2
y
2
f(x,y)=x^{2}+2y^{2}
f(x,y)=x2+2y2在xOy平面上对应的等高线与梯度向量方向正交,而且梯度向量的方向是该函数变化率最大的方向。
P.S
终于把这篇看完了,对于我这个考考研数学二的学生来说,这篇太难懂了,查了大量资料,用了很长一段时间才看完,估计下面的章节还会有挑战,慢慢看吧




![[极客大挑战 2019]RCE ME 取反绕过正则匹配 绕过disable_function设置](https://img-blog.csdnimg.cn/0ec4f5eb8a4e4d698e6aab117546840d.png)