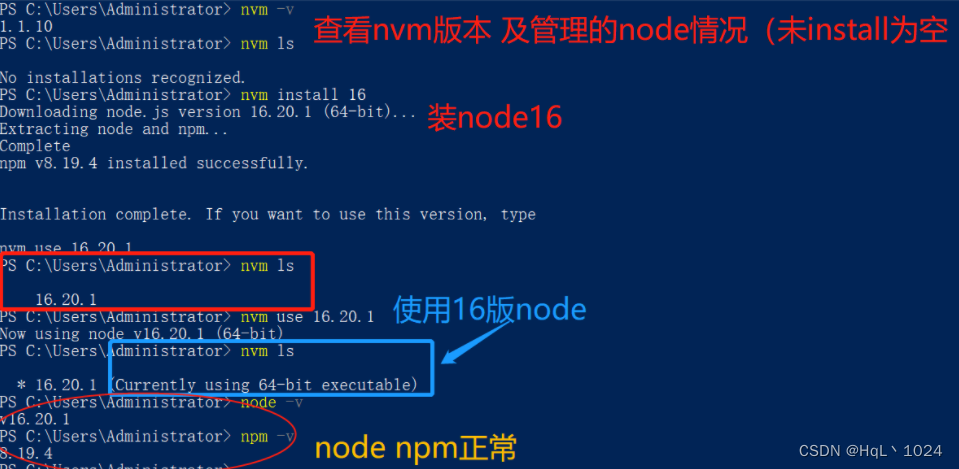
位运算理解:
n >> k:代表n右移k位 比如 000011 >> 1 = 000001 前面会补零(所以第几位是从0开始计算)
n & 1:表示最后一位是否为1
比如:n = 3 = 0011 而 1 = 0001 则3 & 1 = 0011 & 0001 为0001可以用来判断最后一位是否为1
lowbit操作,树状数组的基本操作:
lowbit(x)作用是返回x的最后一位1 最右边的一位1。
返回的是一个二进制数,返回最高位的一位1就是最后一位1
例如:x=1010,lowbit(x)=10;
x=101000,lowbit(x)=1000。
lowbot实现:
就是 x & -x,那么它为什么能返回最后一位1呢?
C++中一个数的负数是原码的补码(取反+1), -x = ~x + 1(负数x是在其负数补码基础上加1)
比如 这里1是最后一位1
原码 x = 1010…100…0
取反后这个0是最后一位0
反码 ~x = 0101…011…1
取反+1 到红色最后一位1以后,不会再往前进位
~x + 1 = 0101…100…0
取到了最后一位1
-x & ~x + 1 = 0000…100......0

原码、反码、补码
对于一个数,计算机要使用一定的编码方式进行二进制存储,二进制存储是计算机存储的本质。
原码、反码、补码是机器存储一个具体数字的编码方式,计算机是以二进制补码的形式进行数据的存储。
原码
原码就是符号位加上真值的绝对值,即用最高位表示符号,其余位表示值。比如如果是8位二进制:
- [+1] (原码) =
0000 0001 最高位为0,表示正数 - [ -1] (原码) =
1000 0001 最高位为1,表示负数
反码
反码表示方式是用来处理负数的,正数的反码是其本身,负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
- [+1] = [
00000001] (原码) = [00000001] (反码) - [ -1] = [
10000001] (原码) = [11111110] (反码)
补码
补码的表示方法是:正数的补码就是其本身,负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1(即在反码的基础上+1)
- [+1] = [
00000001] (原码) = [00000001] (反码) = [00000001] (补码) - [ -1] = [
10000001] (原码) = [11111110] (反码) = [11111111] (补码)
位运算最常用的两种操作:
1.求整数n二进制表示中第k位(从个位开始算)数字是几:n >> k & 1
- 先把第k位数字移到最后一位 n >> k
- 再看一下个位是几 x & 1
从最高位右移,再与1做与运算,输出二进制表示
int main()
{
int n = 10;
for(int k = 3; k >= 0; k --) cout << (n >> k & 1);
return 0;
}
结果:1010

- 求一个 数二进制中1的个数:
- 在我们的机器上,int数据类型是32位;
- 因此,我们将1从最低位一直移动到最高位,并将每一位与输出的数值a 做 与运算
- 如果a对应位是1,则将计数器 cnt+1,最终 cnt 就是该整数二进制数中1的个数。
#include <iostream>
using namespace std;
int lowbit(int x)
{
return x & -x;
}
int main()
{
int n;
cin >> n;
while(n --){
int x;
cin >> x;
int res = 0;
// 每次减去x的最后一位1
while(x) x -= lowbit(x), res ++;
cout << res << ' ';
}
return 0;
}