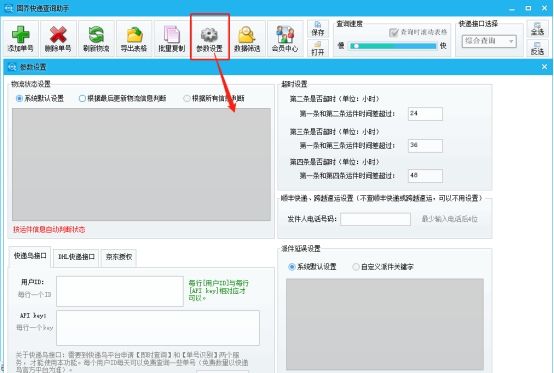
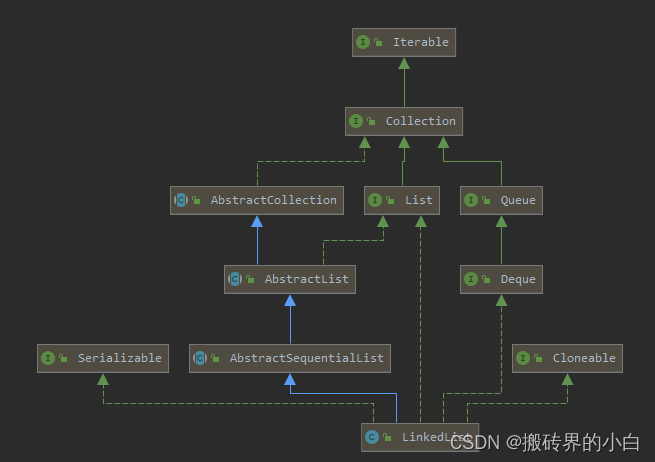
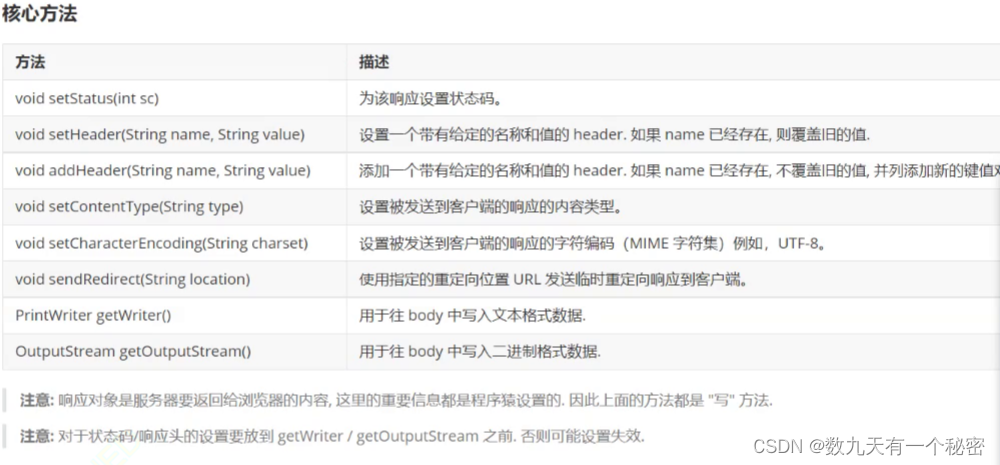
思路：使用一个小根堆+一个大根堆来找中位数

小根堆保存较大的一半数字，大根堆保存较小的一半数字

奇数queMin的队头即为中位数，偶数queMin和queMax队头相加/2为中位数

初始状态： queMin: [] queMax: []

1. 添加数字 1： queMin: [1] queMax: [] 中位数1

2. 添加数字 2： queMin: [2] queMax: [1] 中位数1.5

3. 添加数字 3： queMin: [2, 3] queMax: [1] 中位数2

4. 添加数字 4： queMin: [3, 4] queMax: [2, 1] 中位数 2.5

5. 添加数字 5： queMin: [3, 4, 5] queMax: [2, 1] 中位数3

6. 添加数字 3.5： queMin: [3, 4, 5] queMax: [3.5, 1, 2] 中位数 3.25

class MedianFinder {
    PriorityQueue<Integer> queMin = new PriorityQueue<>();
    PriorityQueue<Integer> queMax = new PriorityQueue<>((a,b)->b-a);
    public MedianFinder() {
    }
    
    public void addNum(int num) {
        if(queMin.isEmpty()||num>queMin.peek()){
            queMin.add(num);
            if(queMin.size()-queMax.size()>1){
                queMax.add(queMin.poll());
            }
        }else{
            queMax.add(num);
            if (queMax.size() > queMin.size()) {
                queMin.offer(queMax.poll());
            }
        }
    }
    
    public double findMedian() {
        if(queMin.size()>queMax.size()){
            return queMin.peek();
        }
        else{
            return (queMin.peek()+queMax.peek())/2.0;
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */