深度学习——线性神经网络二
文章目录
- 前言
- 一、softmax回归
- 1.1. 分类问题
- 1.2. 网络架构
- 1.3. 全连接层的参数开销
- 1.4. softmax运算
- 1.5. 小批量样本的向量化
- 1.6. 损失函数
- 1.6.1. 对数似然
- 1.6.2. softmax及其导数
- 1.6.3. 交叉熵损失
- 1.7. 信息论基础
- 1.7.1 熵
- 1.7.2. 信息量
- 1.7.3. 重新审视交叉熵
- 1.8. 模型预测和评估
- 二、图像分类数据集
- 2.1.读取数据集
- 2.2. 读取小批量
- 2.3. 整合所有组件
- 总结
前言
书接上章,继续线性神经网络的学习,本章将主要讲softmax回归
参考书:
《动手学深度学习》
一、softmax回归
softmax回归是一种多分类模型,也称为多项的Logistic回归,是Logistic回归在多分类问题上的推广。它可以将输入向量映射为一个概率分布,用于预测属于每个类别的概率。
1.1. 分类问题
我们从一个图像分类问题开始。 假设每次输入是一个2×2的灰度图像。
我们可以用一个标量表示每个像素值,每个图像对应四个特征x1,x2,x3,x4。 此外,假设每个图像属于类别“猫”“鸡”和“狗”中的一个。
接下来,我们要选择如何表示标签。 我们有两个明显的选择:
- 最直接的想法是选择y∈{1,2,3}, 其中整数分别代表{狗,猫,鸡}。
- 如果类别间有一些自然顺序, 比如说我们试图预测{婴儿,儿童,青少年,青年人,中年人,老年人}, 那么将这个问题转变为回归问题,并且保留这种格式是有意义的。
统计学家很早以前就发明了一种表示分类数据的简单方法:独热编码。 独热编码是一个向量,它的分量和类别一样多。
类别对应的分量设置为1,其他所有分量设置为0。
在我们的例子中,标签y将是一个三维向量, 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”:
y∈{(1,0,0),(0,1,0),(0,0,1)}.
1.2. 网络架构
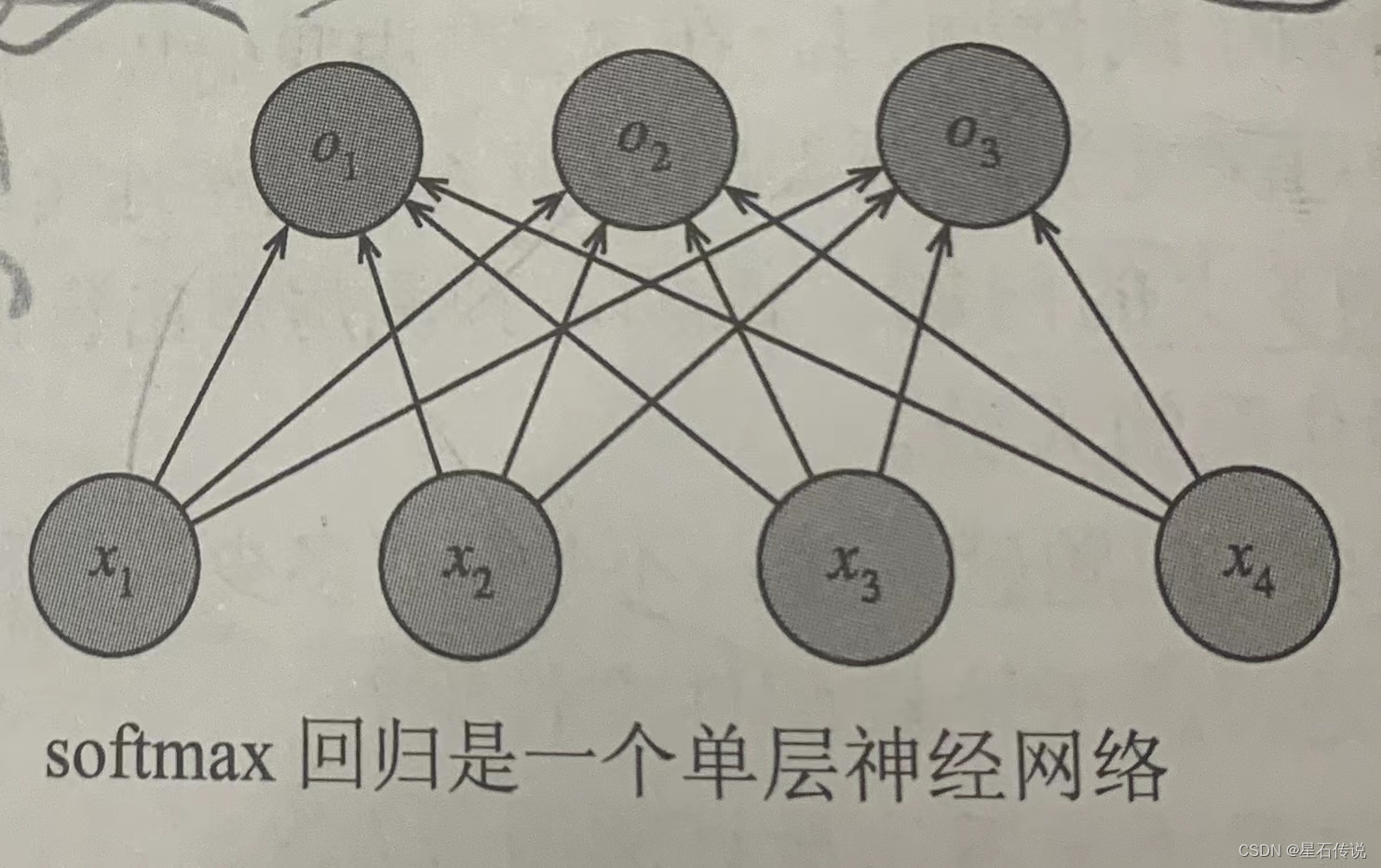
在我们的例子中,由于我们有4个特征和3个可能的输出类别, 我们将需要12个标量来表示权重(带下标的w), 3个标量来表示偏置(带下标的b)。 下面我们为每个输入计算三个未规范化的预测(logit):o1、o2和o3。
o
1
=
x
1
w
11
+
x
2
w
12
+
x
3
w
13
+
x
4
w
14
+
b
1
,
o
2
=
x
1
w
21
+
x
2
w
22
+
x
3
w
23
+
x
4
w
24
+
b
2
,
o
3
=
x
1
w
31
+
x
2
w
32
+
x
3
w
33
+
x
4
w
34
+
b
3
.
\begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\\ o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\\ o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3. \end{aligned}
o1o2o3=x1w11+x2w12+x3w13+x4w14+b1,=x1w21+x2w22+x3w23+x4w24+b2,=x1w31+x2w32+x3w33+x4w34+b3.
如图所示:
为了更简洁地表达模型,我们仍然使用线性代数符号。
通过向量形式表达为
o
=
W
x
+
b
\mathbf{o} = \mathbf{W} \mathbf{x} + \mathbf{b}
o=Wx+b,
由此,我们已经将所有权重放到一个 3 × 4 3 \times 4 3×4矩阵中。 对于给定数据样本的特征 x \mathbf{x} x,
我们的输出是由权重与输入特征进行矩阵-向量乘法再加上偏置 b \mathbf{b} b得到的。
1.3. 全连接层的参数开销
在深度学习中,全连接层无处不在。 全连接层是“完全”连接的,可能有很多可学习的参数。
具体来说,对于任何具有
d
d
d个输入和
q
q
q个输出的全连接层,
参数开销为
O
(
d
q
)
\mathcal{O}(dq)
O(dq),这个数字在实践中可能高得令人望而却步。
幸运的是,将
d
d
d个输入转换为
q
q
q个输出的成本可以减少到
O
(
d
q
n
)
\mathcal{O}(\frac{dq}{n})
O(ndq),
其中超参数
n
n
n可以由我们灵活指定,以在实际应用中平衡参数节约和模型有效性
1.4. softmax运算
现在我们将优化参数以最大化观测数据的概率。
为了得到预测结果,我们将设置一个阈值,如选择具有最大概率的标签。
我们希望模型的输出 y ^ j \hat{y}_j y^j可以视为属于类 j j j的概率,然后选择具有最大输出值的类别 argmax j y j \operatorname*{argmax}_j y_j argmaxjyj作为我们的预测。
例如,如果 y ^ 1 \hat{y}_1 y^1、 y ^ 2 \hat{y}_2 y^2和 y ^ 3 \hat{y}_3 y^3分别为0.1、0.8和0.1
那么我们预测的类别是2,在我们的例子中代表“鸡”。
但我们不能将未规范化的预测 o o o直接视作我们感兴趣的输出
因为将线性层的输出直接视为概率时存在一些问题:
一方面,我们没有限制这些输出数字的总和为1。
另一方面,根据输入的不同,它们可以为负值。
要将输出视为概率,我们必须保证在任何数据上的输出都是非负的且总和为1。
softmax函数能够将未规范化的预测变换为非负数并且总和为1,同时让模型保持可导的性质。
为了完成这一目标,我们首先对每个未规范化的预测求幂,这样可以确保输出非负。
为了确保最终输出的概率值总和为1,我们再让每个求幂后的结果除以它们的总和。如下式:
y ^ = s o f t m a x ( o ) 其中 y ^ j = exp ( o j ) ∑ k exp ( o k ) \hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)} y^=softmax(o)其中y^j=∑kexp(ok)exp(oj)
softmax运算不会改变未规范化的预测
o
\mathbf{o}
o之间的大小次序,只会确定分配给每个类别的概率。
因此,在预测过程中,我们仍然可以用下式来选择最有可能的类别。
argmax j y ^ j = argmax j o j . \operatorname*{argmax}_j \hat y_j = \operatorname*{argmax}_j o_j. jargmaxy^j=jargmaxoj.
尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。因此,softmax回归是一个线性模型。
1.5. 小批量样本的向量化
为了提高计算效率并且充分利用GPU,我们通常会对小批量样本的数据执行向量计算。
假设我们读取了一个批量的样本
X
\mathbf{X}
X,
其中特征维度(输入数量)为
d
d
d,批量大小为
n
n
n。
此外,假设我们在输出中有
q
q
q个类别。
那么小批量样本的特征为
X
∈
R
n
×
d
\mathbf{X} \in \mathbb{R}^{n \times d}
X∈Rn×d,权重为
W
∈
R
d
×
q
\mathbf{W} \in \mathbb{R}^{d \times q}
W∈Rd×q,偏置为
b
∈
R
1
×
q
\mathbf{b} \in \mathbb{R}^{1\times q}
b∈R1×q。
softmax回归的向量计算表达式为:
O = X W + b , Y ^ = s o f t m a x ( O ) . \begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \\ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}). \end{aligned} OY^=XW+b,=softmax(O).
小批量样本的向量化加快了 X 和 W \mathbf{X}和\mathbf{W} X和W的矩阵-向量乘法。
对于 O \mathbf{O} O的每一行,我们先对所有项进行幂运算,然后通过求和对它们进行标准化。 X W + b \mathbf{X} \mathbf{W} + \mathbf{b} XW+b的求和会使用广播机制,
小批量的未规范化预测 O \mathbf{O} O和输出概率 Y ^ \hat{\mathbf{Y}} Y^都是形状为 n × q n \times q n×q的矩阵。
1.6. 损失函数
我们需要一个损失函数来度量预测的效果。我们将使用最大似然估计,这与在线性回归中的方法相同。
1.6.1. 对数似然
softmax函数给出了一个向量
y
^
\hat{\mathbf{y}}
y^,
我们可以将其视为“对给定任意输入
x
\mathbf{x}
x的每个类的条件概率”。
例如,
y
^
1
\hat{y}_1
y^1=
P
(
y
=
猫
∣
x
)
P(y=\text{猫} \mid \mathbf{x})
P(y=猫∣x)。
假设整个数据集
{
X
,
Y
}
\{\mathbf{X}, \mathbf{Y}\}
{X,Y}具有
n
n
n个样本,
其中索引
i
i
i的样本由特征向量
x
(
i
)
\mathbf{x}^{(i)}
x(i)和独热标签向量
y
(
i
)
\mathbf{y}^{(i)}
y(i)组成。
我们可以将估计值与实际值进行比较:
P ( Y ∣ X ) = ∏ i = 1 n P ( y ( i ) ∣ x ( i ) ) . P(\mathbf{Y} \mid \mathbf{X}) = \prod_{i=1}^n P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}). P(Y∣X)=i=1∏nP(y(i)∣x(i)).
根据最大似然估计,我们最大化 P ( Y ∣ X ) P(\mathbf{Y} \mid \mathbf{X}) P(Y∣X),相当于最小化负对数似然:
− log P ( Y ∣ X ) = ∑ i = 1 n − log P ( y ( i ) ∣ x ( i ) ) = ∑ i = 1 n l ( y ( i ) , y ^ ( i ) ) , -\log P(\mathbf{Y} \mid \mathbf{X}) = \sum_{i=1}^n -\log P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}) = \sum_{i=1}^n l(\mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)}), −logP(Y∣X)=i=1∑n−logP(y(i)∣x(i))=i=1∑nl(y(i),y^(i)),
其中,对于任何标签 y \mathbf{y} y和模型预测 y ^ \hat{\mathbf{y}} y^,损失函数为:
l ( y , y ^ ) = − ∑ j = 1 q y j log y ^ j . l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j. l(y,y^)=−j=1∑qyjlogy^j.
通常被称为交叉熵损失(cross-entropy loss)。
由于
y
\mathbf{y}
y是一个长度为
q
q
q的独热编码向量,
所以除了一个项以外的所有项
j
j
j都消失了。
由于所有
y
^
j
\hat{y}_j
y^j都是预测的概率,所以它们的对数永远不会大于
0
0
0。
因此,如果正确地预测实际标签,即如果实际标签
P
(
y
∣
x
)
=
1
P(\mathbf{y} \mid \mathbf{x})=1
P(y∣x)=1,
则损失函数不能进一步最小化。
注意,这往往是不可能的。
例如,数据集中可能存在标签噪声(比如某些样本可能被误标),
或输入特征没有足够的信息来完美地对每一个样本分类。
1.6.2. softmax及其导数
利用softmax的定义,我们代入得到:
l ( y , y ^ ) = − ∑ j = 1 q y j log exp ( o j ) ∑ k = 1 q exp ( o k ) = ∑ j = 1 q y j log ∑ k = 1 q exp ( o k ) − ∑ j = 1 q y j o j = log ∑ k = 1 q exp ( o k ) − ∑ j = 1 q y j o j . \begin{aligned} l(\mathbf{y}, \hat{\mathbf{y}}) &= - \sum_{j=1}^q y_j \log \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} \\ &= \sum_{j=1}^q y_j \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j\\ &= \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j. \end{aligned} l(y,y^)=−j=1∑qyjlog∑k=1qexp(ok)exp(oj)=j=1∑qyjlogk=1∑qexp(ok)−j=1∑qyjoj=logk=1∑qexp(ok)−j=1∑qyjoj.
考虑相对于任何未规范化的预测 o j o_j oj的导数,我们得到:
∂ o j l ( y , y ^ ) = exp ( o j ) ∑ k = 1 q exp ( o k ) − y j = s o f t m a x ( o ) j − y j . \partial_{o_j} l(\mathbf{y}, \hat{\mathbf{y}}) = \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} - y_j = \mathrm{softmax}(\mathbf{o})_j - y_j. ∂ojl(y,y^)=∑k=1qexp(ok)exp(oj)−yj=softmax(o)j−yj.
换句话说,导数是我们softmax模型分配的概率与实际发生的情况(由独热标签向量表示)之间的差异。
从这个意义上讲,这与我们在回归中看到的非常相似, 其中梯度是观测值 y y y和估计值 y ^ \hat{y} y^之间的差异。
这不是巧合,在任何指数族分布模型中,对数似然的梯度正是由此得出的。
1.6.3. 交叉熵损失
对于标签 y \mathbf{y} y,我们可以使用与以前相同的表示形式。唯一的区别是,我们现在用一个概率向量表示,如 ( 0.1 , 0.2 , 0.7 ) (0.1, 0.2, 0.7) (0.1,0.2,0.7),而不是仅包含二元项的向量 ( 0 , 0 , 1 ) (0, 0, 1) (0,0,1)。
我们使用
l
(
y
,
y
^
)
=
−
∑
j
=
1
q
y
j
log
y
^
j
.
l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j.
l(y,y^)=−j=1∑qyjlogy^j.来定义损失
l
l
l,它是所有标签分布的预期损失值。
此损失称为交叉熵损失(cross-entropy loss),它是分类问题最常用的损失之一。
1.7. 信息论基础
信息论(information theory)涉及编码、解码、发送以及尽可能简洁地处理信息或数据。
1.7.1 熵
信息论的核心思想是量化数据中的信息内容。
在信息论中,该数值被称为分布
P
P
P的熵(entropy)。可以通过以下方程得到:
H [ P ] = ∑ j − P ( j ) log P ( j ) . H[P] = \sum_j - P(j) \log P(j). H[P]=j∑−P(j)logP(j).
1.7.2. 信息量
压缩与预测有什么关系呢? 想象一下,我们有一个要压缩的数据流。 如果我们很容易预测下一个数据,那么这个数据就很容易压缩。 为什么呢?
举一个极端的例子,假如数据流中的每个数据完全相同,这会是一个非常无聊的数据流。 由于它们总是相同的,我们总是知道下一个数据是什么。
所以,为了传递数据流的内容,我们不必传输任何信息。也就是说,“下一个数据是xx”这个事件毫无信息量。
但是,如果我们不能完全预测每一个事件,那么我们有时可能会感到"惊异"。
克劳德·香农决定用信息量
log
1
P
(
j
)
=
−
log
P
(
j
)
\log \frac{1}{P(j)} = -\log P(j)
logP(j)1=−logP(j)来量化这种惊异程度。
在观察一个事件
j
j
j时,并赋予它(主观)概率
P
(
j
)
P(j)
P(j)。
当我们赋予一个事件较低的概率时,我们的惊异会更大,该事件的信息量也就更大。
熵是当分配的概率真正匹配数据生成过程时的信息量的期望。
1.7.3. 重新审视交叉熵
可以把熵 H ( P ) H(P) H(P)想象为“知道真实概率的人所经历的惊异程度”,
交叉熵从
P
P
P到
Q
Q
Q,记为
H
(
P
,
Q
)
H(P, Q)
H(P,Q)。
我们可以把交叉熵想象为“主观概率为
Q
Q
Q的观察者在看到根据概率
P
P
P生成的数据时的预期惊异”。
当
P
=
Q
P=Q
P=Q时,交叉熵达到最低。
在这种情况下,从
P
P
P到
Q
Q
Q的交叉熵是
H
(
P
,
P
)
=
H
(
P
)
H(P, P)= H(P)
H(P,P)=H(P)。
简而言之,我们可以从两方面来考虑交叉熵分类目标:
- 最大化观测数据的似然
- 最小化传达标签所需的惊异。
1.8. 模型预测和评估
在训练softmax回归模型后,给出任何样本特征,我们可以预测每个输出类别的概率。
通常我们使用预测概率最高的类别作为输出类别。如果预测与实际类别(标签)一致,则预测是正确的。我们将使用精度(accuracy)来评估模型的性能。
精度等于正确预测数与预测总数之间的比率。
二、图像分类数据集
2.1.读取数据集
通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中,转换过程将图像从原始的图片格式(如JPEG、PNG等)转化为数字格式,以便于在计算机中进行处理和分析。
如果你第一次运行代码时尚未下载数据集,它会自动进行下载。如果你之后再次运行代码,它不会重新下载数据集,而是直接加载已经下载好的数据集。这样可以避免重复下载相同的数据集。
#图像分类数据集:
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式,并除以255使得所有像素的数值均在0~1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root= "../data",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
print(len(mnist_train), len(mnist_test))
print(mnist_train[0][0].shape)
#结果:
60000 10000
torch.Size([1, 28, 28])
每个输入图像的高度和宽度均为28像素。 数据集由灰度图像组成,其通道数为1。
Fashion-MNIST中包含的10个类别, 以下函数用于在数字标签索引及其文本名称之间进行转换:
def get_fashion_mnist_labels(labels):
#返回Fashion-MNIBT数据集的文本标签
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
#创建一个函数来可视化这些样本。
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save
"""绘制图像列表"""
figsize = (num_cols * scale, num_rows * scale)
_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
axes = axes.flatten()
for i, (ax, img) in enumerate(zip(axes, imgs)):
if torch.is_tensor(img):
# 图片张量
ax.imshow(img.numpy())
else:
# PIL图片
ax.imshow(img)
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
if titles:
ax.set_title(titles[i])
return axes
#以下是训练数据集中前几个样本的图像及其相应的标签
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y))
d2l.plt.show()

2.2. 读取小批量
为了使我们在读取训练集和测试集时更容易,我们使用内置的数据迭代器,而不是从零开始创建。
通过内置数据迭代器,我们可以随机打乱了所有样本,从而无偏见地读取小批量。
batch_size = 256
def get_dataloader_workers(): #@save
"""使用4个进程来读取数据"""
return 4
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers())
#看一下读取训练数据所需的时间
timer = d2l.Timer()
for X, y in train_iter:
continue
print(f'{timer.stop():.2f} sec')
#结果:
4.31 sec
2.3. 整合所有组件
现在我们定义load_data_fashion_mnist函数,
用于获取和读取Fashion-MNIST数据集。 这个函数返回训练集和验证集的数据迭代器。 此外,这个函数还接受一个可选参数resize,用来将图像大小调整为另一种形状。
def load_data_fashion_mnist(batch_size, resize=None): #@save
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers()),
data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=get_dataloader_workers()))
#通过指定resize参数来测试load_data_fashion_mnist函数的图像大小调整功能。
train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
print(X.shape, X.dtype, y.shape, y.dtype)
break
#结果”
torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64
#X.shape:代表它的每个批次包含32个样本。每个样本的形状是(1, 64, 64),像素由原来的28变为了64
我们现在已经准备好使用Fashion-MNIST数据集,便于之后调用来评估各种分类算法。
总结
本章讲述了softmax回归的原理,并且下载好了Fashion-MNIST数据集便于后续分析使用。
是以圣人之治,虛其心,實其腹,弱其志,強其骨。常使民無知
–2023-9-19 进阶篇