数据结构与算法(C语言版)P5---栈

news2024/9/29 7:32:31

1、栈

1.1、栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。__进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。__栈中的数据元素遵守__后进先出（先进后出）__LIFO（Last In First Out）的原则。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。

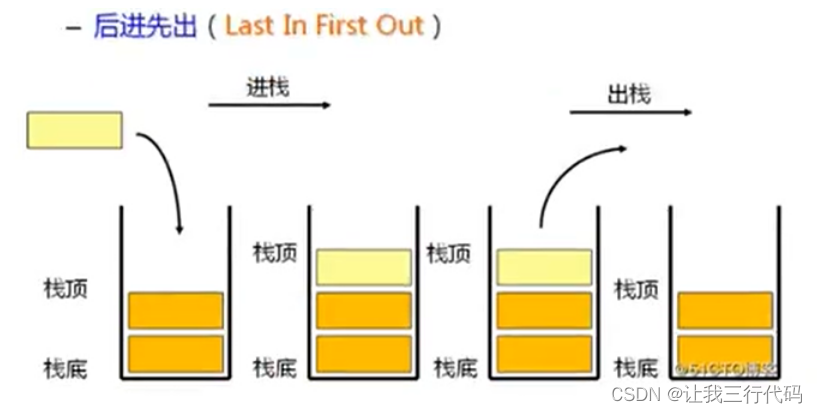
在这里插入图片描述

栈（stack）是一种特殊的线性表，是限定仅在一端（通常是表尾）进行插入和删除操作的线性表。

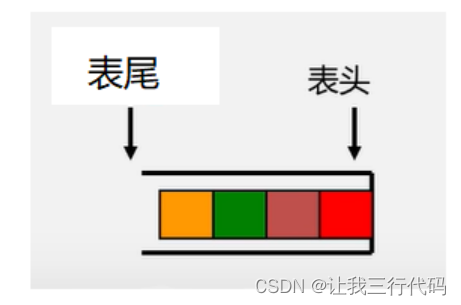
在这里插入图片描述

栈是仅在表尾进行插入、删除操作的线性表。

表尾（即an端）称为栈顶Top；表头（即a1端）称为栈底Base。

例如：

栈 S = (a1,a2,a3…an)

总结：表尾对应栈顶，表头对应栈底。

栈有两种：数组栈，链表栈。

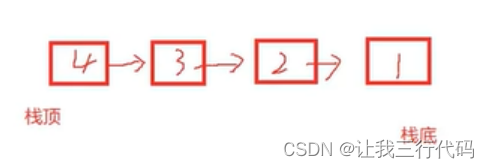
在这里插入图片描述

在这里插入图片描述

链式栈：

  • 如果是用尾做栈顶，尾插尾删，要设计成双向链表，否则删除数据效率低。
  • 如果是用头做栈顶，头插头删，要设计成单向链表。

两种都可以，非要选一种，数组栈结构稍微好一点。

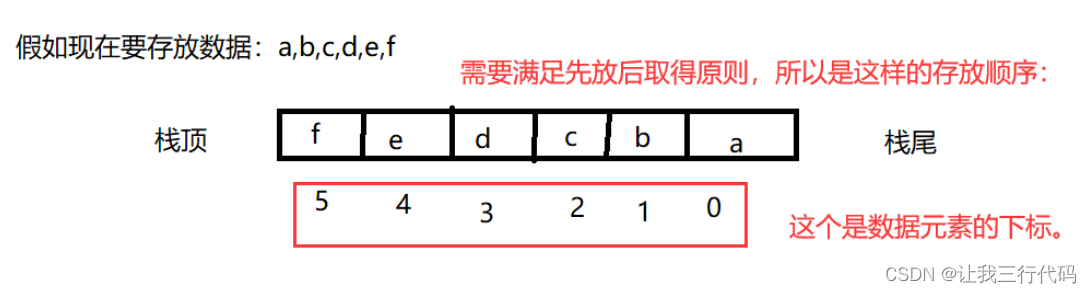
数组栈存放数据的方式：

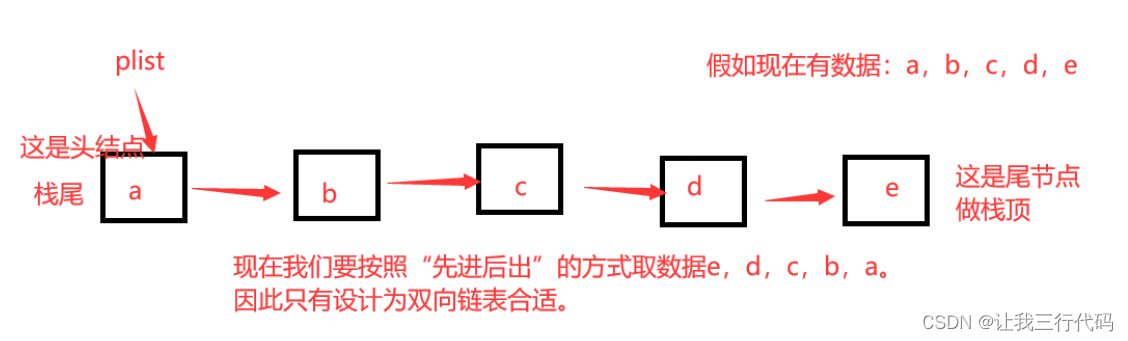
在这里插入图片描述

链式栈存放数据的方式：

  • 尾做栈顶：

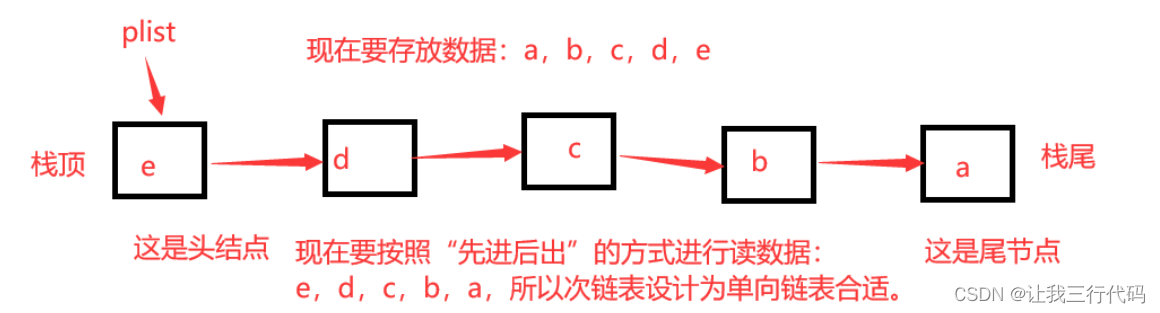
    在这里插入图片描述

  • 头做栈顶

    在这里插入图片描述

总结：栈和队列时线性表的子集，是插入金额删除位置受限的线性表。

1.2、栈的思考题

问：假设与3个元素a，b，c。入栈顺序是a，b，c。

则它们的出栈出栈顺序有几种可能？

答案：5种可能。下面解释：

（1）c、b、a。原因：入栈顺序为a、b、c，然后依次取出。

（2）a、b、c。原因：a先入栈，然后出栈，之后b入栈，b出栈，最后c入栈，c出栈。

（3）a、c、b。原因：a先入栈，然后出栈，之后b、c入栈，最后，c、b出栈。

（4）b、a、c。原因：a、b先入栈，之后b、a出栈，最后c入栈，c出栈。

（5）b、c、a。原因：a、b先入栈，之后b出栈，然后c入栈，最后c、a出栈。

2、顺序栈的实现（用数组实现）

栈主要有以下几个接口函数

  • 初始化栈（StackInit）
  • 销毁（StackDestroy）
  • 栈顶插入数据（StackPush）
  • 栈顶删除数据（StackPop）
  • 取栈顶数据（StackTop）
  • 统计栈种元素个数（StackSize）
  • 判断栈是否为空（StackEmpty）

2.1、定义结构体和main函数

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int SLDataType;

typedef struct Stack
{
	SLDataType* a;
	int top;        //栈顶
	int capacity;
};

main函数

#include "stack.h"

int main()
{
	ST st;
	return 0;
}

2.2、初始化栈

//初始化栈
void StackInit(ST* ps)
{
	assert(ps);

	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

2.3、销毁

//销毁
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

2.4、栈顶插入数据

//栈顶插入数据
void StackPush(ST* ps, SLDataType x)
{
	assert(ps);

	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * newcapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}

2.5、栈顶删除数据

//栈顶删除数据
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}

2.6、取栈顶元素

//取栈顶数据
SLDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top - 1];
}

2.7、统计栈中元素个数

//统计栈中元素个数
int StackSize(ST* ps)
{
	return ps->top;
}

2.8、判断栈是否为空

//判断栈是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

3、全代码展示

这里使用三个文件：

  • stack.h：用于结构体、各种函数接口的声明
  • stack.c：用于各种函数接口的定义。
  • test.c：用于创建链表，实现链表。

3.1、stack.h

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;        //栈顶
	int capacity;
}ST;

void StackInit(ST* ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);        //取栈顶的数据
int StackSize(ST* ps);       //统计栈里面有多少个数据
bool StackEmpty(ST* ps);

3.2、stack.c

#include "stack.h"

void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	//初始化时，top给的是0，意味着top指向栈顶数据的下一个。
	//初始化时，top给的是-1，意味着top指向栈顶数据。
	ps->top = 0;
	ps->capacity = 0;
}
void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;

}
void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = realloc(ps->a, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
//删除数据
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}

STDataType StackTop(ST* ps)   //取栈顶的数据
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top-1];
}

int StackSize(ST* ps)       //统计栈里面有多少个数据
{
	return ps->top;
}

bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

3.3、test.c

#include "stack.h"

void TestStack()
{
	ST st;
	StackInit(&st);
	StackPush(&st, 1);
	StackPush(&st, 2);
	StackPush(&st, 3);
	StackPush(&st, 4);
	StackPush(&st, 5);
	StackPush(&st, 6);

	//遍历栈元素
	while (!StackEmpty(&st))
	{
		printf("%d ", StackTop(&st)); 
		StackPop(&st);
	}

	StackDestroy(&st);
}

int main()
{
	TestStack();
	return 0;
}

4、链栈的实现（用链表实现栈）

链栈的实现（用链表实现栈）

前面说过链栈的实现有两种方式：

  • 链表头做栈顶，这样只需要单链表即可。
  • 链表尾做栈顶，这样需要双向链表。

这里我们就以单链表的形式实现链表。

以单链表的形式实现链表，链表的结构如下：
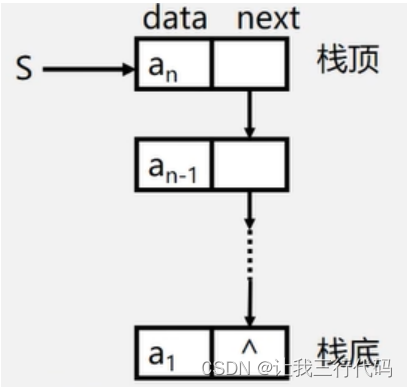
在这里插入图片描述

这个样的链表有如下特性：

  • 链表的头指针就是栈顶。
  • 不需要头结点。
  • 基本不存在栈满的情况（需要结点就立即申请即可）。
  • 空栈相当于头指针指向NULL。
  • 插入和删除仅在栈顶处执行。

栈主要是用数组实现，链栈稍微少一点，所以这里直接放全代码，不在一个接口一个接口的分析了。
以下是个人写的版本

4.1、stack.h

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int SLDataType;

typedef struct Stack
{
	struct Stack* Next; 
	SLDataType data;
}ST;


//销毁
void StackDestory(ST** pps);

//插入数据
void StackPush(ST** pps, SLDataType x);

//删除数据
void StackPop(ST** pps);

//取栈顶元素
SLDataType StackTop(ST** pps);

//统计栈里面有多少个数据
int StackSize(ST** pps);

//判断栈是否为空
bool StackEmpty(ST** pps);

4.2、stack.c

#include "stack.h"

//插入数据
void StackPush(ST** pps, SLDataType x)
{
	//先扩容
	ST* newnode = (ST*)malloc(sizeof(ST));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	newnode->data = x;
	newnode->Next = *pps;
	*pps = newnode;
}

//销毁
void StackDestory(ST** pps)
{
	ST* cur = *pps;
	while (cur)
	{
		ST* next = cur->Next; 
		free(cur);
		cur = next;
	}
	*pps = NULL;
}

//删除栈顶
void StackPop(ST** pps)
{
	assert(*pps != NULL);
	ST* next = (*pps)->Next;
	free(*pps);
	*pps = next;
}

//取栈顶元素
SLDataType StackTop(ST** pps)
{
	assert(*pps != NULL);
	return (*pps)->data;
}

//统计栈里面有多少个数据
int StackSize(ST** pps)
{
	assert(*pps != NULL);

	int count = 0;
	ST* cur = *pps;
	while (cur)
	{
		count++;
		cur = cur->Next;
	}
	return count;
}

//判断栈是否为空
bool StackEmpty(ST** pps)
{
	assert(pps);
	return *pps == NULL;
}

4.3、test.c

#include "stack.h"

int main()
{
	ST* st = NULL;

	StackPush(&st, 1);
	StackPush(&st, 2);
	StackPush(&st, 3);
	StackPush(&st, 4);
	StackPush(&st, 5);
	StackPush(&st, 7);

	
	ST** cur = &st;
	while (*cur)
	{
		st = *cur;
		printf("%d ", StackTop(&st));
		StackPop(&st);
	}

	StackDestory(&st);
	return 0;
}

5、栈与递归

递归的定义：

  • 若一个对象部分的包含它自己，或用它自己给自己定义，则称这个对象是递归的。
  • 若一个过程直接的或间接的调用自己，则称这个过程是递归的过程。

以下三种情况常常用到递归方法

  • 递归定义的数学函数。
    • 阶乘函数。
    • 斐波那契数列。
  • 具有递归特性的数据结构。
    • 二叉树。
    • 广义表。
  • 可递归求解的问题。
    • 迷宫问题。
    • Hanoi塔问题。

递归问题————使用分治法求解

__分治法：__对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解。

使用分治法的三个条件：

  • 能将一个问题转变为一个新问题，而新问题与原问题的解法相同或类同，不同的仅是处理的对象，且这些对象是变化有规律的。
  • 可以通过上述转化而使问题简化。
  • 必须有一个明确的递归出口，或称为递归边界。

我们再来分析函数递归掉调用过程：

调用前，系统完成：

  • 将实参，返回地址等传递给被调用函数。
  • 为被调用函数的局部变量分配存储区。
  • 将控制转移到被调用函数。

调用后，系统完成：

  • 保存被调用函数的计算结果。
  • 释放被调用函数的数据区。
  • 依照被调用函数保存的返回地址将控制转移到调用函数。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1025748.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【C++STL基础入门】list改、查操作

【C++STL基础入门】list改、查操作

文章目录 前言一、list查操作1.1 迭代器循环1.2 for_each函数 二、list改操作2.1 迭代器修改2.2 assign函数2.3 运算符 总结 前言 C标准模板库&#xff08;STL&#xff09;是C语言中非常重要的部分&#xff0c;它提供了一组通用的模板类和函数&#xff0c;用于处理常见的数据结…
阅读更多...
利用C++开发一个迷你的英文单词录入和测试小程序-源码

利用C++开发一个迷你的英文单词录入和测试小程序-源码

接上一篇&#xff0c;有了数据库的查询&#xff0c;再把小测试的功能给补足&#xff0c;小程序的结构就出来了。 备注&#xff1a;enable_if 有更优秀的concept C 20替代品&#xff0c;C11 里面提到的any&#xff0c;variant&#xff0c;再C17 已经被纳入了标准库。这里完全可…
阅读更多...
iOS加固保护技术：保护你的iOS应用免受恶意篡改

iOS加固保护技术：保护你的iOS应用免受恶意篡改

目录 转载&#xff1a;开始使用ipaguard 前言 下载ipa代码混淆保护工具 获取ipaguard登录码 代码混淆 文件混淆 IPA重签名与安装测试 转载&#xff1a;开始使用ipaguard 前言 iOS加固保护是直接针对ios ipa二进制文件的保护技术&#xff0c;可以对iOS APP中的可执行文件…
阅读更多...
机器学习（17）---支持向量机(SVM)

机器学习（17）---支持向量机(SVM)

支持向量机 一、概述1.1 介绍1.2 工作原理1.3 三层理解 二、sklearn.svm.SVC2.1 查看数据集2.2 contour函数2.3 画决策边界&#xff1a;制作网格2.4 建模画图 三、非线性情况推广3.1 查看数据集3.2 线性画图3.3 为非线性数据增加维度并绘制3D图像 四、核函数 一、概述 1.1 介绍…
阅读更多...
记一次 mysql 数据库定时备份

记一次 mysql 数据库定时备份

环境&#xff1a;Centos 7.9 数据库&#xff1a;mysql 8.0.30 需求&#xff1a;生产环境 mysql 数据&#xff08;约670MB&#xff09;备份。其中存在大字段、longblob字段 参考博客&#xff1a;Linux环境下使用crontab实现mysql定时备份 - 知乎 一、数据库备份 1. 备份脚本。创…
阅读更多...
Python项目Flask ipv6双栈支持改造

Python项目Flask ipv6双栈支持改造

一、背景 Flask 是一个微型的（轻量）使用Python 语言开发的 WSGI Web 框架（一组库和模块），基于Werkzeug WSGI工具箱/库和Jinja2 模板引擎，当然，Python的WEB框架还有：Django、Tornado、Webpy，这暂且不提。 Flask使用BSD授权。 Flask也被称为microframework（微框架），F…
阅读更多...
RFID技术在工业智能制造生产线中的应用

RFID技术在工业智能制造生产线中的应用

随着自动化和信息化的快速发展&#xff0c;工业智能制造成为制造业的重要趋势&#xff0c;在制造商的生产线上&#xff0c;准确获取和管理工艺流程等各个环节的信息至关重要&#xff0c;作为物联网感知层的核心组成部分&#xff0c;RFID技术以其非接触式、无感知的特点&#xf…
阅读更多...
隔山打牛：金融大崩溃

隔山打牛：金融大崩溃

当2004-2006年美联储主席格林斯潘在任期的末尾一鼓作气把联邦利率从1%拉高到5%&#xff0c;然后把美联储主席的位子交给继任者伯南克的时候&#xff0c;没有人意识到接下来将要发生何等巨变。 图&#xff1a;美国联邦利率 伯南克把利率稳定在5.3%附近的高位一年左右时间&#x…
阅读更多...
【ArcGIS】基本概念-矢量空间分析

【ArcGIS】基本概念-矢量空间分析

栅格数据与矢量数据 1.1 栅格数据 栅格图是一个规则的阵列&#xff0c;包含着一定数量的像元或者栅格 常用的栅格图格式有&#xff1a;tif&#xff0c;png&#xff0c;jpeg/jpg等 1.2 矢量数据 矢量图是由一组描述点、线、面&#xff0c;以及它们的色彩、位置的数据&#x…
阅读更多...
无涯教程-JavaScript - AVEDEV函数

无涯教程-JavaScript - AVEDEV函数

描述 AVEDEV函数返回数据点与其平均值的绝对偏差的平均值。 AVEDEV是数据集中变异性的量度。 语法 AVEDEV (number1, [number2] ...)争论 Argument描述Required/OptionalNumber11 to 255 arguments for which you want the average of the absolute deviations.Requirednum…
阅读更多...
趴趴雅思作文修改

趴趴雅思作文修改

前言 在网上试了下趴趴雅思作文修改的服务&#xff0c;淘宝上直接就可以购买&#xff0c;首次有优惠&#xff0c;之后还是挺贵的。 用了下感觉&#xff0c;有用还是有用的&#xff0c;但是挺贵的&#xff0c;一次40&#xff0c;不值。他给我作文的评分是7分&#xff0c;应该给…
阅读更多...
fineReport11.0.4版本新建数据链接

fineReport11.0.4版本新建数据链接

需要以下几步&#xff1a; 1.设计器和服务器都需要安装对应数据库的驱动&#xff08;已安装就跳过&#xff09; 对应驱动可以在官网下载&#xff0c;百度搜下有教程 2.服务器没有驱动需要上传驱动 2.1 服务器上传驱动文件&#xff0c;需要修改finedb中的fine_conf_entity表…
阅读更多...
Mobpush上线跨时区推送功能，助力中国开发者应用出海

Mobpush上线跨时区推送功能，助力中国开发者应用出海

近年来随着国内移动应用存量市场饱和&#xff0c;国内移动应用厂商转向”移动出海“&#xff0c;把握国际市场中存在结构性发展机会&#xff0c;提升中国品牌移动应用的知名度和影响力。根据公开资料显示&#xff0c;中国应用开发者中有79.1%计划出海&#xff0c;其中43%的开发…
阅读更多...
极光笔记 | 大语言模型插件

极光笔记 | 大语言模型插件

在人工智能领域&#xff0c;大语言模型&#xff08;LLMs&#xff09;是根据预训练数据集进行”学习“&#xff0c;获取可以拟合结果的参数&#xff0c;虽然随着参数的增加&#xff0c;模型的功能也会随之增强。但无论专业领域的小模型&#xff0c;还是当下最火、效果最好的大模…
阅读更多...
分享一下微信公众号怎么实现积分商城功能

分享一下微信公众号怎么实现积分商城功能

微信公众号作为一种社交媒体平台&#xff0c;可以帮助商家与消费者进行互动和沟通。除了实现微信拼团活动外&#xff0c;微信公众号还可以实现积分商城功能&#xff0c;提高消费者的参与度和忠诚度。本文将介绍如何在微信公众号实现积分商城功能。 一、了解积分商城 积分商城是…
阅读更多...
邮件如何避免进垃圾箱

邮件如何避免进垃圾箱

邮件营销是一种常见的营销手段&#xff0c;可以帮助企业向大量目标群体发送营销信息&#xff0c;因此邮件营销被广泛应用于促销活动、产品推广、新闻发布、客户维护等场景。然而随着垃圾邮件的泛滥&#xff0c;国内外大部分的电子邮件服务商都采取了越来越严厉的垃圾邮件过滤机…
阅读更多...
系统集成|第九章(笔记)

系统集成|第九章(笔记)

目录 第九章 成本管理9.1 成本管理概念及相关术语9.2 主要过程9.2.1 制订成本管理计划9.2.2 成本估算9.2.3 成本预算9.2.4 成本控制 上篇&#xff1a;第八章、进度管理 第九章 成本管理 9.1 成本管理概念及相关术语 概述&#xff1a;项目成本管理就是要确保在批准的预算内完成…
阅读更多...
怎么优化企业内部的报修流程？有什么好用的企业智能报修管理系统？

怎么优化企业内部的报修流程？有什么好用的企业智能报修管理系统？

随着数字化转型成为企业的新风向&#xff0c;传统的企业报修方式已经变得不够便捷。传统的报修流程往往依赖于企业内部的组织架构&#xff0c;给员工和用户带来了许多麻烦。报修人需要注册、登录、下载和安装相关软件&#xff0c;而且一个故障报修还需要进行多个步骤的操作才能…
阅读更多...
AI生成原创文章的工具-AI生成原创文字软件

AI生成原创文章的工具-AI生成原创文字软件

让我们来了解一下AI生成原创文章的概念。这是指使用人工智能技术&#xff0c;特别是自然语言处理模型&#xff0c;来生成文字内容&#xff0c;这些文字看起来就像是由我们创作的。这种技术已经在自媒体、新闻媒体、博客和其他各种网站上广泛使用。但是&#xff0c;问题出现在于…
阅读更多...
上位机在自动化控制中的作用和优势是什么？

上位机在自动化控制中的作用和优势是什么？

上位机在自动化控制中的作用和优势是什么&#xff1f; 自动化控制编程领域包括单片机、PLC、机器视觉和运动控制等方向。输入“777”&#xff0c;即刻获取关于上位机开发和数据可视化的专业学习资料&#xff0c;近年来&#xff0c;上位机编程逐渐兴起&#xff0c;正在逐步替代…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023