相关博客
【自然语言处理】【大模型】RWKV:基于RNN的LLM
【自然语言处理】【大模型】CodeGen:一个用于多轮程序合成的代码大语言模型
【自然语言处理】【大模型】CodeGeeX:用于代码生成的多语言预训练模型
【自然语言处理】【大模型】LaMDA:用于对话应用程序的语言模型
【自然语言处理】【大模型】DeepMind的大模型Gopher
【自然语言处理】【大模型】Chinchilla:训练计算利用率最优的大语言模型
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型
【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍
【自然语言处理】【大模型】BLOOM:一个176B参数且可开放获取的多语言模型
【自然语言处理】【大模型】PaLM:基于Pathways的大语言模型
【自然语言处理】【chatGPT系列】大语言模型可以自我改进
【自然语言处理】【ChatGPT系列】FLAN:微调语言模型是Zero-Shot学习器
【自然语言处理】【ChatGPT系列】ChatGPT的智能来自哪里?
基于Transformer的LLM已经取得了巨大的成功,但是其在显存消耗和计算复杂度上都很高。RWKV是一个基于RNN的LLM,其能够像Transformer那样高效的并行训练,也能够像RNN那样高效的推理。
一、背景知识
1. RNN
RNN是指一类神经网络模型结构,其中最具有代表性的是LSTM:
f
t
=
σ
g
(
W
f
x
t
+
U
f
h
t
−
1
+
b
f
)
i
t
=
σ
g
(
W
i
x
t
+
U
i
h
t
−
1
+
b
i
)
o
t
=
σ
g
(
W
o
x
t
+
U
o
h
t
−
1
+
b
o
)
c
~
t
=
σ
c
(
W
c
x
t
+
U
c
h
t
−
1
+
b
c
)
c
t
=
f
t
⊙
c
t
−
1
+
i
t
⊙
c
~
t
h
t
=
o
t
⊙
σ
h
(
c
t
)
\begin{align} f_t&=\sigma_g(W_fx_t+U_f h_{t-1}+b_f) \tag*{(1)} \\ i_t&=\sigma_g(W_ix_t+U_i h_{t-1}+b_i) \tag*{(2)} \\ o_t&=\sigma_g(W_ox_t+U_o h_{t-1}+b_o) \tag*{(3)} \\ \tilde{c}_t&=\sigma_c(W_cx_t+U_c h_{t-1}+b_c) \tag*{(4)} \\ c_t&=f_t\odot c_{t-1}+i_t\odot\tilde{c}_t \tag*{(5)} \\ h_t&=o_t\odot\sigma_h(c_t) \tag*{(6)} \end{align} \\
ftitotc~tctht=σg(Wfxt+Ufht−1+bf)=σg(Wixt+Uiht−1+bi)=σg(Woxt+Uoht−1+bo)=σc(Wcxt+Ucht−1+bc)=ft⊙ct−1+it⊙c~t=ot⊙σh(ct)(1)(2)(3)(4)(5)(6)
其中,
x
t
x_t
xt是当前时间步的输入,
h
t
−
1
h_{t-1}
ht−1是上一个时间步的隐藏状态,所有的
W
W
W、
U
U
U和
b
b
b都是可学习参数,
σ
\sigma
σ表示
sigmoid
\text{sigmoid}
sigmoid函数。
f
t
f_t
ft是“遗忘门”,用来控制前一个时间步上传递信息的比例;
i
t
i_t
it是“输入门”,用于控制当前时间步保留的信息比例;
o
t
o_t
ot是"输出门",用于产生最终的输出。
2. Transformers和AFT
Transformer是NLP中主流的一种模型架构,其依赖于注意力机制来捕获所有输入和输出tokens的关系:
Attn
(
Q
,
K
,
V
)
=
softmax
(
Q
K
⊤
)
V
(7)
\text{Attn}(Q,K,V)=\text{softmax}(QK^\top)V \tag{7} \\
Attn(Q,K,V)=softmax(QK⊤)V(7)
为了简洁,这里忽略了多头和缩放因子
1
d
k
\frac{1}{\sqrt{d_k}}
dk1。
Q
K
⊤
QK^\top
QK⊤是序列中每个token之间的成对注意力分数,其能够被分解为向量表示:
Attn
(
Q
,
K
,
V
)
t
=
∑
i
=
1
T
e
q
t
⊤
k
i
∑
i
=
1
T
e
q
t
⊤
k
i
v
i
=
∑
i
=
1
T
e
q
t
⊤
k
i
v
i
∑
i
=
1
T
e
q
t
⊤
k
i
(8)
\text{Attn}(Q,K,V)_t=\sum_{i=1}^T\frac{e^{q_t^\top k_i}}{\sum_{i=1}^T e^{q_t^\top k_i}}v_i=\frac{\sum_{i=1}^T e^{q_t^\top k_i}v_i}{\sum_{i=1}^T e^{q_t^\top k_i}}\tag{8} \\
Attn(Q,K,V)t=i=1∑T∑i=1Teqt⊤kieqt⊤kivi=∑i=1Teqt⊤ki∑i=1Teqt⊤kivi(8)
在AFT中,设计了一种注意力变体:
Attn
+
(
W
,
K
,
V
)
t
=
∑
i
=
1
t
e
w
t
,
i
+
k
i
v
i
∑
i
=
1
t
e
w
t
,
i
+
k
i
(9)
\text{Attn}^+(W,K,V)_t=\frac{\sum_{i=1}^t e^{w_{t,i}+k_i}v_i}{\sum_{i=1}^t e^{w_{t,i}+k_i}} \tag{9} \\
Attn+(W,K,V)t=∑i=1tewt,i+ki∑i=1tewt,i+kivi(9)
其中,
{
w
t
,
i
}
∈
R
T
×
T
\{w_{t,i}\}\in R^{T\times T}
{wt,i}∈RT×T是可学习的位置偏差,每个
w
t
,
i
w_{t,i}
wt,i是一个标量。
受AFT启发,在RWKV中的
w
t
,
i
w_{t,i}
wt,i是一个乘以相对位置的时间衰减向量:
w
t
,
i
=
−
(
t
−
i
)
w
(10)
w_{t,i}=-(t-i)w \tag{10} \\
wt,i=−(t−i)w(10)
其中,
w
∈
(
R
≥
0
)
d
w\in (R_{\geq 0})^d
w∈(R≥0)d,
d
d
d是通道数。这里需要
w
w
w是非负来保证
e
w
t
,
i
≤
1
e^{w_{t,i}}\leq 1
ewt,i≤1并且每个信道随时间衰减。
二、RWKV(Receptance Weighted Key Value)
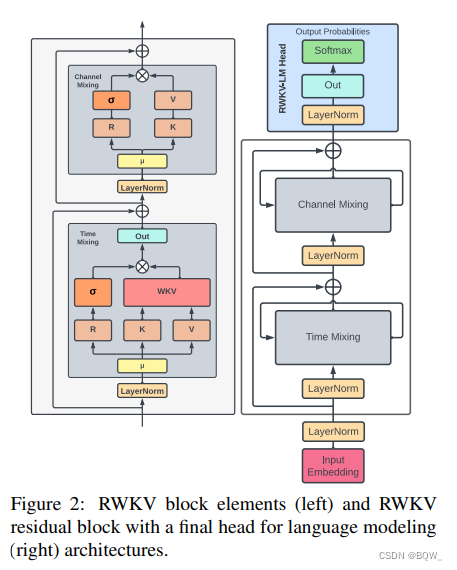
RWKV由一系列的基本Block组成,每个Block则由time-mixing block和channel-mixing block组成的(如上图所示)。
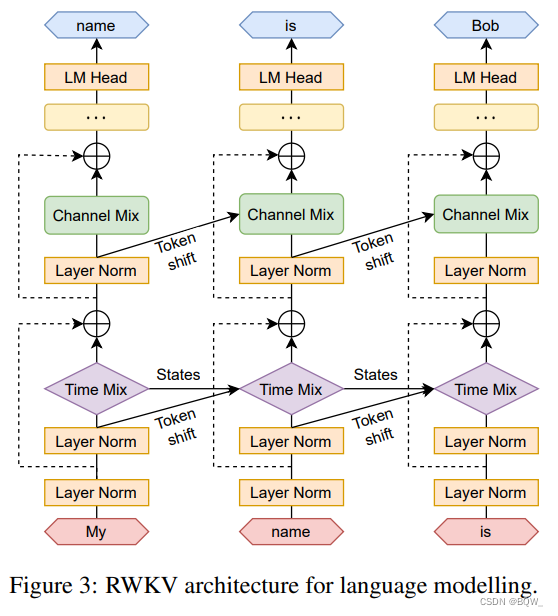
RWKV递归的形式可以看做是当前输入和前一个时间不输入的线性插值,如上图所示。
1. Time-mixing block
Time-mixing block的作用同Self-Attention相同,就是提供全局token的交互。细节如下:
r
t
=
W
r
⋅
(
μ
r
x
t
+
(
1
−
u
r
)
x
t
−
1
)
k
t
=
W
k
⋅
(
μ
k
x
t
+
(
1
−
u
k
)
x
t
−
1
)
v
t
=
W
v
⋅
(
μ
v
x
t
+
(
1
−
μ
v
)
x
t
−
1
)
w
k
v
t
=
∑
i
=
1
t
−
1
e
−
(
t
−
1
−
i
)
w
+
k
i
v
i
+
e
u
+
k
t
v
t
∑
i
=
1
t
−
1
e
−
(
t
−
1
−
i
)
w
+
k
i
+
e
u
+
k
t
o
t
=
W
o
⋅
(
σ
(
r
t
)
⊙
w
k
v
t
)
\begin{align} r_t&=W_r\cdot(\mu_rx_t+(1-u_r)x_{t-1}) \tag*{(11)} \\ k_t&=W_k\cdot(\mu_kx_t+(1-u_k)x_{t-1}) \tag*{(12)} \\ v_t&=W_v\cdot(\mu_vx_t+(1-\mu_v)x_{t-1}) \tag*{(13)} \\ wkv_t&=\frac{\sum_{i=1}^{t-1}e^{-(t-1-i)w+k_i}v_i+e^{u+k_t}v_t}{\sum_{i=1}^{t-1}e^{-(t-1-i)w+k_i}+e^{u+k_t}} \tag*{(14)} \\ o_t&=W_o\cdot(\sigma(r_t)\odot wkv_t) \tag*{(15)} \end{align} \\
rtktvtwkvtot=Wr⋅(μrxt+(1−ur)xt−1)=Wk⋅(μkxt+(1−uk)xt−1)=Wv⋅(μvxt+(1−μv)xt−1)=∑i=1t−1e−(t−1−i)w+ki+eu+kt∑i=1t−1e−(t−1−i)w+kivi+eu+ktvt=Wo⋅(σ(rt)⊙wkvt)(11)(12)(13)(14)(15)
所有的
μ
\mu
μ和
W
W
W都是可训练参数,
r
t
r_t
rt、
k
t
k_t
kt和
v
t
v_t
vt是当前输入
x
t
x_t
xt和上一个时间步输入
x
t
−
1
x_{t-1}
xt−1的加权投影。
公式(14)中, w w w和 u u u是可训练参数,分子的第一项 ∑ i = 1 t − 1 e − ( t − 1 − i ) w + k i v i \sum_{i=1}^{t-1}e^{-(t-1-i)w+k_i}v_i ∑i=1t−1e−(t−1−i)w+kivi表示前 t − 1 t-1 t−1步的加权结果, − ( t − 1 − i ) w + k i -(t-1-i)w+k_i −(t−1−i)w+ki是随相对距离逐步衰减; e u + k t v t e^{u+k_t}v_t eu+ktvt则是当前时间步的结果。
公式(15)中,则通过 σ ( r t ) \sigma(r_t) σ(rt)控制最终输出的比例。
2. Channel-mixing block
Channel-mixing block类似于Transformer中的FFN部分,细节如下:
r
t
=
W
r
⋅
(
μ
r
x
t
−
(
1
−
μ
r
)
x
t
−
1
)
k
t
=
W
k
⋅
(
μ
k
x
t
−
(
1
−
μ
k
)
x
t
−
1
)
o
t
=
σ
(
r
t
)
⊙
(
W
v
⋅
max
(
k
t
,
0
)
2
)
\begin{align} r_t&=W_r\cdot(\mu_rx_t-(1-\mu_r)x_{t-1}) \tag*{(16)} \\ k_t&=W_k\cdot(\mu_kx_t-(1-\mu_k)x_{t-1}) \tag*{(17)} \\ o_t&=\sigma(r_t)\odot(W_v\cdot\max(k_t,0)^2) \tag*{(18)} \\ \end{align} \\
rtktot=Wr⋅(μrxt−(1−μr)xt−1)=Wk⋅(μkxt−(1−μk)xt−1)=σ(rt)⊙(Wv⋅max(kt,0)2)(16)(17)(18)
三、并行训练和序列解码
RWKV可以类似Transformer那样高效的并行。设batch size为B、seq_length为T、channels为d,计算量主要来自于矩阵乘法 W □ , □ ∈ { r , k , v , o } W_\square,\square\in \{r,k,v,o\} W□,□∈{r,k,v,o},单层的时间复杂度为 O ( B T d 2 ) O(BTd^2) O(BTd2)。此外,更新注意力分数 w k v t wkv_t wkvt需要顺序扫描,其时间复杂度为 O ( B T d ) O(BTd) O(BTd)。矩阵乘法可以像Transformer那样并行,但是WKV的计算是依赖时间步的,所以只能在其他维度上并行。
RWKV具有类似RNN的结构,解码时将 t t t步的输出作为 t + 1 t+1 t+1步的输入。相比于自注意力机制随着序列长度,计算复杂度呈平方次增长,RWKV则是与序列长度呈线性关系。因此,RWKV能够更高效的处理更长的序列。