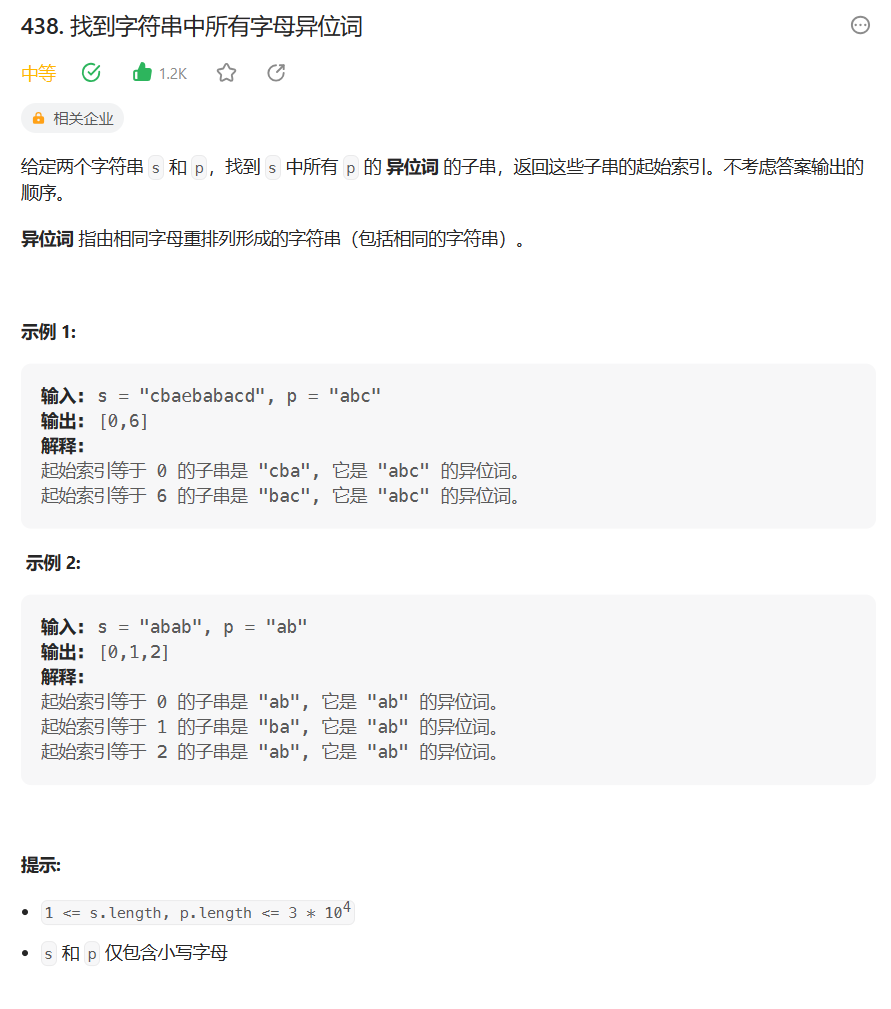
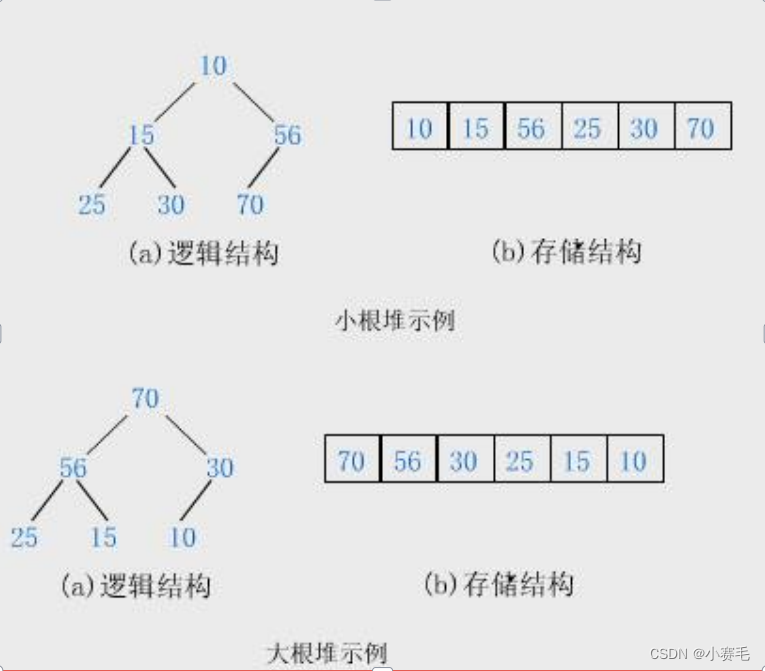
堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。
大堆：任何父亲≥孩子
小堆：任何父亲≤孩子
接下来，我们要做的便是对堆进行增加和删除：
首先是增加操作，我们这里采用向上调整的方式来进行增加：
void AdjustUP(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}时间复杂度：O(logN)
比如我们有这样一组数据：
int a[] = { 65,100,70,32,50,60 };然后对其进行操作如下;
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//扩容
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUP(php->a, php->size - 1);
}运行结果为：
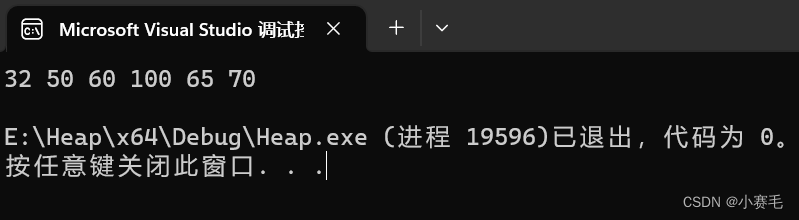
结果：
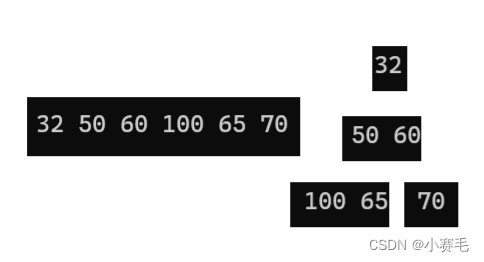
嘿嘿，怎么着？这不就是小堆嘛？
那么呢，接下来我们便进行数据的删除操作：
我们先来考虑这样一个问题：删除哪个数据最有价值呢？
显然是删除根because挪动覆盖第一个位置根，关系全乱了，剩下的值，不一定是堆
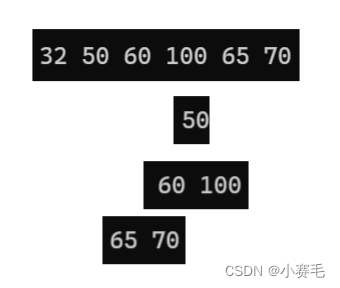你看，你看，这不是没乱吗？
雷布斯：这绝对是来捣乱的（这种情况呢，显然只是一个巧合）
不信，我们再来看一个：
你看全乱了，所以这种方式好不好呢？
那不好怎么办呢？别慌，让我们娓娓道来：
我们不影响其他位置，加上尾插和尾删的效率很好，所以只把要删除的元素和最后一个元素换换位置，你看：
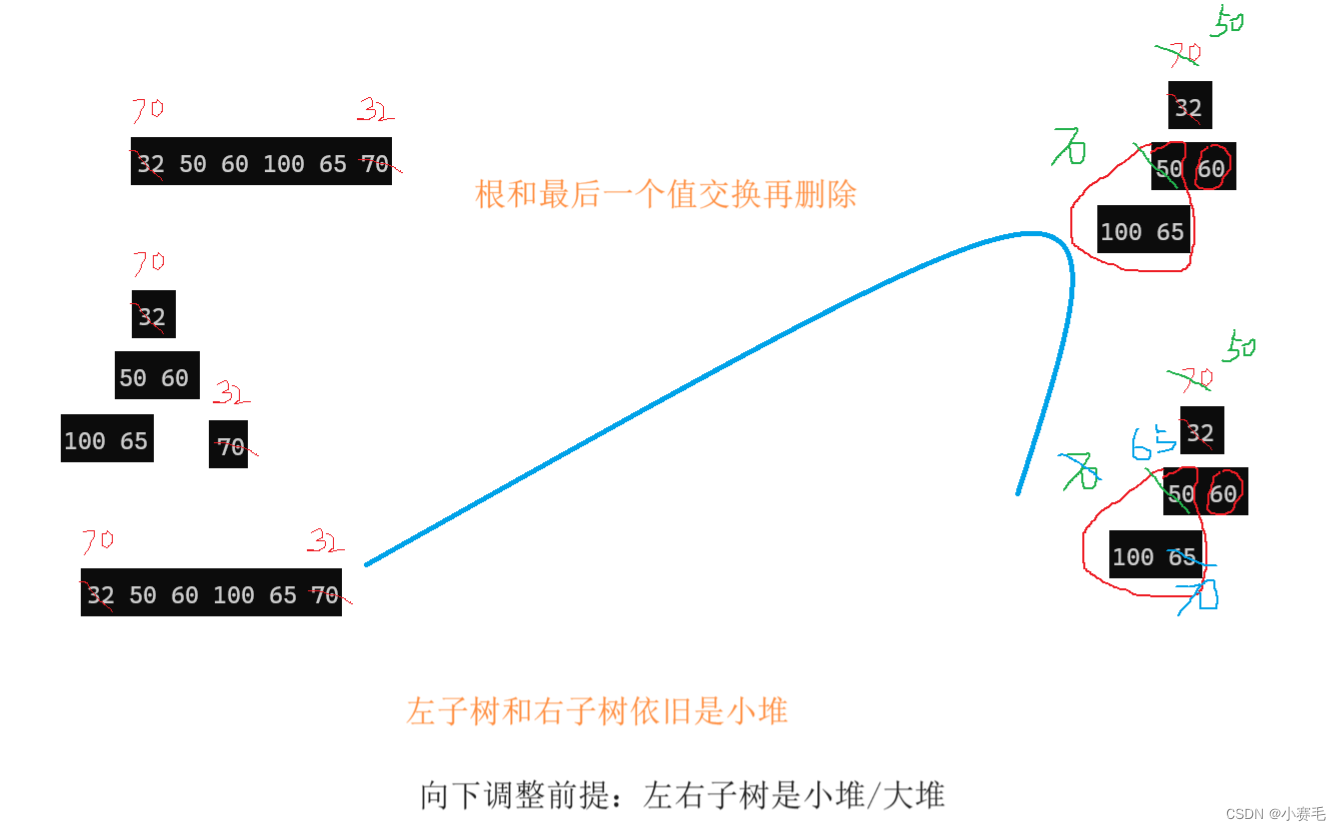
向下调整：
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
//找出小的那个孩子
if (child+1 < n && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
//继续向下调整
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}时间复杂度：O(logN)
其次，我们仔细看，经过这一系列操作，我们是不是还把这一组数据中的次小元素给找了出来？
那我们再继续pop，是不是又找到了第三小？依次反复……是不是就成为了排序
我们来操作一下，对某个数组进行排序。
如果要求的是升序，应该选择 大堆 还是 小堆 呢？
升序：建大堆
堆顶跟最后一个交换 最大的数据排好了 剩下数据向下调整，选出次大的，代价是logN
合计是：N*logN
//升序
void HeapSort(int* a, int n)
{
//建堆 （大堆）or （小堆）
for (int i = 1; i < n; i++)
{
AdjustUP(a, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
