解析：

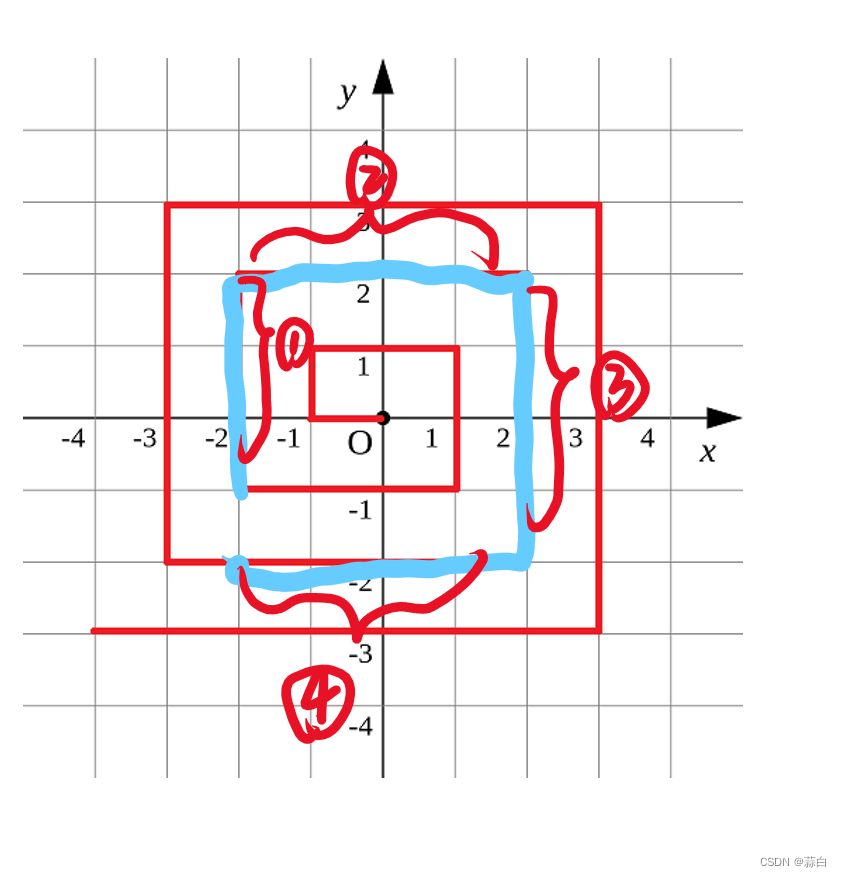
        把每个区间段分成左闭右开区间，我们可以观察到，每个区间的饼干数量为 ( r - l ) / d 上取整。

        所以先计算不删除某个点的饼干总和init，然后遍历所有点，将这个点删除。所以删除某个点后剩余数量为：

        

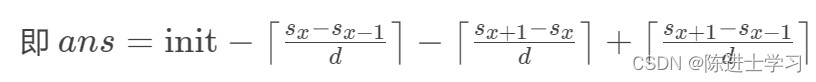
        找出最小值并且统计数量。

        需要注意的是，因为如果没有 1 号位，那么 1 号位同样要吃一个饼干，所以设置一个 1 号虚拟位放在 a[ 0 ]，这样就算有1号，那么 a[1]和a[0]的距离也是0，不影响结果。  

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int t,n,m,d,x,a[N];
int func(int x,int y){
	if((y-x)%d==0) return (y-x)/d;
	return (y-x)/d+1;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d%d",&n,&m,&d);
		int f=0;
		for(int i=1;i<=m;i++){
			scanf("%d",&a[i]);
			if(x==1) f=1;
		}
		a[0]=1;
		a[m+1]=n+1;
		int cnt=0;
		for(int i=0;i<=m;i++){
			cnt+=func(a[i],a[i+1]);
		}
		int ans,res=-1;
		for(int i=1;i<=m;i++){
			int p=cnt-func(a[i-1],a[i])-func(a[i],a[i+1])+func(a[i-1],a[i+1]);
			if(res==-1||p<res){
				ans=1;
				res=p;
			}
			else if(p==res) ans++;
		}
		printf("%d %d\n",res,ans);
	}
	return 0;
}