文章目录
- 1、高中几个知识点
- exp(n)
- log(n)
- lgx、lnx
- 电容充放电公式
- 2、双积分型ADC工作原理
- 3、SAR和∑-Δ型模数转换器(ADC)
1、高中几个知识点
exp(n)
exp函数即指数函数:e的n次方的函数,自然常数e=2.718281828459045
举例:
exp(0) =
e
0
e^{0}
e0=1;
exp(1) =
e
1
e^{1}
e1 = 2.718281828459045
exp(2) =
e
2
e^{2}
e2 = 7.38905609893065
…
exp(n) =
e
n
e^{n}
en
log(n)
#
l
o
g
10
log_{10}
log10:以10为底数的对数,对数是对求幂的逆运算
#
l
o
g
2
log_2
log2:以2为底数的对数,对数是对求幂的逆运算
举例:
l
o
g
2
(
4
)
log_2(4)
log2(4) =2;以2为底,求2的多少次方为4,即2的2次方为4
l
o
g
2
(
8
)
log_2(8)
log2(8) =3;以2为底,求2的多少次方为8,即2的2次方为8
l
o
g
2
(
n
)
log_2(n)
log2(n);以2为底,求2的多少次方为n
#log默认以e为底
l
o
g
(
n
)
log(n)
log(n) 等价与
l
o
g
e
(
n
)
log_e(n)
loge(n)
举例:
l
o
g
(
e
)
log(e)
log(e) =
l
o
g
e
(
e
)
log_e(e)
loge(e) = 1
l
o
g
(
e
2
)
log(e^2)
log(e2) =
l
o
g
e
(
e
2
)
log_e(e^2)
loge(e2) = 2
…
l
o
g
(
e
n
)
log(e^n)
log(en) =
l
o
g
e
(
e
n
)
log_e(e^n)
loge(en) = n
lgx、lnx
l
g
x
lg x
lgx 等价与
l
o
g
10
(
x
)
log_{10}(x)
log10(x)
l
n
x
ln x
lnx 等价与
e
x
e^x
ex
举例:
l
g
1
lg1
lg1 = 0
l
g
10
lg{10}
lg10 = 1
l
g
1
0
2
lg{10^2}
lg102 = 2
…
l
g
1
0
n
lg{10^n}
lg10n = n
l
n
0
ln 0
ln0 =
e
0
e^0
e0 = 1
l
n
1
ln 1
ln1 =
e
1
e^1
e1
l
n
2
ln 2
ln2 =
e
2
e^2
e2
…
l
n
n
ln n
lnn =
e
n
e^n
en
电容充放电公式
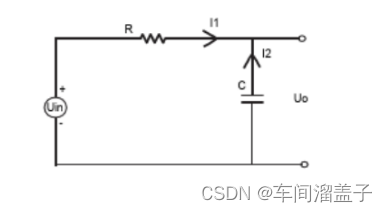
设,V0 为电容上的初始电压值;V1 为电容最终可充到或放到的电压值;Vt 为t时刻电容上的电压值。则:
Vt=V0 +(V1-V0)× [1-exp(-t/RC)]
即:
Vt=V0 +(V1-V0)× [1-
e
(
−
t
/
R
C
)
e^{(-t/RC)}
e(−t/RC)]
时间t:
t = RC × Ln[(V1 - V0)/(V1 - Vt)]
即:
t = RC ×
e
[
(
V
1
−
V
0
)
/
(
V
1
−
V
t
)
]
e^{[(V1 - V0)/(V1 - Vt)]}
e[(V1−V0)/(V1−Vt)]
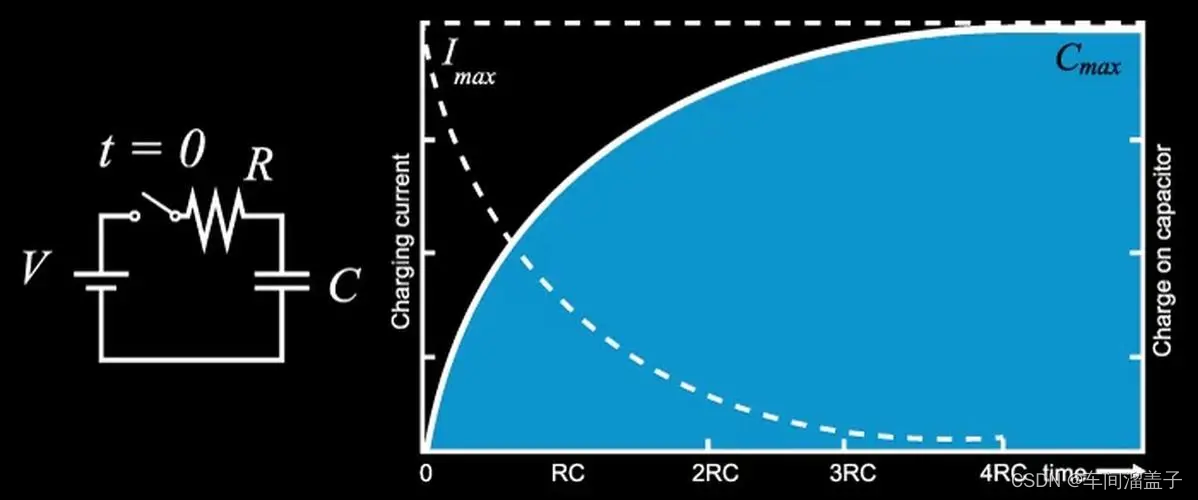
电容充放电曲线如下:
2、双积分型ADC工作原理
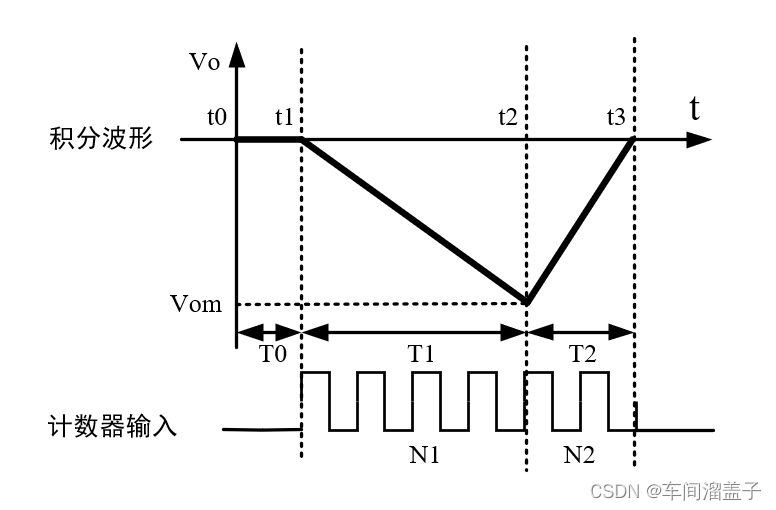
先将模拟电压转换成与其大小成正比的时间间隔,再利用基准时钟源并通过计数器将时间间隔转换成数字量输出。
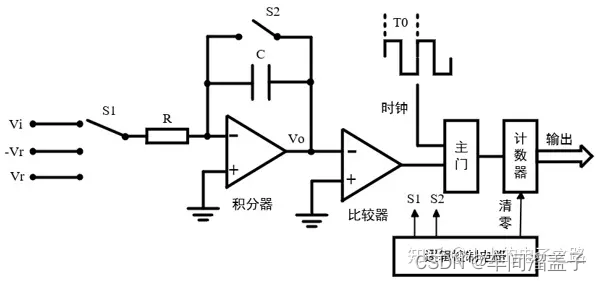
双积分型ADC是通过对两次积分过程(对被测电压的定时积分和对参考电压的定值积分)的比较,从而得到被测电压值。上图是双积分型ADC的电路原理框图,主要包括积分器、过零比较器、计数器以及逻辑控制电路。
双积分型ADC的工作过程分为三个阶段,分别是复零阶段、定时积分阶段、定值积分阶段。
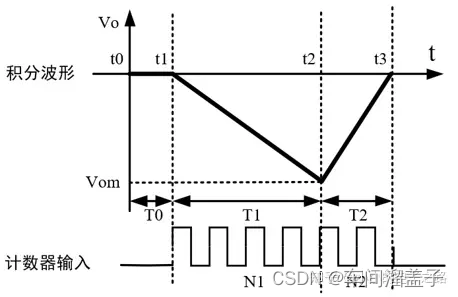
1、复零阶段(t0-t1):在此阶段开关S2闭合T0时间,电容C短路,积分器的输出回归到零;
2、定时积分阶段(t1-t2):在此阶段接入被测电压,此时积分器的输出Vo从零开始线性增长,经过规定的T1时间后增长到最大值Vom,此时有
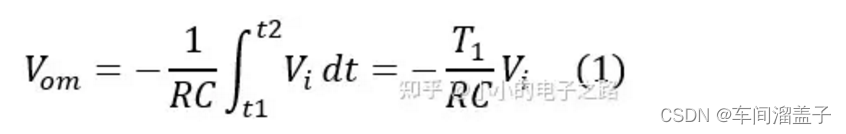
3、定值积分阶段(t2-t3):在此阶段接入与被测电压符号相反的参考电压,使积分器的输出Vo从Vom开始线性减小至零,此时有
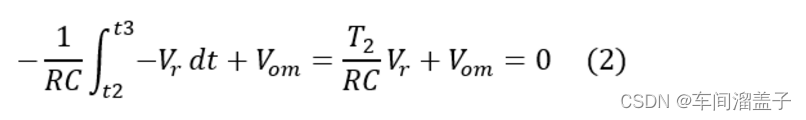
整理公式(1)、(2)可得

由于T1、T2是对周期为T0的时钟信号计数得到的,计数值分别为N1、N2,因此有
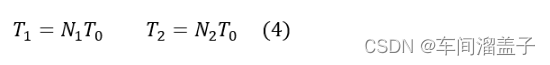
整理公式(3)、(4)可得

由于N1、Vr为定值,因此
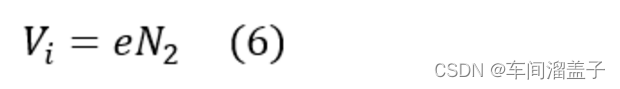
其中e称为双积分型ADC的刻度系数。
通过公式(6)发现,可以通过计数结果N2表示被测电压Vi,因此,N2即为双积分型ADC的转换结果。
从这个公式可以看出,双斜坡积分ADC的好处之一很明显:测量结果与电路元件的值(其中的R和C)无关。然而,这并不意味着,R和C在双斜坡积分ADC中不重要(下面将解释这一问题)。
注意到在下图中,在上升阶段电压是向上升高的,在下降阶段电压是向下降低的。在实际应用中,由于比较器使用的是运放的负反馈,施加一个正向电压Vin实际会使输出下降,所以这里的“上”和“下”可以理解为积分电容充电的过程。

双斜坡积分型ADC的分辨率主要由下降阶段的时间长度和时间测量分辨率(例如控制器时钟的频率)来决定的(译者:也就是速度和分辨率这一对矛盾的原因)。期望的分辨率(用bits数表示) 是满量程输入时,下降时间的最小长度。(Vin = -Vref)
在满程输入的测量过程中,积分器输出的斜坡在上升和下降阶段是相同的(方向相反)。也就是上升和下降阶段的时间相等(),总的测量时间则为。 因此,满程输入的总的测量时间是基于期望的分辨率和控制器的时钟频率的。如下式:
举个栗子:如果期望得到16bits的分辨率,控制器时钟频率是10MHz,那么测量时间计算下来就是13.1ms(也即是每秒钟76个采样)。采样时间可以靠牺牲分辨率得到改善。如果分辨率降低到10bits,那么在同样的10MHz的时钟频率下,测量时间就降低到仅为0.2ms(每秒钟4900个采样)。
我个人理解是:电容决定了单位时间内数据的转换频率,如果选择大电容,采样率变低,数据更为精准;如果选择小电容,采样率变高,数据精度更差。也就是说信号过小,电容应该选择更大,降低采样率提高精度;信号比较大,无需太大的电容,数据也能比较精确。所以选择电容大小直接影响采样结果的精度;
3、SAR和∑-Δ型模数转换器(ADC)
逐次逼近式(SAR)A/D转换器(SAR)的基本原理是:将待转换的模拟输入信号与一个推测信号进行比较,根据二者大小决定增大还是减小输入信号,以便向模拟输入信号逼进。推测信号由D/A转换器的输出获得,当二者相等时,向D/A转换器输入的数字信号就对应的时模拟输入量的数字量。这种A/D转换器一般速度很快,但精度一般不高。常用的有ADC0801、ADC0802、AD570等。
∑-Δ型模也就是Sigma-Delta
双积分式A/D转换器的基本原理是:先对输入模拟电压进行固定时间的积分,然后转为对标准电压的反相积分,直至积分输入返回初始值,这两个积分时间的长短正比于二者的大小,进而可以得出对应模拟电压的数字量。这种A/D转换器的转换速度较慢,但精度较高。由双积分式发展为四重积分、五重积分等多种方式,在保证转换精度的前提下提高了转换速度







![[php] 文件上传的一个项目emmm](https://img-blog.csdnimg.cn/1374261b20484721b9d07abd12cb0e6f.png#pic_center)