文章目录
- 矩阵分解
- LU分解
- QR分解
- 特征值分解
- 奇异值分解
- 奇异值分解
- 矩阵的基本子空间
- 奇异值分解的性质
- 矩阵的外积展开式
矩阵分解
矩阵的因式分解是把矩阵表示为多个矩阵的乘积,这种结构更便于理解和计算。
LU分解
设
A
A
A 是
m
×
n
m\times n
m×n 矩阵,若
A
A
A 可以写成乘积
A
=
L
U
A=LU
A=LU
其中,
L
L
L 为
m
m
m 阶下三角方阵,主对角线元素全是1。
U
U
U 为
A
A
A 得到一个行阶梯形矩阵。这样一个分解称为LU分解。
L
L
L 称为单位下三角方阵。
我们先来看看,LU分解的一个应用。当
A
=
L
U
A=LU
A=LU 时,方程
A
x
=
b
A\mathbf x=\mathbf b
Ax=b 可写成
L
(
U
x
)
=
b
L(U\mathbf x)=\mathbf b
L(Ux)=b,于是分解为下面两个方程
L
y
=
b
U
x
=
y
L\mathbf y=\mathbf b \\ U\mathbf x=\mathbf y
Ly=bUx=y
因为
L
L
L 和
U
U
U 都是三角矩阵,每个方程都比较容易解。
LU 分解算法:本节只讲述仅用行倍加变换求解。可以证明,单位下三角矩阵的乘积和逆也是单位下三角矩阵 。此时,可以用行倍加变换寻找
L
L
L 和
U
U
U 。假设存在单位下三角初等矩阵
P
1
,
⋯
,
P
s
P_1,\cdots,P_s
P1,⋯,Ps 使
P
1
⋯
P
s
A
=
U
P_1\cdots P_sA=U
P1⋯PsA=U
于是便得到了
U
U
U 和
L
L
L
L
=
(
P
1
,
⋯
,
P
s
)
−
1
L=(P_1,\cdots,P_s)^{-1}
L=(P1,⋯,Ps)−1
QR分解
如果 m × n m\times n m×n 矩阵 A A A 的列向量线性无关,那么 A A A 可以分解为 A = Q R A=QR A=QR,其中 Q Q Q 是一个 m × n m\times n m×n 正交矩阵,其列为 col A \text{col }A col A 的一组标准正交基, R R R 是一个上 n × n n\times n n×n 三角可逆矩阵,且其对角线上的元素全为正数。
证:矩阵
A
=
(
x
1
,
x
2
,
⋯
,
x
n
)
A=(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n)
A=(x1,x2,⋯,xn) 的列向量是
col
A
\text{col }A
col A 的一组基,使用施密特正交化方法可以构造一组标准正交基
u
1
,
u
2
,
⋯
,
u
n
\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n
u1,u2,⋯,un ,取
Q
=
(
u
1
,
u
2
,
⋯
,
u
n
)
Q=(\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n)
Q=(u1,u2,⋯,un)
因为在正交化过程中
x
k
∈
span
{
x
1
,
⋯
,
x
k
}
=
span
{
u
1
,
⋯
,
u
k
}
,
k
=
1
,
2
,
⋯
,
n
\mathbf x_k\in\text{span}\{\mathbf x_1,\cdots,\mathbf x_k\}=\text{span}\{\mathbf u_1,\cdots,\mathbf u_k\},\quad k=1,2,\cdots,n
xk∈span{x1,⋯,xk}=span{u1,⋯,uk},k=1,2,⋯,n 。所以
x
k
\mathbf x_k
xk 可线性表示为
x
k
=
r
1
k
u
1
+
⋯
+
r
k
k
u
k
+
0
⋅
u
k
+
1
+
⋯
+
0
⋅
u
n
\mathbf x_k=r_{1k}\mathbf u_1+\cdots+r_{kk}\mathbf u_k+0\cdot\mathbf u_{k+1}+\cdots+0\cdot\mathbf u_n
xk=r1ku1+⋯+rkkuk+0⋅uk+1+⋯+0⋅un
于是
x
k
=
Q
r
k
\mathbf x_k=Q\mathbf r_k
xk=Qrk
其中
r
k
=
(
r
1
k
,
⋯
,
r
k
k
,
0
,
⋯
,
0
)
T
\mathbf r_k=(r_{1k},\cdots,r_{kk},0,\cdots,0)^T
rk=(r1k,⋯,rkk,0,⋯,0)T ,且
r
k
k
⩾
0
r_{kk}\geqslant 0
rkk⩾0 (在正交化过程中,若
r
k
k
<
0
r_{kk}<0
rkk<0 ,则
r
k
k
r_{kk}
rkk 和
u
k
\mathbf u_k
uk 同乘-1)。取
R
=
(
r
1
,
r
2
,
⋯
,
r
n
)
R=(\mathbf r_1,\mathbf r_2,\cdots,\mathbf r_n)
R=(r1,r2,⋯,rn) ,则
A
=
(
Q
r
1
,
Q
r
2
,
⋯
,
Q
r
n
)
=
Q
R
A=(Q\mathbf r_1,Q\mathbf r_2,\cdots,Q\mathbf r_n)=QR
A=(Qr1,Qr2,⋯,Qrn)=QR
例:求
A
=
[
1
0
0
1
1
0
1
1
1
1
1
1
]
A=\begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix}
A=
111101110011
的一个 QR 分解
解:通过施密特正交化方法我们可以得到
col
A
\text{col }A
col A 的一组标准正交基,将这些向量组成矩阵
Q
=
[
1
/
2
−
3
/
12
0
1
/
2
1
/
12
−
2
/
6
1
/
2
1
/
12
1
/
6
1
/
2
1
/
12
1
/
6
]
Q=\begin{bmatrix}1/2&-3/\sqrt{12}&0\\1/2&1/\sqrt{12}&-2/\sqrt{6}\\1/2&1/\sqrt{12}&1/\sqrt{6}\\1/2&1/\sqrt{12}&1/\sqrt{6}\end{bmatrix}
Q=
1/21/21/21/2−3/121/121/121/120−2/61/61/6
注意到
Q
Q
Q 是正交矩阵,
Q
T
=
Q
−
1
Q^T=Q^{-1}
QT=Q−1 。所以
R
=
Q
−
1
A
=
Q
T
A
R=Q^{-1}A=Q^TA
R=Q−1A=QTA
R
=
[
1
/
2
1
/
2
1
/
2
1
/
2
−
3
/
12
1
/
12
1
/
12
1
/
12
0
−
2
/
6
1
/
6
1
/
6
]
[
1
0
0
1
1
0
1
1
1
1
1
1
]
=
[
2
3
/
2
1
0
3
/
12
2
/
12
0
0
2
/
6
]
R=\begin{bmatrix}1/2&1/2&1/2&1/2\\ -3/\sqrt{12}&1/\sqrt{12}&1/\sqrt{12}&1/\sqrt{12} \\ 0&-2/\sqrt{6}&1/\sqrt{6}&1/\sqrt{6} \end{bmatrix} \begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix}= \begin{bmatrix}2&3/2&1\\0&3/\sqrt{12}&2/\sqrt{12}\\0&0&2/\sqrt{6} \end{bmatrix}
R=
1/2−3/1201/21/12−2/61/21/121/61/21/121/6
111101110011
=
2003/23/12012/122/6
特征值分解
特征值分解是将矩阵分解成特征值和特征向量形式:
A
=
Q
Σ
Q
−
1
A=Q\Sigma Q^{-1}
A=QΣQ−1
其中,
Σ
=
diag
(
λ
1
,
λ
2
,
⋯
,
λ
n
)
\Sigma=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_n)
Σ=diag(λ1,λ2,⋯,λn) 是一个对角阵,其对角线元素是矩阵
A
A
A 的特征值按降序排列
λ
1
⩾
λ
2
⩾
⋯
⩾
λ
n
\lambda_1\geqslant\lambda_2\geqslant\cdots\geqslant\lambda_n
λ1⩾λ2⩾⋯⩾λn,
Q
=
(
u
1
,
u
2
,
…
,
u
n
)
Q=(\mathbf u_1,\mathbf u_2,\dots,\mathbf u_n)
Q=(u1,u2,…,un) 是特征值对应的特征向量组成的矩阵。

特征值分解后,方阵的幂变得更容易计算
A
t
=
Q
Σ
t
Q
−
1
=
Q
[
λ
1
t
⋱
λ
n
t
]
Q
−
1
A^t=Q\Sigma^t Q^{-1}=Q\begin{bmatrix}\lambda_1^t\\&\ddots\\&&\lambda_n^t\end{bmatrix}Q^{-1}
At=QΣtQ−1=Q
λ1t⋱λnt
Q−1
特征值分解可以理解为:先切换基向量,然后伸缩变换,最后再切换回原来的基向量。其中,
Σ
\Sigma
Σ 中的特征向量描述伸缩变换的程度,特征向量描述变换的方向。
特征值分解有一定的局限性,因为它只适用于满秩的方阵。
例:求矩阵 A = [ − 2 1 1 0 2 0 − 4 1 3 ] A=\begin{bmatrix}-2&1&1\\0&2&0\\-4&1&3\end{bmatrix} A= −20−4121103 的特征值分解。
解:矩阵
A
A
A 的特征多项式为
det
(
A
−
λ
I
)
=
−
(
λ
−
2
)
2
(
λ
+
1
)
\det(A-\lambda I)=-(\lambda-2)^2(\lambda+1)
det(A−λI)=−(λ−2)2(λ+1) 。特征值和特征向量分别为
λ
1
=
−
1
:
u
1
=
[
1
0
1
]
;
λ
2
=
2
:
u
2
=
[
0
1
−
1
]
,
u
3
=
[
1
0
4
]
\lambda_1=-1:\mathbf u_1=\begin{bmatrix}1\\0\\1\end{bmatrix};\quad \lambda_2=2:\mathbf u_2=\begin{bmatrix}0\\1\\-1\end{bmatrix}, \mathbf u_3=\begin{bmatrix}1\\0\\4\end{bmatrix}
λ1=−1:u1=
101
;λ2=2:u2=
01−1
,u3=
104
可通过行变换计算逆矩阵
(
Q
,
I
)
=
[
0
1
1
1
0
0
1
0
0
0
1
0
−
1
4
1
0
0
1
]
→
[
1
0
0
0
1
0
0
1
0
−
1
/
3
1
/
3
1
/
3
0
0
1
4
/
3
−
1
/
3
−
1
/
3
]
=
(
I
,
Q
−
1
)
(Q,I)=\begin{bmatrix}\begin{array}{ccc:ccc} 0&1&1&1&0&0\\1&0&0&0&1&0\\-1&4&1&0&0&1 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{ccc:ccc} 1&0&0&0&1&0\\0&1&0&-1/3&1/3&1/3\\0&0&1&4/3&-1/3&-1/3 \end{array}\end{bmatrix}=(I,Q^{-1})
(Q,I)=
01−1104101100010001
→
1000100010−1/34/311/3−1/301/3−1/3
=(I,Q−1)
所以
A
=
[
0
1
1
1
0
0
−
1
4
1
]
[
2
0
0
0
2
0
0
0
−
1
]
[
0
1
0
−
1
/
3
1
/
3
1
/
3
4
/
3
−
1
/
3
−
1
/
3
]
A=\begin{bmatrix}0&1&1\\1&0&0\\-1&4&1\end{bmatrix} \begin{bmatrix}2&0&0\\0&2&0\\0&0&-1\end{bmatrix} \begin{bmatrix}0&1&0\\-1/3&1/3&1/3\\4/3&-1/3&-1/3\end{bmatrix}
A=
01−1104101
20002000−1
0−1/34/311/3−1/301/3−1/3
奇异值分解
奇异值分解
奇异值分解(Singular Value Decomposition, SVD)是线性代数中一种重要的矩阵分解,在生物信息学、信号处理、金融学、统计学等领域有重要应用。
SVD 可以理解为同一线性变换 T : R n ↦ R m T:\R^n\mapsto\R^m T:Rn↦Rm 在不同基下的矩阵表示。假设 Grant 选用标准基,对应的矩阵为 A m × n A_{m\times n} Am×n 。类似于特征值分解, Jennifer 通过选择合适的基向量,对应的矩阵变为简单的长方形对角矩阵 Σ m × n \Sigma_{m\times n} Σm×n,即只有伸缩变换。
假定 Jennifer 使用矩阵 V n = ( v 1 , ⋯ , v n ) V_n=(\mathbf v_1,\cdots,\mathbf v_n) Vn=(v1,⋯,vn) 的列向量作为 R n R^n Rn 的基,使用矩阵 U n = ( u 1 , ⋯ , u m ) U_n=(\mathbf u_1,\cdots,\mathbf u_m) Un=(u1,⋯,um)的列向量作为 R m R^m Rm 的基 。那么,对于 Jennifer 视角下的向量 x ∈ R n \mathbf x\in R^n x∈Rn
- 同样的向量,用 Grant 的坐标系表示为 V x V\mathbf x Vx
- 用 Grant 的语言描述变换后的向量 A V x AV\mathbf x AVx
- 将变换后的结果变回 Jennifer 的坐标系 U − 1 A V x U^{-1}AV\mathbf x U−1AVx
于是,我们得到同一个线性变换 T T T 在 Jennifer 的坐标系下对应的矩阵 Σ = U − 1 A V \Sigma=U^{-1}AV Σ=U−1AV ,也可理解为矩阵 A A A 分解为 A m × n = U m Σ m × n V n − 1 A_{m\times n}=U_m\Sigma_{m\times n}V^{-1}_n Am×n=UmΣm×nVn−1 。
接下来,自然是探讨上述矩阵分解的适用条件。
注意到
A
T
A
=
(
U
Σ
V
−
1
)
T
(
U
Σ
V
−
1
)
=
V
−
T
Σ
T
U
T
U
Σ
V
−
1
A^TA=(U\Sigma V^{-1})^T(U\Sigma V^{-1})=V^{-T}\Sigma^TU^TU\Sigma V^{-1}
ATA=(UΣV−1)T(UΣV−1)=V−TΣTUTUΣV−1
不妨取
U
,
V
U,V
U,V 为单位正交基,即
U
,
V
U,V
U,V 为正交矩阵
U
T
U
=
I
,
V
T
V
=
I
U^TU=I,V^TV=I
UTU=I,VTV=I ,则
A
T
A
=
V
Σ
T
Σ
V
T
A^TA=V\Sigma^T\Sigma V^T
ATA=VΣTΣVT
于是,可知
V
V
V 的列向量为
A
T
A
A^TA
ATA 的特征向量,
Σ
T
Σ
\Sigma^T\Sigma
ΣTΣ 为
n
n
n 阶对角阵,其对角元素为
A
T
A
A^TA
ATA 的特征值。事实上
A
T
A
A^TA
ATA 为对称阵,必定存在正交矩阵
V
V
V 相似对角化。
同理
A
A
T
=
U
Σ
Σ
T
U
T
AA^T=U\Sigma\Sigma^T U^T
AAT=UΣΣTUT
可知
U
U
U 的列向量为
A
A
T
AA^T
AAT 的特征向量,
Σ
Σ
T
\Sigma\Sigma^T
ΣΣT 为
m
m
m 阶对角阵,其对角元素为
A
A
T
AA^T
AAT 的特征值。矩阵
A
T
A
A^TA
ATA 为对称阵,必定存在正交矩阵
U
U
U 相似对角化。
目前 U , V U,V U,V 我们都求出来了,只剩下求出长方形对角矩阵 Σ \Sigma Σ 。根据 Sylvester降幂公式, A T A A^TA ATA 和 A A T AA^T AAT 有相同的非零特征值。
令
Σ
=
[
Λ
r
O
O
O
]
\Sigma=\begin{bmatrix}\Lambda_r&O\\O&O\end{bmatrix}
Σ=[ΛrOOO] ,其中
Λ
r
=
diag
(
σ
1
,
⋯
,
σ
r
)
\Lambda_r=\text{diag}(\sigma_1,\cdots,\sigma_r)
Λr=diag(σ1,⋯,σr) 。则
Σ
T
Σ
=
[
Λ
r
2
O
O
O
]
n
,
Σ
Σ
T
=
[
Λ
r
2
O
O
O
]
m
\Sigma^T\Sigma=\begin{bmatrix}\Lambda_r^2&O\\O&O\end{bmatrix}_n,\quad \Sigma\Sigma^T=\begin{bmatrix}\Lambda_r^2&O\\O&O\end{bmatrix}_m
ΣTΣ=[Λr2OOO]n,ΣΣT=[Λr2OOO]m
其中
Λ
r
2
=
diag
(
σ
1
2
,
⋯
,
σ
r
2
)
\Lambda_r^2=\text{diag}(\sigma_1^2,\cdots,\sigma_r^2)
Λr2=diag(σ12,⋯,σr2) 。因此,矩阵
Σ
\Sigma
Σ 的对角元素是
A
T
A
A^TA
ATA 和
A
A
T
AA^T
AAT 的特征值
λ
j
\lambda_j
λj 的平方根
σ
j
=
λ
j
\sigma_j=\sqrt{\lambda_j}
σj=λj
综上,任意矩阵均可奇异值分解。

定义:SVD是指将秩为
r
r
r 的
m
×
n
m\times n
m×n 矩阵
A
A
A分解为
A
=
U
Σ
V
T
A=U\Sigma V^T
A=UΣVT
其中 U U U 为 m m m 阶正交阵, V V V 为 n n n 阶正交阵, Σ \Sigma Σ 为 m × n m\times n m×n 维长方形对角矩阵,对角元素称为矩阵 A A A 的奇异值,一般按降序排列 σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ r > 0 \sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_r>0 σ1⩾σ2⩾⋯⩾σr>0 ,这样 Σ \Sigma Σ 就唯一确定了。矩阵 U U U 的列向量称为左奇异向量(left singular vector),矩阵 V V V 的列向量称为右奇异向量(right singular vector)。
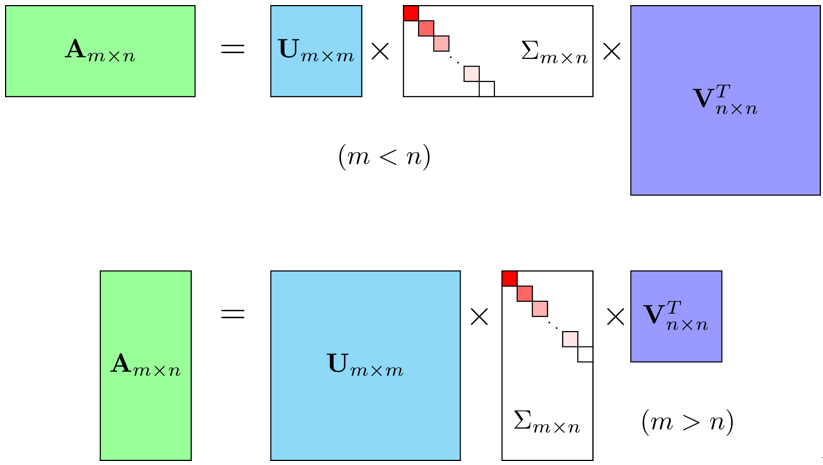
例:这里我们用一个简单的矩阵来说明奇异值分解的步骤。求矩阵 A = [ 0 1 1 1 1 0 ] A=\begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix} A= 011110 的奇异值分解
解:首先求出对称阵
A
T
A
A^TA
ATA 和
A
A
T
AA^T
AAT
A
T
A
=
[
0
1
1
1
1
0
]
[
0
1
1
1
1
0
]
=
[
2
1
1
2
]
A
A
T
=
[
0
1
1
1
1
0
]
[
0
1
1
1
1
0
]
=
[
1
1
0
1
2
1
0
1
1
]
A^TA=\begin{bmatrix}0&1&1\\1&1&0\end{bmatrix} \begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix}= \begin{bmatrix}2&1\\1&2\end{bmatrix} \\ AA^T=\begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix} \begin{bmatrix}0&1&1\\1&1&0\end{bmatrix}= \begin{bmatrix}1&1&0\\1&2&1\\0&1&1\end{bmatrix}
ATA=[011110]
011110
=[2112]AAT=
011110
[011110]=
110121011
然后求出
A
T
A
A^TA
ATA 的特征值和特征向量
λ
1
=
3
:
v
1
=
[
1
/
2
1
/
2
]
;
λ
2
=
1
:
v
2
=
[
−
1
/
2
1
/
2
]
\lambda_1=3:\mathbf v_1=\begin{bmatrix}1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix};\quad \lambda_2=1:\mathbf v_2=\begin{bmatrix}-1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix}
λ1=3:v1=[1/21/2];λ2=1:v2=[−1/21/2]
求出
A
A
T
AA^T
AAT 的特征值和特征向量
λ
1
=
3
:
u
1
=
[
1
/
6
2
/
6
1
/
6
]
;
λ
2
=
1
:
u
2
=
[
1
/
2
0
−
1
/
2
]
;
λ
3
=
0
:
u
3
=
[
1
/
3
−
1
/
3
1
/
3
]
;
\lambda_1=3:\mathbf u_1=\begin{bmatrix}1/\sqrt{6}\\2/\sqrt{6}\\1/\sqrt{6}\end{bmatrix};\quad \lambda_2=1:\mathbf u_2=\begin{bmatrix}1/\sqrt{2}\\0\\-1/\sqrt{2}\end{bmatrix};\quad \lambda_3=0:\mathbf u_3=\begin{bmatrix}1/\sqrt{3}\\-1/\sqrt{3}\\1/\sqrt{3}\end{bmatrix};
λ1=3:u1=
1/62/61/6
;λ2=1:u2=
1/20−1/2
;λ3=0:u3=
1/3−1/31/3
;
其次可以利用
σ
i
=
λ
i
\sigma_i=\sqrt{\lambda_i}
σi=λi 求出奇异值
3
,
1
\sqrt{3},1
3,1
最终得到
A
A
A的奇异值分解
A
=
U
Σ
V
T
=
[
1
/
6
1
/
2
1
/
3
2
/
6
0
−
1
/
3
1
/
6
−
1
/
2
1
/
3
]
[
3
0
0
1
0
0
]
[
1
/
2
1
/
2
−
1
/
2
1
/
2
]
A=U\Sigma V^T=\begin{bmatrix}1/\sqrt{6}&1/\sqrt{2}&1/\sqrt{3}\\2/\sqrt{6}&0&-1/\sqrt{3}\\1/\sqrt{6}&-1/\sqrt{2}&1/\sqrt{3}\end{bmatrix} \begin{bmatrix}\sqrt{3}&0\\0&1\\0&0\end{bmatrix} \begin{bmatrix}1/\sqrt{2}&1/\sqrt{2}\\-1/\sqrt{2}&1/\sqrt{2}\end{bmatrix}
A=UΣVT=
1/62/61/61/20−1/21/3−1/31/3
300010
[1/2−1/21/21/2]
矩阵的基本子空间
设矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT ,有 r r r 个不为零的奇异值,则可以得到矩阵 A A A 的四个基本子空间:
- 正交阵 U U U 的前 r r r 列是 col A \text{col }A col A 的一组单位正交基
- 正交阵 U U U 的后 m − r m-r m−r 列是 ker A T \ker A^T kerAT 的一组单位正交基
- 正交阵 V V V 的前 r r r 列是 col A T \text{col }A^T col AT 的一组单位正交基
- 正交阵 V V V 的后 n − r n-r n−r 列是 ker A \ker A kerA 的一组单位正交基
A ( v 1 , ⋯ , v r ⏟ col A T , v r + 1 ⋯ v n ⏟ ker A ) = ( u 1 , ⋯ , u r ⏟ col A , u r + 1 ⋯ u m ⏟ ker A T ) [ σ 1 ⋱ σ r O ] ⏟ Σ m × n A(\underbrace{\mathbf v_1,\cdots,\mathbf v_r}_{\text{col }A^T},\underbrace{\mathbf v_{r+1}\cdots\mathbf v_n}_{\ker A})= (\underbrace{\mathbf u_1,\cdots,\mathbf u_r}_{\text{col }A},\underbrace{\mathbf u_{r+1}\cdots\mathbf u_m}_{\ker A^T}) \underbrace{\begin{bmatrix}\sigma_1\\&\ddots\\&&\sigma_r\\&&&O \end{bmatrix}}_{\Sigma_{m\times n}} A(col AT v1,⋯,vr,kerA vr+1⋯vn)=(col A u1,⋯,ur,kerAT ur+1⋯um)Σm×n σ1⋱σrO
证:易知
A
V
=
U
Σ
AV=U\Sigma
AV=UΣ ,即
{
A
v
i
=
σ
i
u
i
,
1
⩽
i
⩽
r
A
v
i
=
0
,
r
<
i
⩽
n
\begin{cases} A\mathbf v_i=\sigma_i\mathbf u_i, &1\leqslant i\leqslant r \\ A\mathbf v_i=0, &r< i\leqslant n \end{cases}
{Avi=σiui,Avi=0,1⩽i⩽rr<i⩽n
取
v
1
,
⋯
,
v
n
\mathbf v_1,\cdots,\mathbf v_n
v1,⋯,vn 为
R
n
\R^n
Rn 的单位正交基,对于
∀
x
∈
R
n
\forall\mathbf x\in \R^n
∀x∈Rn ,可以写出
x
=
c
1
v
1
+
⋯
+
c
n
v
n
\mathbf x=c_1\mathbf v_1+\cdots+c_n\mathbf v_n
x=c1v1+⋯+cnvn,于是
A
x
=
c
1
A
v
1
+
⋯
+
c
r
A
v
r
+
c
r
+
1
A
v
r
+
1
+
⋯
+
c
n
v
n
=
c
1
σ
1
u
1
+
⋯
+
c
r
σ
1
u
r
+
0
+
⋯
+
0
\begin{aligned} A\mathbf x&=c_1A\mathbf v_1+\cdots+c_rA\mathbf v_r+c_{r+1}A\mathbf v_{r+1}+\cdots+c_n\mathbf v_n \\ &=c_1\sigma_1\mathbf u_1+\cdots+c_r\sigma_1\mathbf u_r+0+\cdots+0 \end{aligned}
Ax=c1Av1+⋯+crAvr+cr+1Avr+1+⋯+cnvn=c1σ1u1+⋯+crσ1ur+0+⋯+0
所以
A
x
∈
span
{
u
1
,
⋯
,
u
r
}
A\mathbf x\in\text{span}\{\mathbf u_1,\cdots,\mathbf u_r\}
Ax∈span{u1,⋯,ur} ,这说明矩阵
U
U
U 的前
r
r
r 列是
col
A
\text{col }A
col A 的一组单位正交基,因此
rank
A
=
r
\text{rank }A=r
rank A=r 。同时可知,对于任意的
x
∈
span
{
v
r
+
1
,
⋯
,
v
n
}
⟺
A
x
=
0
\mathbf x\in\text{span}\{\mathbf v_{r+1},\cdots,\mathbf v_n\}\iff A\mathbf x=0
x∈span{vr+1,⋯,vn}⟺Ax=0 ,于是
V
V
V 的后
n
−
r
n-r
n−r 列是
ker
A
\ker A
kerA 的一组单位正交基。
同样通过 A T U = V Σ A^TU=V\Sigma ATU=VΣ 可说明 V V V 的前 r r r 列是 col A T \text{col }A^T col AT 的一组单位正交基, U U U 的后 m − r m-r m−r 列是 ker A T \ker A^T kerAT 的一组单位正交基。
奇异值分解的性质
设矩阵
A
=
U
Σ
V
T
A=U\Sigma V^T
A=UΣVT ,秩
rank
A
=
r
\text{rank }A=r
rank A=r ,分别将
U
,
Σ
,
V
U,\Sigma,V
U,Σ,V 进行分块
U
=
(
U
r
,
U
m
−
r
)
V
=
(
V
r
,
V
n
−
r
)
Σ
=
[
Λ
r
O
O
O
]
U=(U_r,U_{m-r}) \\ V=(V_r,V_{n-r}) \\ \Sigma=\begin{bmatrix}\Lambda_r&O\\O&O\end{bmatrix}
U=(Ur,Um−r)V=(Vr,Vn−r)Σ=[ΛrOOO]
其中
U
r
=
(
u
1
,
⋯
,
u
r
)
U_r=(\mathbf u_1,\cdots,\mathbf u_r)
Ur=(u1,⋯,ur) 为
m
×
r
m\times r
m×r维矩阵,
V
r
=
(
v
1
,
⋯
,
v
r
)
V_r=(\mathbf v_1,\cdots,\mathbf v_r)
Vr=(v1,⋯,vr) 为
n
×
r
n\times r
n×r维矩阵,
Λ
r
=
diag
(
σ
1
,
⋯
,
σ
r
)
\Lambda_r=\text{diag}(\sigma_1,\cdots,\sigma_r)
Λr=diag(σ1,⋯,σr) 为
r
r
r 阶对角阵。应用矩阵乘法的性质,奇异值分解可以简化为
A
=
U
r
Λ
r
V
r
T
A=U_r\Lambda_r V^T_r
A=UrΛrVrT
这个分解称为简化奇异值分解。
性质:
- 奇异值分解可理解为将线性变换分解为三个简单的变换:正交变换 V T V^T VT,伸缩变换 Σ \Sigma Σ 和正交变换 U U U 。
- 矩阵 A A A 的奇异值分解中,奇异值是唯一的,但矩阵 U , V U,V U,V 不是唯一的。
- 令
λ
\lambda
λ 为
A
T
A
A^TA
ATA 的一个特征值,
v
\mathbf v
v 是对应的特征向量,则
∥ A v ∥ 2 = v T A T A v = λ v T v = λ ∥ v ∥ \|A\mathbf v\|^2=\mathbf v^TA^TA\mathbf v=\lambda\mathbf v^T\mathbf v=\lambda\|\mathbf v\| ∥Av∥2=vTATAv=λvTv=λ∥v∥ - 易知
A
V
=
U
Σ
AV=U\Sigma
AV=UΣ 或
A
T
U
=
V
Σ
T
A^TU=V\Sigma^T
ATU=VΣT,则左奇异向量和右奇异向量存在关系
A v j = σ j u j A T u j = σ j v j A\mathbf v_j=\sigma_j\mathbf u_j \\ A^T\mathbf u_j=\sigma_j\mathbf v_j Avj=σjujATuj=σjvj
矩阵的外积展开式
矩阵
A
=
U
Σ
V
T
A=U\Sigma V^T
A=UΣVT 可展开为若干个秩为1的
m
×
n
m\times n
m×n矩阵之和
A
=
σ
1
u
1
v
1
T
+
σ
2
u
2
v
2
T
+
⋯
+
σ
r
u
r
v
r
T
A=\sigma_1\mathbf u_1\mathbf v_1^T+\sigma_2\mathbf u_2\mathbf v_2^T+\cdots+\sigma_r\mathbf u_r\mathbf v_r^T
A=σ1u1v1T+σ2u2v2T+⋯+σrurvrT
上式称为矩阵 A A A 的外积展开式。
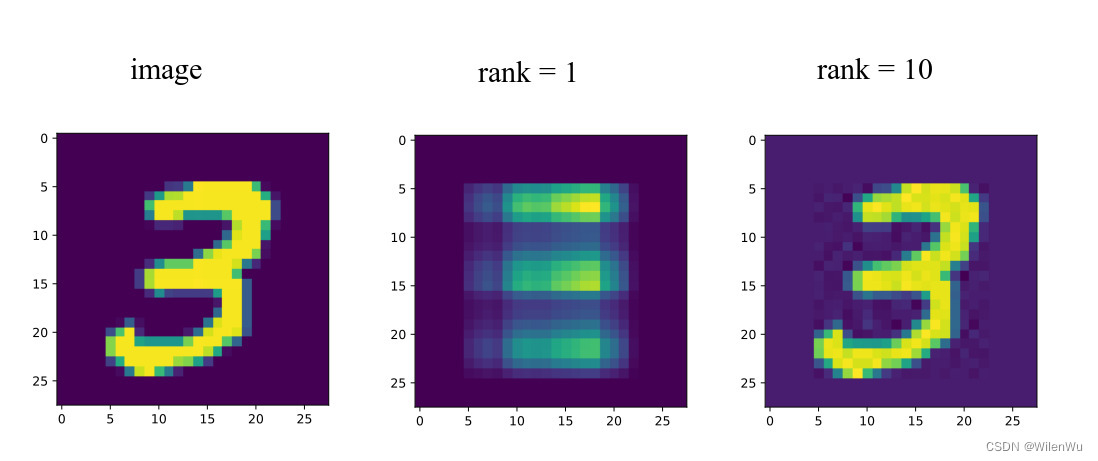
在长方形对角矩阵 Σ \Sigma Σ 中奇异值按从大到小的顺序排列 σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ r > 0 \sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_r>0 σ1⩾σ2⩾⋯⩾σr>0 。在很多情况下,由于奇异值递减很快,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上。因此,我们可以用前面 k k k 个大的奇异值来近似描述矩阵。
奇异值分解也是一种矩阵近似的方法,这个近似是在矩阵范数意义下的近似。矩阵范数是向量范数的直接推广。
∥
A
∥
2
=
(
∑
j
=
1
n
∑
i
=
1
m
∣
a
i
j
∣
2
)
1
/
2
\|A\|_2=(\sum_{j=1}^{n}\sum_{i=1}^{m} |a_{ij}|^2)^{1/2}
∥A∥2=(j=1∑ni=1∑m∣aij∣2)1/2
可以证明
∥
A
∥
2
2
=
tr
(
A
T
A
)
=
∑
i
=
1
r
σ
i
2
\|A\|_2^2=\text{tr}(A^TA)= \sum_{i=1}^{r} \sigma_i^2
∥A∥22=tr(ATA)=i=1∑rσi2
设矩阵
A
k
=
∑
i
=
1
k
σ
i
u
i
v
i
T
A_k=\sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i^T
Ak=i=1∑kσiuiviT
则
A
k
A_k
Ak 的秩为
k
k
k ,矩阵
A
k
A_k
Ak 称为
A
A
A 的截断奇异值分解。并且
A
k
A_k
Ak 是秩为
k
k
k 时的最优近似,即
A
k
A_k
Ak 为以下最优问题的解
min
∥
A
−
X
∥
2
s.t. rank
A
=
k
\min\|A-X\|_2 \\ \text{s.t. rank }A=k
min∥A−X∥2s.t. rank A=k
上式称为低秩近似(low-rank approximation)。于是奇异值分解可近似为
A
≈
∑
i
=
1
k
σ
i
u
i
v
i
T
=
U
m
×
k
Σ
k
×
k
V
n
×
k
T
A\approx \sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i^T=U_{m\times k}\Sigma_{k\times k}V_{n\times k}^T
A≈i=1∑kσiuiviT=Um×kΣk×kVn×kT
其中 k k k 是一个远远小于 m m m和 n n n的数,从计算机内存的角度来说,矩阵左(右)奇异向量和奇异值的存储要远远小于矩阵 A A A的。所以,截断奇异值分解就是在计算精度和时间空间之间做选择。如果 k k k越大,右边的三个矩阵相乘的结果越接近于 A A A。
截断奇异值分解常用于图像压缩,如下图