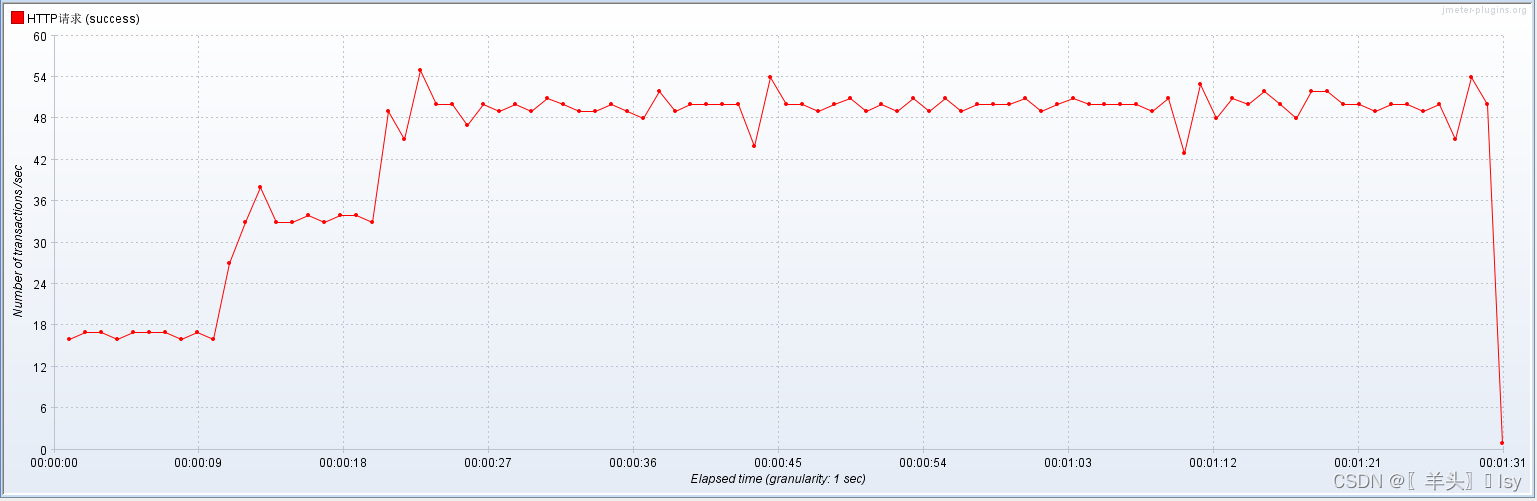
力扣215题， 给定整数数组nums和整数k，请返回数组中第k个最大的元素。 请注意，你需要找的是数组排序后的第k个最大的元素，而不是第k个不同的元素。

分析：按照“找最大用小堆，找最小用大堆，找中间用两个堆”，这道题用最小堆来解决，构造一个大小只有K的最小堆。举个例子，序列[2, 4, 1, 3, 2, 5, 3, 6, 6, 9],比如找第4大的数，先让前四个入堆，之后继续遍历与堆顶元素进行比较，比堆顶元素大才能入堆否则不行。

新元素的插入只是替换根元素，然后重新构造最小堆，完成之后的根元素就是第4大的元素。

代码如下：

function findKthLargest(nums, k) {
	let heapSize = nums.length;
	buildMaxHeap(nums, heapSize); // 构建好一个大顶堆
	// 进行下沉，大顶堆是最大元素下沉到末尾
	for (let i = nums.length - 1; i >= nums.length - k + 1; i--) {
		swap(nums, 0, i);
		// 下沉后的元素不参与到大顶堆的调整
		--heapSize;
		// 重新调整大顶堆
		maxHeapify(nums, 0, heapSize);
	}
	return nums[0]

	// 自上而下构建一颗大顶堆
	function buildMaxHeap(nums, heapSize) {
		for (let i = Math.floor(heapSize / 2) - 1; i >= 0; i--) {
			maxHeapify(nums, i, heapSize);
		}
	}

	// 从左向右，自上而下的调整节点
	function maxHeapify(nums, i, heapSize) {
		let left = i*2 + 1;
		let right = i*2 + 2;
		let largest = i;
		if (left < heapSize && nums[left] > nums[largest]) {
			largest = left;
		}
		if (right < heapSize && nums[right] > nums[largest]) {
			largest = right;
		}
		if (largest !== i) {
			// 进行节点调整
			swap(nums, i, largest); 
			// 继续调整下面的非叶子节点
			maxHeapify(nums, largest, heapSize);
		}
	}

	function swap(arr, i, j) {
		let temp = a[i];
		a[i] = a[j];
		a[j] = temp;
	}

}

参考：落落落洛克