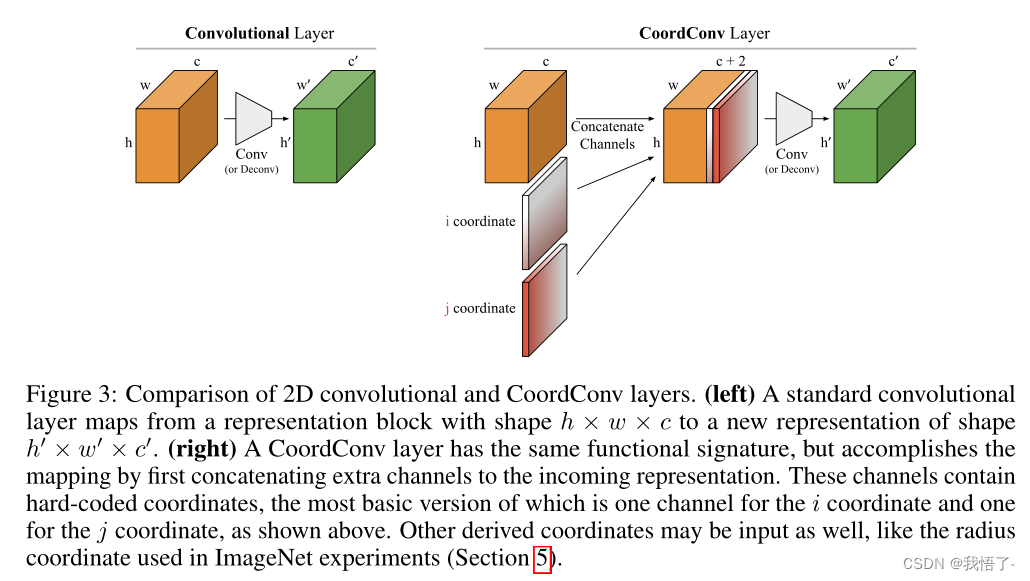
Reflective Shadow Maps（RSM）

一切被直接光照照到的物体，会作为次级光源。

问题1：哪些面片被直接照亮

使用ShadowMap就可以知道哪些面片被直接照亮

问题2：各个面片对P点的贡献分别是多少。

对渲染方程代入如上计算，得到如下结果

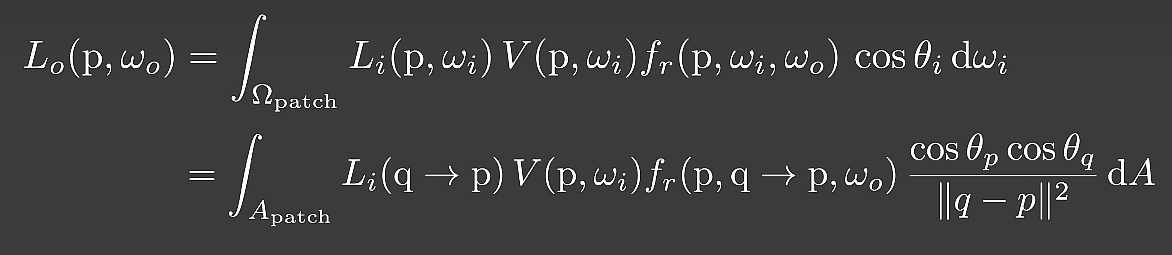
在上式中，$L_i(q\to p)$可优化为如下函数
因为：
$$\begin{gathered} f_r=\rho /\pi ，\rho 为反射率 \\ {L}_i=f_r\cdot \frac{\varphi }{dA}，\varphi 是直接光照的光强 \end{gathered}$$
因此有次级光源光强
E p ( x , n ) = ϕ p m a x { 0 , d o t ( n p , ( x − x p ) } m a x { 0 , d o t ( n , x p − x ) } ∣ ∣ x − x p ∣ ∣ 4 E_p(x,n)=\phi_p \frac{max\{0,dot(n_p,(x-x_p)\}max\{0,dot(n,x_p-x)\}}{||x-x_p||^4} Ep​(x,n)=ϕp​∣∣x−xp​∣∣4max{0,dot(np​,(x−xp​)}max{0,dot(n,xp​−x)}​

$$L_0=E_p(x,n)\ast f_r(p,p\to q,w_o)$$

其他近似

1. 不考虑Visbility项，认为次级光源不会被遮挡。
2. 不对所有次级光源采样，只对该点在ShadowMap中周围的部分像素采样。

ShadowMap记录值

1. 深度
2. 世界坐标
3. 法线
4. 次级光源强度$\varphi$

特点与效果

对于特定情况效果比较好，如手电筒（用RSM做手电筒！！！？）
好处：非常好写，第一个Path生成RSM，第二个path用眼睛看向场景。
问题：

1. 直接光源较多时，间接光源也会成倍增多
2. 不会计算反射光的可见性检查
3. 次级光源效果和运行速度，会根据采样率的不同的不同

如何实现

第一步，先找到哪些物体表面能够被直接照亮，使用ShadowMap，认为每一个ShadowMap的像素就是一个次级光源。
第二步，次级光源如何贡献到点P：我们认为所有的反射物(次级光源)，都是Diffuse的。

RSM与VPL(Virtual Point Light 虚拟点光源)

RSM与离线渲染中的VPL方式是比较相似的，RSM是硬件加速版本的VPL(Virtual Point Light 虚拟点光源)。

RSM实现步骤

第一个Pass

在摄像机视角渲染整个场景，并记录场景中可见的像素点的颜色、视口矩阵下的法线、视口矩阵下的坐标。

得到一组场景信息，可以理解为GBuffer。

第2个Pass

从光源视口下看向场景，生成RSM图。
记录的从光源视口下可见像素点的反射光颜色值、相机视角下的法线、相机视角下的坐标、光源视角下的坐标。
得到的结果是一组256x256的RSM图

············反射光颜色值 ······························· 相机视角下的法线 ··················

··········· 相机视角下的坐标 ·························· 光源视角下的坐标（主要保存z轴深度）·······························

第3个Pass

1.将Pass1中保存的像素坐标转化到与RSM相同的光源坐标

	ivec2 FragPos = ivec2(gl_GlobalInvocationID.xy);//当前执行单元在全局工作组中的位置的有效索引
	vec3 FragViewNormal = normalize(texelFetch(u_NormalTexture, FragPos, 0).xyz);
	vec3 FragAlbedo = texelFetch(u_AlbedoTexture, FragPos, 0).xyz;
	vec3 FragViewPos = texelFetch(u_PositionTexture, FragPos, 0).xyz;

	// 获取 摄像机视口下像素 在光源视口下的位置坐标
	vec4 FragPosInLightSpace = u_LightVPMatrixMulInverseCameraViewMatrix * vec4(FragViewPos, 1);
	FragPosInLightSpace /= FragPosInLightSpace.w;
	vec2 FragNDCPos4Light = (FragPosInLightSpace.xy + 1) / 2;

2. 计算该像素点的直接光照

如果该像素点在光照空间外，则只提供一个基本的环境光照。
当该像素在光照空间内，首先判断该点是否在阴影中

• 如果在阴影中，则只计算环境光照
• 如果不在阴影中，则计算直接光照

// 直接光照&环境光照
	vec3 testOutput;
	vec3 DirectIllumination;
	// 如果该像素在RSM范围之外，以0.1倍源像素作为其环境光照
	// FragPosInLightSpace.z范围在【-1，0】的区间中.属于可被光照直接照射的范围
	// 这里可通过与RSM中的深度进行比较，来确定是否有阴影生成，或是否可被作为次级光源
	if(	FragPosInLightSpace.z < -1.0f || FragPosInLightSpace.z > 0.0f||\
		FragPosInLightSpace.x >=  1.0f || FragPosInLightSpace.x <= -1.0f||\
		FragPosInLightSpace.y >=  1.0f || FragPosInLightSpace.y <= -1.0f )//
	{
		DirectIllumination = vec3(0.1) * FragAlbedo;
		testOutput = vec3(0.f,0.f,0.f);
	}
	else//反之，将原像素经过夹角衰减后的值作为直接光照
	{	
		// view space下的光照坐标
		vec3 RSWLightPosition =texture(u_RSMLightPositionTexture,FragNDCPos4Light.xy).xyz;
		
		// 判断是否在阴影中(近小【-1】远大【0】)
		if(RSWLightPosition.z + 0.001 > FragPosInLightSpace.z){//不在阴影中
			DirectIllumination = FragAlbedo* max(dot(-u_LightDirInViewSpace, FragViewNormal), 0.1);// ;
		}
		else{//在阴影中
		   DirectIllumination = vec3(0.1) * FragAlbedo;
		}
	}

3. 计算该像素点的间接光照

将该着色点投影到光照视口下的点，则已知该点在RSM纹理上的xy轴位置。

在RSM图中，在（x,y）像素上以R为半斤的周围进行随机采样，每一个采样点作为次级光源进行光照计算。

// 计算间接光照
	vec3 IndirectIllumination = vec3(0);
	float RSMTexelSize = 1.0 / u_RSMSize;
	for(int i = 0; i < u_VPLNum; ++i)
	{
		if(FragPosInLightSpace.z > -1.0f && FragPosInLightSpace.z <0.0f){
			//获取随机采样数组
			vec3 VPLSampleCoordAndWeight = u_VPLsSampleCoordsAndWeights[i].xyz;
			// 在光源视口下的该像素点周围一圈进行采样
			vec2 VPLSamplePos = FragNDCPos4Light + u_MaxSampleRadius * VPLSampleCoordAndWeight.xy * RSMTexelSize;
			// 在RSM图中获取采样点的次级光源颜色值
			vec3 VPLFlux = texture(u_RSMFluxTexture, VPLSamplePos).xyz;
			// 获取采样点在摄像机视口坐标下的的法线和位置坐标
			vec3 VPLNormalInViewSpace = normalize(texture(u_RSMNormalTexture, VPLSamplePos).xyz);
			vec3 VPLPositionInViewSpace = texture(u_RSMPositionTexture, VPLSamplePos).xyz;
			// 计算该采样点对该像素的间接光照值
			IndirectIllumination += calcVPLIrradiance(VPLFlux, VPLNormalInViewSpace, VPLPositionInViewSpace, FragViewPos, FragViewNormal, VPLSampleCoordAndWeight.z);
		}
	}
	IndirectIllumination *= FragAlbedo;

	//间接光
	vec3 Result = IndirectIllumination / u_VPLNum;

4. 将直接光照与间接光照加起来

得到结果，渲染！

vec3 Result = DirectIllumination  + IndirectIllumination / u_VPLNum ;

区别【好像没太大区别 dog.jpg】